Уравновешивание вращающихся масс, расположенных произвольно
Последовательность уравновешивания масс, расположенных произвольно, рассмотрим на примере ротора с системой четырех неуравновешенных масс (рис. 6.3). Пусть известны величины неуравновешенных масс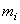 
и их положения относительно оси вращения ротора, обусловленные радиусами – векторами 
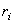и расстояниями 
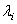относительно одной из произвольно выбранных плоскостей I, перпендикулярной оси вращения рассматриваемого ротора.
При вращении ротора и неуравновешенных масс с постоянной угловой скоростью на каждую из масс действует сила инерции
.
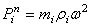Так как угловая скорость в рассматриваемом здесь частном случае является величиной постоянной, то угловое ускорение отсутствует (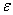 
= 0) и тангенциальная составляющая силы инерции равна нулю.
а) б)
в) г)
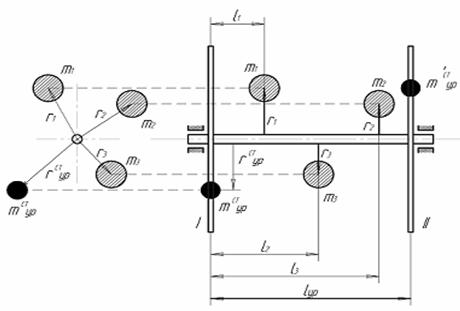
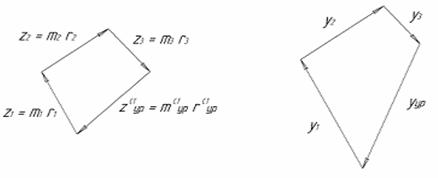
Рис. 6.3. Уравновешивание масс, расположенных произвольно:
а – вид на ротор с торца; б – вид на ротор с боку;
в – план сил при статическом уравновешивании;
г – план моментов сил при динамическом уравновешивании
Выбираем плоскости приведения I и II (см. рис. 6.3), в которых будем располагать уравновешивающие массы.
Задача заключается в том, что необходимо уравновесить массы динамически.
Сначала проводим статическое уравновешивание в плоскости I. Его последовательность описана в предыдущей главе.
, 
,
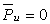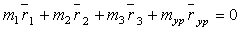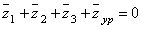. (7)
Используя (7), построим векторный многоугольник и графически найдем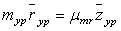 
.
Уравновесим действие инерционных моментов, т.е. выполним условие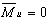 
. Для этого запишем уравнения
, 
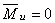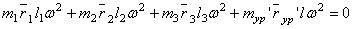. (8)
Так как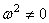 
, то из уравнения (8) следует, что
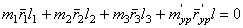. (9)
Решая графически векторное уравнение (9), находим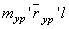 
.
Предварительно выбираем масштаб
.
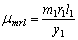Тогда уравнение (9) запишется в виде
.
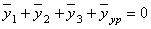При этом принимаем, что векторы моментов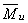 
повернуты на 900 и совпадают с направлением 
.
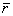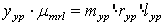. (10)
Находим из (10) величину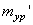 
, задавшись 
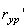, или наоборот. Здесь 
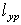равна расстоянию между плоскостями приведения I и II.
Проводя от оси вращения ротора линию, параллельную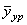 
, откладываем на ней с противоположных сторон 
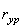и на концах этих векторов устанавливаем две уравновешивающие массы 
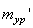. Причем одна из них будет расположена в плоскости I, другая – в плоскости II. Массы 
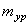и 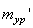в плоскости I можно объединить в одну массу.
Балансировка вращающихся масс (роторов)
Уравновешивание роторов или систем масс используется при проектировании механизмов.
В уже изготовленных роторах встречаются, как было сказано выше, неоднородности материала, возникают неточности изготовления и сборки, в результате чего возникает остаточная неуравновешенность, которую нужно устранять балансировкой.
Различают балансировку:
– статическую, которую производят для достаточно плоских роторов типа дисков, колес, маховиков, шкивов. Ротор при этом устанавливают в опорах с малым трением (например, на призмах) и путем добавления масс или высверливания добиваются безразличного положения балансируемогоротора на опорах;
– динамическую, которую выполняют для роторов, имеющих значительную длину (валы, широкие колеса, шкивы и т.д.), на специальных станках.
Задача балансировки ротора заключается в определении, в выбранных плоскостях коррекции, значений и углов дисбалансов и размещении в этих плоскостях корректирующих масс, дисбалансы которых равны по величине и противоположны по направлению найденным дисбалансам ротора. На практике балансировку проводят: при конструировании - расчетными методами, в процессе изготовления деталей и узлов - экспериментально на специальных балансировочных станках. Балансировка на станках является более точным и надежным методом, по сравнению с расчетными. Поэтому она применяется для ответственных деталей с высокими рабочими частотами вращения. Корректировка масс ротора осуществляется либо присоединением к нему дополнительных корректирующих масс (наплавлением, наваркой или привинчиванием противовесов), либо удалением части массы ротора с “тяжелой” стороны (фрезерованием или высверливанием). Точность балансировки характеризуется величиной остаточного дисбаланса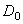 
ротора в каждой из плоскостей коррекции. Величина 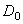не должна превышать допустимых для данного класса точности значений, регламентируемых ГОСТ 22061-76.
Балансировка эквивалентна уравновешиванию системы инерционных сил, прикладываемых к подвижному ротору для его равновесия.Эту систему, как и любую произвольную систему сил, можно заменить равнодействующими - главным вектором и главным моментом или двумя векторами, расположенными в произвольных параллельных плоскостях. Для уравновешивания системы сил достаточно уравновесить эти равнодействующие. При балансировке операции над силами заменяют действиями над дисбалансами. Поэтому для жестких роторов вышесказанное можно сформулировать так: жесткий ротор можно уравновесить двумя корректирующими массами, расположенными в двух произвольно выбранных плоскостях, перпендикулярных оси его вращения. Эти плоскости называют плоскостями коррекции.
Уравновешивание механизмов
Целью уравновешивания механизмов является устранение переменных во времени и пространстве воздействий стойки, станины механизма на опору, фундамент, вызывающих колебания фундамента и здания, а также уменьшение вибрации.