Применение отношений для обработки данных

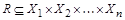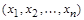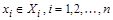Отношение может быть не только бинарным, в общем случае отношением называется подмножество , т.е. элементом отношения является упорядоченный набор , где . При обработке данных наборы из n элементов называют записями, i-му элементу набора соответствует i-ое поле записи. Записи группируются в файлы, и если файлы содержат совокупность записей, удовлетворяющих некоторым отношениям, мы получаем базу данных. Таким образом, отношение удобно представлять в виде таблицы, каждая строка которой соответствует записи, а каждый столбец – определенному полю записи.

Любая ли таблица может задавать отношение? Очевидными являются следующие требования:

1) порядок столбцов таблицы фиксирован;

2) каждый столбец имеет название;

3) порядок строк таблицы произволен;

4) в таблице нет одинаковых строк.

Число n столбцов таблицы называется степенью отношения (говорят, что задано n-арное отношение). Число строк в таблице – количество элементов отношения. Математическая модель, описывающая работу с такими таблицами, называется реляционной алгеброй.

1.3.2. Теоретико-множественные операции реляционной алгебры

Так как отношения являются множествами, к ним применимы обычные операции теории множеств: пересечение, объединение, разность. Но в отличие от алгебры множеств в реляционной алгебре эти операции могут быть применены не к любым, а только к совместимым отношениям. Два отношения будем называть совместимыми, если их степени равны, а соответствующие поля относятся к однотипным множествам. Первое требование означает, что объединение, пересечение и разность определяются только для таблиц с одинаковым количеством столбцов, а второе – в соответствующих столбцах должны располагаться однотипные данные (не выполняется операция пересечения множества фамилий и множества зарплат).

Пересечением двух отношений R и S называется множество 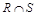всех записей, каждая из которых принадлежит как R, так и S (рис. 1.14, а, б).

Объединением двух отношений R и S называется множество 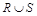записей, которые принадлежат хотя бы одному из отношений R или S (рис.1.14, а, в).

Разностью двух отношений R и S называется множество 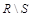всех записей, каждая из которых принадлежит отношению R, но не принадлежит отношению S (рис.1.14, а,г).

	R       S     A1 A2 A3 B1 B2 B3 a b a a b c b a c b c a b c a а) R Ç S R È S R \ S C1 C2 C2 D1 D2 D3 E1 E2 E3 b c a a b a a b a b a c b a c b c a a b c б) в) г) Рис. 1.14. Операции над совместимыми отношениями а) данные отношения R и S; б) пересечение отношений R и S; в) объединение отношений R и S; г) разность отношений R и S

В реляционной алгебре вводится операция расширенного декартова произведения. Пусть 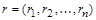– элемент n-арного отношения R, а 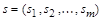– элемент m-арного отношения S. Конкатенацией записей r и s назовем запись 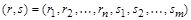, полученную приписыванием записи s к концу записи r.

	R   S   R ´ S A1 A2 B1 B2 B3 C1 C2 C3 C4 C5 a b k l m a b k l m a c b k c a b b k c c e a c k l m a c b k c c e k l m c e b k c Рис. 1.15. Расширенное декартово произведение отношений R и S

Расширенным декартовым произведением отношенийRиS называется множество 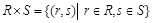, элементами которого являются все возможные конкатенации записе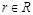й и 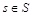. Отметим, что полученное отношение имеет степень 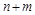и важен порядок выполнения операции: .

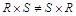В качестве упражнения запишите расширенное декартово произведение 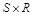для отношений R и S (рис. 1.15) и сравните с отношением .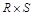