Множества, операции над ними.
ПРЯМЫЕ ПРОИЗВЕДЕНИЯ МНОЖЕСТВ
Вопросы
1. Что такое множество.
2. Как задаются множества
3. Что такое пустое множество
4. Что такое универсальное множество.
5. Как определяется мощность множества.
6. Какое множество называется счетным.
7. Какое множество называется континуальным.
8. Как определяется объединение множеств.
9. Как определяется пересечение множеств.
10. Что такое разность множеств.
11. Из каких элементов состоит множество 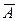 .
.
Задачи
1. Укажите смысловые связки естественного языка, соответствующие основным операциям над множествами: дополнение (– НЕ), объединение (сумма) (– ИЛИ), пересечение (произведение) (– И), разность (– БЕЗ).
2. Пусть 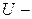 множество сотрудников некоторого предприятия;
множество сотрудников некоторого предприятия; 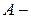 множество всех сотрудников старше 40 лет;
множество всех сотрудников старше 40 лет; 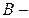 множество сотрудников, имеющих стаж более 10 лет;
множество сотрудников, имеющих стаж более 10 лет; 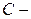 множество служащих;
множество служащих; 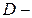 множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества.
множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества.
а) 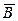 ; ; | д) 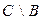 ; ; | и) 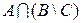 ; ; |
б) 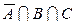 ; ; | е) 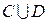 ; ; | к) 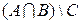 |
в) 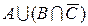 ; ; | ж) 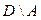 ; ; | л) 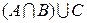 ; ; |
г) 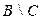 ; ; | з) 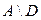 | м) 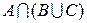 . . |
3. Заданы два множества: А = {1, 5, 7, 9, 12} и B = {5, 7, 9, 11, 13}. Найти множества 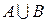 ;
; 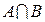 ;
; 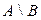 ;
; 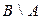 и их мощность.
и их мощность.
4. По заданным промежуткам А и B на числовой оси определить 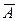 ;
; 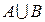 ;
; 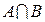 ;
; 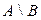 ;
; 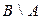 .
.
а) 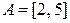 и
и 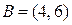 ; б)
; б) 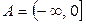 и
и 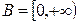 ;
;
в) 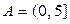 и
и 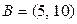 ; г)
; г) 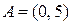 и
и 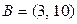
5. Построить из множества А, В и С результат операций над ними. А={1, 2, 3}, В={1, 3, 5}, С={2, 3, 4, 6}.
а) 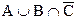 ; б)
; б) 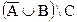 .
.
6. Пусть Множества А, В, С пересекаются в наиболее общем случае. Изобразить на диаграмме Эйлера Результат следующих действий:
а) 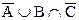 ; б)
; б) 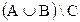 ; в)
; в) 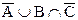 ; г)
; г) 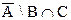 . 7. Пусть А и В – произвольные подмножества универсального множества U Доказать графически, что:
. 7. Пусть А и В – произвольные подмножества универсального множества U Доказать графически, что:
а) 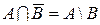 ; в)
; в) 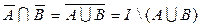 ;
;
б) 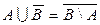 ; г)
; г) 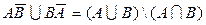 ;
;
д) 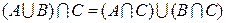 .
.
8. Пусть 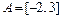 и
и 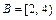 - промежутки на числовой оси. Найти
- промежутки на числовой оси. Найти 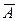 ;
; 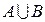 ;
; 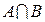 ;
; 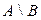 ;
; 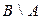 .
.
9.Определить мощности множеств 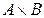 ;
; 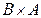 ;
; 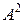 ;
; 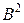 ;
; 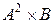 ;
; 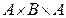 , и построить их, если
, и построить их, если
а) 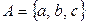 ;
; 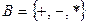 ; б)
; б) 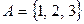 ;
; 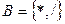 ;
;
в) 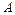 = {(1; 2)},
= {(1; 2)}, 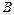 = {a; b; c; d}; г)
= {a; b; c; d}; г) 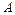 = {1; 2; 3},
= {1; 2; 3}, 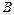 = {1; 2}.
= {1; 2}.
10. Пусть 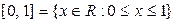 ;
; 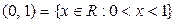 ;
; 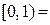
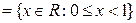 и
и 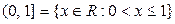 . Описать и изобразить графически следующие множества
. Описать и изобразить графически следующие множества
а) 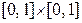 ; б)
; б) 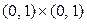 ; в)
; в) 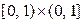 ; г)
; г) 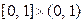 .
.
ВЕКТОРЫ. ОПЕРАЦИИ НАД НИМИ
Элементы пространства R 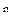 называются n-мерными векторами. Обозначаем:
называются n-мерными векторами. Обозначаем:  =(х
=(х  ,х
,х 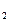 ,…х
,…х 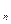 ), где
), где  (i=
(i= 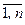 ) называются координаторами вектора
) называются координаторами вектора  , n – размерность вектора
, n – размерность вектора  .
.
Размерность можно обозначить так dim  = n.
= n.
Чтобы умножить вектор  = (х
= (х  , х
, х 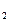 ,…х
,…х 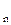 )на скаляр k, надо каждую координату вектора
)на скаляр k, надо каждую координату вектора  умножить на скаляр k.
умножить на скаляр k.
k 
 = (k
= (k  х
х  , k
, k  х
х 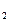 ,… k
,… k  х
х 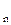 ).
).
Чтобы сложить два n-мерных вектора  =(х
=(х  , х
, х 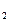 ,…х
,…х 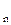 ) и
) и  = (у
= (у  ,у
,у  ,…,у
,…,у 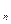 ), надо сложить соответствующие координаты.
), надо сложить соответствующие координаты.
 +
+  = (х
= (х  + у
+ у  , х
, х 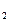 + у
+ у  , … х
, … х 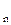 + у
+ у 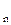 ).
).
Скалярным произведением векторов  и
и  называется число, находимое по формуле:
называется число, находимое по формуле:

 = х
= х  у
у  + х
+ х 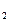 у
у  + … +х
+ … +х 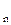 у
у 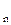 =
= 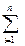 х
х 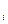 у
у 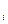 .
.
Свойства умножения вектора на скаляр и сложения векторов
1.  +
+  =
=  +
+  2. (
2. (  +
+  ) +
) + 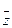 =
=  + (
+ (  +
+ 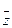 )
)
3. k  (
(  +
+  ) = k
) = k 
 + k
+ k  4. (k
4. (k  +k
+k  )
) 
 = k
= k 

 + k
+ k 


5. (k 
 k
k  )
) 
 = ( k
= ( k 

 )
)  k
k  = (k
= (k 

 )
)  k
k 
Свойства скалярного произведения векторов
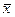
 =
= 
 ; 2.
; 2.  (
(  +
+ 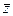 ) =
) = 
 +
+ 
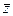 ; 3. k(
; 3. k( 
 )=(k
)=(k  )
)  =
=  (k
(k  )
)
Длинавектора  = (x
= (x  ,x
,x  ,…,x
,…,x 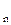 ) определяется формулой
) определяется формулой 
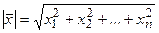
Расстояние между п-мерными точками (точками в R 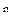 ) A(а
) A(а  ,а
,а  ,…,а
,…,а 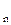 ) и B(b
) и B(b  , b
, b  ,…,b
,…,b 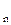 ) определяется формулой
) определяется формулой
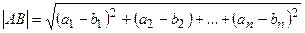
Косинус угла между п-мерными векторами 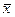 и
и  находится по формуле:
находится по формуле:
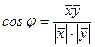 , где 0
, где 0 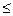 φ
φ 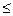 π.
π.
Примеры решения задач
Пример 1. Дана система векторов в R 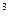 :
:
 = (1, 2, 4);
= (1, 2, 4);  = (0, 3, – 1);
= (0, 3, – 1);  = (3, 1, 2);
= (3, 1, 2); 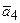 = (– 2, 0, – 1).
= (– 2, 0, – 1).
1. Найти линейные комбинации этих векторов.
а) 2  –
–  +
+  –
– 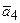 ; б)
; б)  + 2
+ 2  – 3
– 3  +
+ 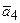 ; в) –
; в) –  –
–  –
–  –
– 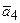 .
.
Решение:
а) 2 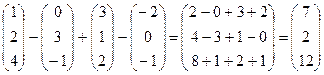 .
.
б) 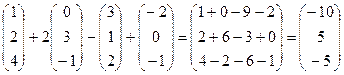 .
.
в) – 
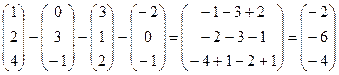 .
.
2. Найти значение выражения: 2(  +
+  ) – 3(
) – 3(  – 4
– 4  ).
).
Решение:
2(  +
+  ) – 3(
) – 3(  – 4
– 4  ) = 2
) = 2  + 2
+ 2 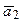 – 3
– 3  + 12
+ 12  = 2
= 2  –
–  + 12
+ 12  =
=
=2 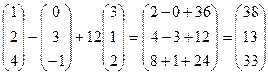 .
.
3. Найти скалярные произведения:

 ,
, 
 ,
, 
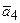 ,
, 
 ,
, 
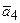 ,
, 
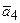 .
.
Решение:

 = 1
= 1  0 + 2
0 + 2  3 + 4
3 + 4  (–1) = 6 –4 = 2;
(–1) = 6 –4 = 2;

 = 1
= 1  3+2
3+2 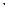 1+4
1+4  2 = 3 + 2 + 8 = 13;
2 = 3 + 2 + 8 = 13;

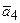 = 1
= 1  (–2) + 2
(–2) + 2  0 + 4
0 + 4  (–1) = –2 –4 = –6;
(–1) = –2 –4 = –6;

 = 0
= 0  3 + 3 1+ (–1)
3 + 3 1+ (–1)  2 = 3 –2 = 1;
2 = 3 –2 = 1;

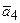 = 3
= 3  (–2) + 3
(–2) + 3  0 +(–1)
0 +(–1)  ( –1) = 1 ;
( –1) = 1 ;

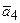 = 3
= 3  (–2) + 1
(–2) + 1  0 + 2
0 + 2  (–1) = –6 –2 = –8.
(–1) = –6 –2 = –8.
4. Найти длины векторов 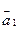 ,
, 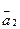 ,
, 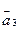 ,
, 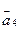 с точностью до 0,001.
с точностью до 0,001.
Решение:
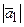 =
= 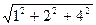 =
= 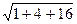 =
= 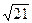 = 4,583.
= 4,583.
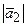 =
= 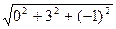 =
= 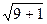 =
= 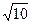 = 3,162.
= 3,162.
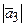 =
= 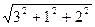 =
= 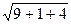 =
= 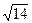 = 3,742.
= 3,742.
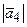 =
= 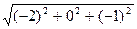 =
= 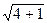 =
= 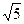 = 2,236.
= 2,236.
5. Найти значение выражения:  (2
(2  +
+  ) + 2
) + 2 
 .
.
Решение: решим по действиям
1) 2  = (0, 6, – 2).
= (0, 6, – 2).
2) (2  +
+  ) = (3, 7, 0).
) = (3, 7, 0).
3) 
 (2
(2  +
+  ) = 1
) = 1  3 + 2
3 + 2  7 +4
7 +4  0 = 3 + 14 = 17.
0 = 3 + 14 = 17.
4) 
 =
= 
 = 13.
= 13.
5) 17 + 13 = 30.
Пример 2.Даны точки в пространстве R 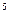 :
:
А (1, 2, 1, 3, 2), В (1, 4, 1, – 1, 0), С (1, 2, 1, 1, 1).
Найти расстояния 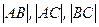 с точностью до 0,0001.
с точностью до 0,0001.
Решение:Согласно формуле
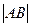 =
= 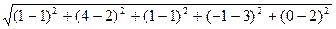 =
=
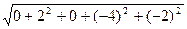 =
= 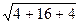 =
= 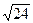 = 4,9000.
= 4,9000.
Заметим, что 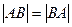 .
.
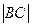 =
= 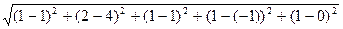 =
=
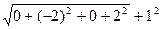 =
= 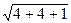
 =
= 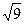 = 3,0000.
= 3,0000.
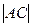 =
= 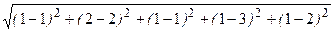 =
=
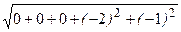 =
= 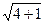 =
= 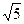 =2,2361.
=2,2361.
Пример 3. Найти вектор 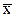 из уравнения
из уравнения
а) 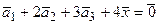 ,
,
если  = (5, – 8, – 1, 2),
= (5, – 8, – 1, 2),  = (2, – 1, 4, – 3),
= (2, – 1, 4, – 3), 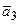 = (– 3, 2, – 5, 4).
= (– 3, 2, – 5, 4).
б) 3 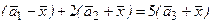 ,
,
если 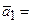 (2, 5, 1, 3),
(2, 5, 1, 3), 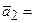 (10, 1, 5, 10),
(10, 1, 5, 10), 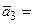 (4, 1, -1, 1).
(4, 1, -1, 1).
Решение:а)

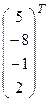 +
+ 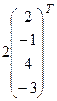 +
+ 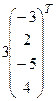 +
+ 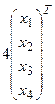 =
= 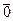 , откуда
, откуда
5 + 4 – 9 = – 4 х  0 = – х
0 = – х  х
х  = 0
= 0
– 8 – 2 + 6= – 4х  – 4 = – 4х
– 4 = – 4х  х
х  = 1
= 1
– 1 + 8 – 15= – 4х 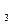 – 8 = – 4х
– 8 = – 4х 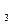 х
х 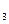 = 2
= 2
2 – 6 + 12= – 4х 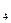 8 = – 4х
8 = – 4х 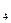 х
х 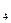 = –2
= –2
Ответ: 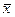 = (0, 1, 2, -2).
= (0, 1, 2, -2).
Решение:б)Преобразуем выражение (отдельно каждую скобку):
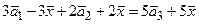
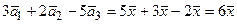
3 
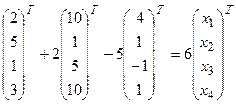
6 + 20 – 20 = 6х  6 = 6 х
6 = 6 х  х
х  = 1
= 1
15 + 2 – 5 = 6х  12 = 6 х
12 = 6 х  х
х  = 2
= 2
3 + 10 + 5 = 6х 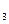 18 = 6 х
18 = 6 х 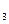 х
х 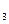 = 3
= 3
9 + 20 – 5 = 6 х 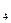 24 = 6 х
24 = 6 х 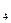 х
х 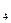 = 4
= 4
Ответ: 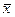 = (1, 2, 3, 4).
= (1, 2, 3, 4).
СЕМИНАР 2.
