Множества и операции над ними
ЧИСЛА.
МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ
Дано множество R действительных чисел. На нем введены операции сложения +и умножения  .
.
φ  : R
: R 
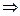
 R φ
R φ  : R
: R 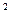
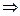
 R
R
то есть множество R замкнуто относительно операций сложения и умножения.
Свойства операций сложения и умножения чисел:
1. (a + b) + c = a + b + c для любых а, b, c 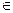 R
R
(а  b)
b)  c = a
c = a  (b
(b  c) = a
c) = a  b
b  c
c
a + b = b + a
a  b = b
b = b  a
a
a  (b + c) = a
(b + c) = a  b + a
b + a  c
c
существует единичный элемент по сложению:
обозначим его  ε
ε  = 0 , такой что для любых а
= 0 , такой что для любых а
а + 0 = 0 + а = а
для любого а существует обратный элемент по сложению,
обозначим его -а , назовем противоположным, такой что
а +(-а) = -а + а = 0
существует единичный элемент по умножению:
обозначим ε 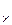 = 1 , так что для любых а
= 1 , так что для любых а
a  1 = 1
1 = 1  a = а
a = а
9. для любого а существует обратный элемент по умножению:
обозначим а 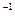 , назовем обратным, так что
, назовем обратным, так что
a  а
а 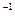 = а
= а 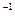
 a = 1
a = 1
Множество – это совокупность определенных различаемых объектов таких, что для любого объекта можно установить, принадлежит объект данному множеству или нет.
Далее будем рассматривать множества чисел.
Множества обычно обозначают прописными буквами, например, А. Если число принадлежит множеству, то будем говорить, что “оно является элементом множества”. Например, если а является элементом множества А, то это утверждение может быть записано следующим образом:
“ 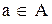 ”.
”.
Утверждение “b не является элементом А” будем обозначать
“ 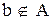 ”.
”.
Символ 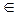 происходит от греческой буквы
происходит от греческой буквы 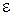 .
.
Пример:
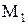 - множество всех натуральных чисел: 1, 2, 3, . . . Обозначим N. Часто 0 считают натуральным числом. Множество N с добавлением 0 обозначается
- множество всех натуральных чисел: 1, 2, 3, . . . Обозначим N. Часто 0 считают натуральным числом. Множество N с добавлением 0 обозначается 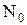 .
.
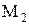 - множество всех натуральных чисел, не превосходящих 100.
- множество всех натуральных чисел, не превосходящих 100.
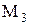 - множество всех решений уравнения
- множество всех решений уравнения 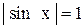 (элементы множества
(элементы множества 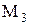 - числа, являющиеся решением).
- числа, являющиеся решением).
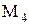 - множество всех чисел вида
- множество всех чисел вида 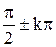 , где
, где 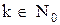 .
.
Множество А называется подмножеством множества В (обозначается 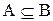 ), если всякий элемент А является элементом В.
), если всякий элемент А является элементом В.
Говорят: В содержит Аили покрывает А.
Множества А и В равны, если их элементы совпадают или если это два множества, имеющие одинаковые элементы.
Множества А и В равны, если 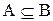 и
и 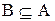 . Определение 2 указывает на наиболее типичный метод доказательства (сначала доказывается
. Определение 2 указывает на наиболее типичный метод доказательства (сначала доказывается 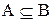 , затем обратное
, затем обратное 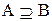 .
.
Пример:
Тригонометрическая теорема: 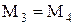 :
:
а) всякое решение уравнения 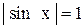 имеет вид
имеет вид 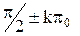
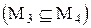 ;
;
б) всякое число вида 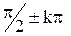 является решением уравнения sin x = 1
является решением уравнения sin x = 1 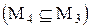 .
.
Если 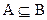 и
и 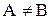 , то А называется строгим подмножеством множества В (обозначается
, то А называется строгим подмножеством множества В (обозначается 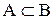 ,
, 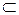 - строгое включение).
- строгое включение).
Способы задания множеств
I. Перечисление (список элементов).
II. Порождающая процедура.
III. Разрешающая процедура (описание характеристических свойств, которыми должны обладать элементы).
I. Задание множества списком
Списком можно задать лишь множества, содержащие несколько элементов. Задание типа
N = 1, 2, 3 . . .
не список, а условное обозначение, допустимое, когда оно заведомо не вызывает разногласий.
Пример:
Определим А как множество все целых чисел х строго между 6 и 10. Это можно записать следующим образом:
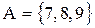
и прочитать как : “А- множество, содержащее 7, 8, 9”.
Множества часто рассматриваются как “неупорядоченные совокупности элементов”, хотя иногда полезно подчеркнуть, что, например,
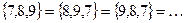 .
.
II. Порождающая процедура
Описывает способ получения элементов множества из уже полученных элементов либо других объектов. Тогда элементы множества - все объекты, которые могут быть получены (построены) с помощью такой процедуры.
Примеры:1) Описание множества 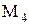 (множество всех чисел вида
(множество всех чисел вида 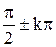 ), где исходные объекты для построения множества - натуральные числа, а порождающая процедура для вычисления описана формулой
), где исходные объекты для построения множества - натуральные числа, а порождающая процедура для вычисления описана формулой 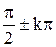 .
.
2) Множество 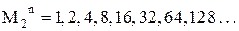
Порождающая процедура определяется двумя правилами:
а) 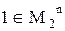 ; б) если
; б) если 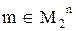 , то
, то 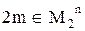 .
.
Правила, описанные таким образом, называются индуктивными или рекурсивными.
III. Задание множества описанием его элементов (разрешающая процедура)
Примеры:
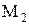 - множество всех натуральных чисел (N).
- множество всех натуральных чисел (N).
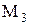 - множество всех решений уравнения
- множество всех решений уравнения 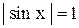 .
.
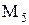 - множество всех действительных чисел.
- множество всех действительных чисел.
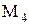 - множество всех чисел
- множество всех чисел 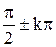 , где
, где 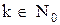 можно интерпретировать как описание свойства его элементов, заключающегося в возможности представить их в виде
можно интерпретировать как описание свойства его элементов, заключающегося в возможности представить их в виде 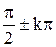 .
.
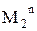 - заданное как “множество всех целых чисел, являющихся степенью двойки”,
- заданное как “множество всех целых чисел, являющихся степенью двойки”, 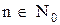 . Такой способ задания множества применяется, когда свойство элементов М может быть описано коротким выражением. Например, P(x) читается: «х обладает свойством Р», то М задается при помощи обозначения
. Такой способ задания множества применяется, когда свойство элементов М может быть описано коротким выражением. Например, P(x) читается: «х обладает свойством Р», то М задается при помощи обозначения 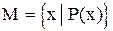 читается: «М - множество элементов х, обладающих свойством Р».
читается: «М - множество элементов х, обладающих свойством Р».
Примеры:
1) 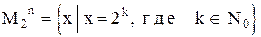 .
.
2) 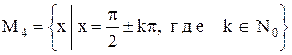 .
.
Требования к описанию свойств - точность и недвусмысленность.
Надежный способ точно описать свойства элементов данного множества - задание распознающей (разрешающей) процедуры, которая для любого объекта устанавливает, обладает он свойством или нет (т. е. является элементом множества или нет).
Пример:Для 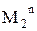 , то есть для свойства, быть степенью двойки разрешающей процедурой является любой метод разложения целых чисел на простые множители. Здесь разрешающая процедура не является порождающей. Но ее нетрудно таковой сделать: например, порождающая процедура может быть таковой. Берем последовательно все натуральные числа и каждые из них разлагаем на простые множители: те числа, которые не содержат множителей, отличных от двойки, включаем в
, то есть для свойства, быть степенью двойки разрешающей процедурой является любой метод разложения целых чисел на простые множители. Здесь разрешающая процедура не является порождающей. Но ее нетрудно таковой сделать: например, порождающая процедура может быть таковой. Берем последовательно все натуральные числа и каждые из них разлагаем на простые множители: те числа, которые не содержат множителей, отличных от двойки, включаем в 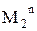 .
.
Пустое множество (обозначается 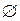 ) есть множество, обладающее свойством:
) есть множество, обладающее свойством:
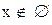 при любом х.
при любом х.
Другое множество, определение которого зависит от задачи, называют универсальным множеством.
Универсальное множество (обозначается U) есть множество всех рассматриваемых в данной задаче элементов.
Рассмотрим теперь множество 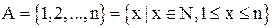 . Оно имеет n элементов. Будем говорить, что мощность этого множества есть n.
. Оно имеет n элементов. Будем говорить, что мощность этого множества есть n.
Мощностью (длиной, размерностью) множества называется число элементов этого множества. Обозначим 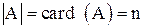 .
.
Далее любое множество В, которое имеет то же число элементов, что и А, имеет такую же мощность, и естественно, эти элементы не надо пересчитывать. Для небольших множеств достаточно легко пересчитать элементы, но для других множеств, например N, это может быть невозможно. Далее следует строгое, но неформальное определение количества элементов.
Говорят, что множество Х конечно, если 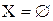 или для некоторого
или для некоторого 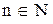 существует множество
существует множество 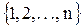 такое, что оно имеет то же самое число элементов, что и X. Если
такое, что оно имеет то же самое число элементов, что и X. Если 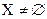 и никакого n не может быть найдено, то Х называют бесконечным.
и никакого n не может быть найдено, то Х называют бесконечным.
Операции над множествами
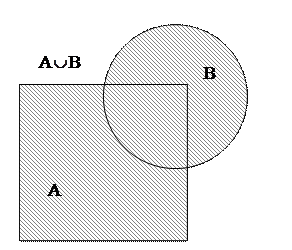
Объединением множеств АиВ (обозначается 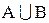 ) называется множество, состоящее из всех тех элементов, которые принадлежат или А, или В или А и В одновременно, т. е. хотя бы одному из множеств А и В.
) называется множество, состоящее из всех тех элементов, которые принадлежат или А, или В или А и В одновременно, т. е. хотя бы одному из множеств А и В.
Символическая запись
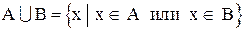 .
.
 Определение объединения произвольного числа множеств аналогично.
Определение объединения произвольного числа множеств аналогично.
Запись:
а)  и т. д. используется если совокупность содержит небольшое число множеств;
и т. д. используется если совокупность содержит небольшое число множеств;
б)  означает: объединение всех множеств А, принадлежащих совокупности S;
означает: объединение всех множеств А, принадлежащих совокупности S;
в) 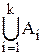 используется для случаев, когда
используется для случаев, когда 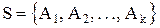 ;
;
г) 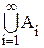 используется для случаев, когда
используется для случаев, когда 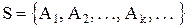 – бесконечная совокупность и ее множества занумерованы подряд натуральными числами;
– бесконечная совокупность и ее множества занумерованы подряд натуральными числами;
д) 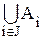 - для случаев, когда набор индексов множества задан множеством J.
- для случаев, когда набор индексов множества задан множеством J.
Пример:
1) 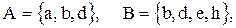 тогда
тогда 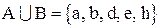 .
.
Пересечениеммножеств А и В (обозначается 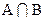 ) называется множество, состоящее из всех тех и только них элементов, которые принадлежат А и В одновременно.
) называется множество, состоящее из всех тех и только них элементов, которые принадлежат А и В одновременно.
Символическая запись 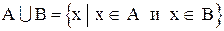 .
.
 Пересечение произвольной совокупности множеств (в том числе и бесконечной) - определяется аналогично.
Пересечение произвольной совокупности множеств (в том числе и бесконечной) - определяется аналогично.
Пример:
1) 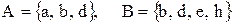 , тогда
, тогда 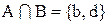 .
.
Как следствие этих определений мы имеем
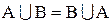 ,
, 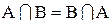 ,
,
и, что менее очевидно,
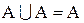 ,
, 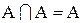 .
.
Разбиением множества U называется система множеств 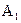 ,
, 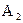 ,…,
,…, 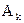 , … в которой все попарные пересечения пусты, а их объединение совпадает U, т. е.
, … в которой все попарные пересечения пусты, а их объединение совпадает U, т. е.
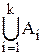 = U,
= U, 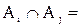
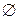 .
.
Класс разбиения (блок разбиения) есть множество такой системы множеств.
Покрытием множества А называется система множеств 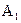 ,
, 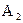 ,…,
,…, 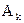 , …, возможно пересекающихся, объединение которых содержит все элементы множества А, т.е.
, …, возможно пересекающихся, объединение которых содержит все элементы множества А, т.е.
U 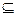
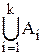
Разностью множеств А и В 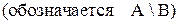 называется множество всех тех и только тех элементов А, которые не принадлежат В:
называется множество всех тех и только тех элементов А, которые не принадлежат В:
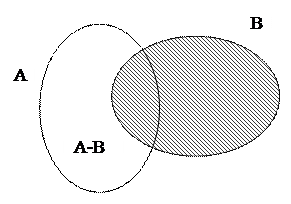
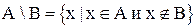 .
.
Разность - операция строго двухместная (т. е. определена для двух множеств) и некоммутативная.
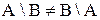 .
.
Если 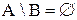 , то
, то 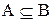 .
.
Пример:
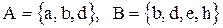 , тогда
, тогда 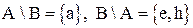 .
.
Дополнением (до U) множества А 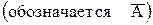 называется множество всех элементов, не принадлежащих А (но принадлежащих U):
называется множество всех элементов, не принадлежащих А (но принадлежащих U):
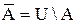 .
.
Множество U должно быть задано либо очевидно.
Пример:
Из определения 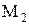 очевидно, что
очевидно, что 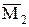 - множество всех натуральных чисел, больших 100.
- множество всех натуральных чисел, больших 100.
Свойства операций над множествами:
1) 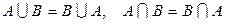 ;
;
2) 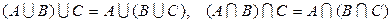 ;
;
3) 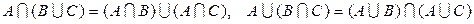 ;
;
4) 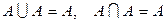 ;
;
5) 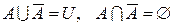 ;
;
6) 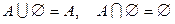 ;
;
7) 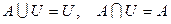 ;
;
8) 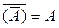 ;
;
9) 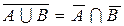 ,
, 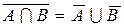 .
.
Прямым (декартовым) произведением двух множеств А и В ( 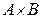 ) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
) называется множество, состоящее из упорядоченных пар элементов, в которых первый элемент принадлежит множеству А, а второй – множеству В.
Пример: 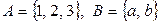 ,тогда
,тогда 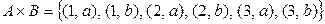 .
.
Если в прямое произведение вступают несколько одинаковых множеств, то это можно обозначить 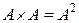 ,
, 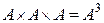 и т. д.
и т. д.
Пример:Множество 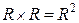 это множество точек декартовой плоскости.
это множество точек декартовой плоскости.
СЕМИНАР 1.
Вопросы
1. Что такое множество.
2. Как задаются множества
3. Что такое пустое множество
4. Что такое универсальное множество.
5. Как определяется мощность множества.
6. Какое множество называется счетным.
7. Какое множество называется континуальным.
8. Как определяется объединение множеств.
9. Как определяется пересечение множеств.
10. Что такое разность множеств.
11. Из каких элементов состоит множество  .
.
Задачи
1. Укажите смысловые связки естественного языка, соответствующие основным операциям над множествами: дополнение (– НЕ), объединение (сумма) (– ИЛИ), пересечение (произведение) (– И), разность (– БЕЗ).
2. Пусть 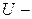 множество сотрудников некоторого предприятия;
множество сотрудников некоторого предприятия; 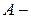 множество всех сотрудников старше 40 лет;
множество всех сотрудников старше 40 лет; 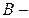 множество сотрудников, имеющих стаж более 10 лет;
множество сотрудников, имеющих стаж более 10 лет; 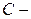 множество служащих;
множество служащих; 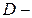 множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества.
множество рабочих. Каков содержательный смысл каждого из нижеследующих множеств? Изобразить графически (с помощью диаграмм Эйлера – Венна) эти множества.
а) 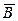 ; ; | д) 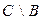 ; ; | и) 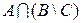 ; ; |
б) 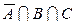 ; ; | е) 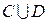 ; ; | к) 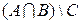 |
в) 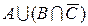 ; ; | ж) 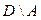 ; ; | л) 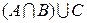 ; ; |
г) 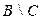 ; ; | з) 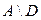 | м) 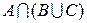 . . |
3. Заданы два множества: А = {1, 5, 7, 9, 12} и B = {5, 7, 9, 11, 13}. Найти множества 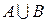 ;
; 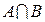 ;
; 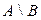 ;
; 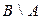 и их мощность.
и их мощность.
4. По заданным промежуткам А и B на числовой оси определить 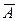 ;
; 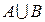 ;
; 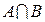 ;
; 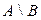 ;
; 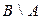 .
.
а) 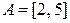 и
и 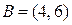 ; б)
; б) 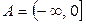 и
и 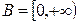 ;
;
в) 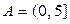 и
и 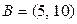 ; г)
; г) 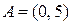 и
и 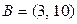
5. Построить из множества А, В и С результат операций над ними. А={1, 2, 3}, В={1, 3, 5}, С={2, 3, 4, 6}.
а) 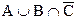 ; б)
; б) 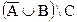 .
.
6. Пусть Множества А, В, С пересекаются в наиболее общем случае. Изобразить на диаграмме Эйлера Результат следующих действий:
а) 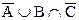 ; б)
; б) 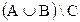 ; в)
; в) 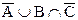 ; г)
; г) 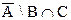 . 7. Пусть А и В – произвольные подмножества универсального множества U Доказать графически, что:
. 7. Пусть А и В – произвольные подмножества универсального множества U Доказать графически, что:
а) 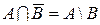 ; в)
; в) 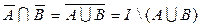 ;
;
б) 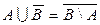 ; г)
; г) 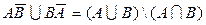 ;
;
д) 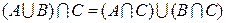 .
.
8. Пусть 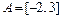 и
и 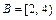 - промежутки на числовой оси. Найти
- промежутки на числовой оси. Найти 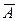 ;
; 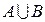 ;
; 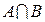 ;
; 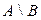 ;
; 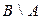 .
.
9.Определить мощности множеств 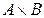 ;
; 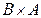 ;
; 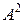 ;
; 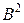 ;
; 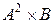 ;
; 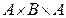 , и построить их, если
, и построить их, если
а) 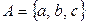 ;
; 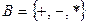 ; б)
; б) 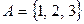 ;
; 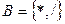 ;
;
в) 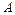 = {(1; 2)},
= {(1; 2)}, 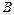 = {a; b; c; d}; г)
= {a; b; c; d}; г) 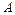 = {1; 2; 3},
= {1; 2; 3}, 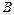 = {1; 2}.
= {1; 2}.
10. Пусть 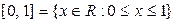 ;
; 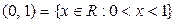 ;
; 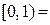
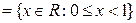 и
и 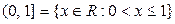 . Описать и изобразить графически следующие множества
. Описать и изобразить графически следующие множества
а) 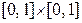 ; б)
; б) 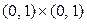 ; в)
; в) 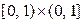 ; г)
; г) 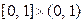 .
.
ВЕКТОРЫ. ОПЕРАЦИИ НАД НИМИ
Элементы пространства R 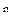 называются n-мерными векторами. Обозначаем:
называются n-мерными векторами. Обозначаем:  =(х
=(х  ,х
,х  ,…х
,…х 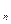 ), где
), где  (i=
(i= 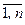 ) называются координаторами вектора
) называются координаторами вектора  , n – размерность вектора
, n – размерность вектора  .
.
Размерность можно обозначить так dim  = n.
= n.
Чтобы умножить вектор  = (х
= (х  , х
, х 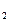 ,…х
,…х 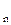 )на скаляр k, надо каждую координату вектора
)на скаляр k, надо каждую координату вектора  умножить на скаляр k.
умножить на скаляр k.
k 
 = (k
= (k  х
х  , k
, k  х
х 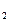 ,… k
,… k  х
х 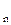 ).
).
Чтобы сложить два n-мерных вектора  =(х
=(х  , х
, х 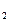 ,…х
,…х 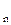 ) и
) и  = (у
= (у  ,у
,у  ,…,у
,…,у 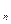 ), надо сложить соответствующие координаты.
), надо сложить соответствующие координаты.
 +
+  = (х
= (х  + у
+ у  , х
, х 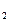 + у
+ у  , … х
, … х 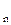 + у
+ у 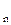 ).
).
Скалярным произведением векторов  и
и  называется число, находимое по формуле:
называется число, находимое по формуле:

 = х
= х  у
у  + х
+ х 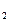 у
у  + … +х
+ … +х 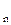 у
у 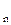 =
= 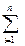 х
х 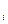 у
у 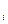 .
.
Примеры решения задач
Пример 1. Дана система векторов в R 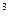 :
:
 = (1, 2, 4);
= (1, 2, 4);  = (0, 3, – 1);
= (0, 3, – 1);  = (3, 1, 2);
= (3, 1, 2); 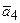 = (– 2, 0, – 1).
= (– 2, 0, – 1).
1. Найти линейные комбинации этих векторов.
а) 2  –
–  +
+  –
– 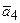 ; б)
; б)  + 2
+ 2  – 3
– 3  +
+ 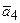 ; в) –
; в) –  –
–  –
–  –
– 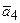 .
.
Решение:
а) 2 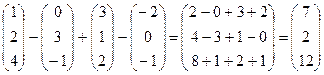 .
.
б) 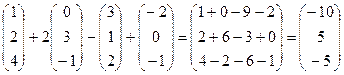 .
.
в) – 
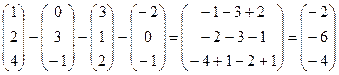 .
.
2. Найти значение выражения: 2(  +
+  ) – 3(
) – 3(  – 4
– 4  ).
).
Решение:
2(  +
+  ) – 3(
) – 3(  – 4
– 4  ) = 2
) = 2  + 2
+ 2  – 3
– 3  + 12
+ 12  = 2
= 2  –
–  + 12
+ 12  =
=
=2 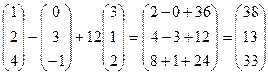 .
.
3. Найти скалярные произведения:

 ,
, 
 ,
, 
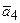 ,
, 
 ,
, 
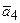 ,
, 
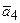 .
.
Решение:

 = 1
= 1  0 + 2
0 + 2  3 + 4
3 + 4  (–1) = 6 –4 = 2;
(–1) = 6 –4 = 2;

 = 1
= 1  3+2
3+2 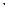 1+4
1+4  2 = 3 + 2 + 8 = 13;
2 = 3 + 2 + 8 = 13;

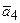 = 1
= 1  (–2) + 2
(–2) + 2  0 + 4
0 + 4  (–1) = –2 –4 = –6;
(–1) = –2 –4 = –6;

 = 0
= 0  3 + 3 1+ (–1)
3 + 3 1+ (–1)  2 = 3 –2 = 1;
2 = 3 –2 = 1;

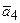 = 3
= 3  (–2) + 3
(–2) + 3  0 +(–1)
0 +(–1)  ( –1) = 1 ;
( –1) = 1 ;

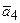 = 3
= 3  (–2) + 1
(–2) + 1  0 + 2
0 + 2  (–1) = –6 –2 = –8.
(–1) = –6 –2 = –8.
4. Найти длины векторов 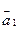 ,
, 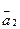 ,
, 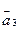 ,
, 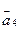 с точностью до 0,001.
с точностью до 0,001.
Решение:
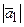 =
= 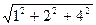 =
= 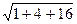 =
= 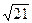 = 4,583.
= 4,583.
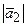 =
= 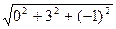 =
= 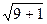 =
= 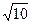 = 3,162.
= 3,162.
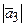 =
= 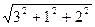 =
= 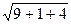 =
= 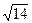 = 3,742.
= 3,742.
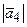 =
= 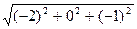 =
= 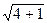 =
= 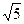 = 2,236.
= 2,236.
5. Найти значение выражения:  (2
(2  +
+  ) + 2
) + 2 
 .
.
Решение: решим по действиям
1) 2  = (0, 6, – 2).
= (0, 6, – 2).
2) (2  +
+  ) = (3, 7, 0).
) = (3, 7, 0).
3) 
 (2
(2  +
+  ) = 1
) = 1  3 + 2
3 + 2  7 +4
7 +4  0 = 3 + 14 = 17.
0 = 3 + 14 = 17.
4) 
 =
= 
 = 13.
= 13.
5) 17 + 13 = 30.
Пример 2.Даны точки в пространстве R 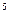 :
:
А (1, 2, 1, 3, 2), В (1, 4, 1, – 1, 0), С (1, 2, 1, 1, 1).
Найти расстояния 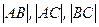 с точностью до 0,0001.
с точностью до 0,0001.
Решение:Согласно формуле
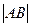 =
= 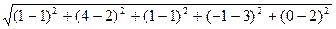 =
=
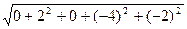 =
= 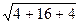 =
= 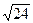 = 4,9000.
= 4,9000.
Заметим, что 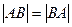 .
.
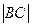 =
= 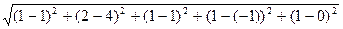 =
=
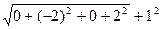 =
= 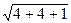
 =
= 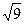 = 3,0000.
= 3,0000.
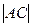 =
= 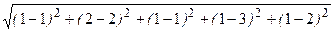 =
=
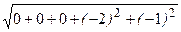 =
= 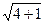 =
= 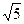 =2,2361.
=2,2361.
Пример 3. Найти вектор 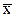 из уравнения
из уравнения
а) 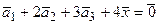 ,
,
если  = (5, – 8, – 1, 2),
= (5, – 8, – 1, 2),  = (2, – 1, 4, – 3),
= (2, – 1, 4, – 3), 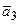 = (– 3, 2, – 5, 4).
= (– 3, 2, – 5, 4).
б) 3 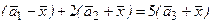 ,
,
если 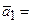 (2, 5, 1, 3),
(2, 5, 1, 3), 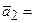 (10, 1, 5, 10),
(10, 1, 5, 10), 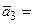 (4, 1, -1, 1).
(4, 1, -1, 1).
Решение:а)

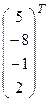 +
+ 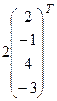 +
+ 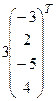 +
+ 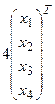 =
= 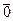 , откуда
, откуда
5 + 4 – 9 = – 4 х  0 = – х
0 = – х  х
х  = 0
= 0
– 8 – 2 + 6= – 4х  – 4 = – 4х
– 4 = – 4х  х
х  = 1
= 1
– 1 + 8 – 15= – 4х 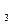 – 8 = – 4х
– 8 = – 4х 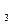 х
х 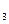 = 2
= 2
2 – 6 + 12= – 4х 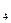 8 = – 4х
8 = – 4х 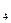 х
х 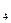 = –2
= –2
Ответ: 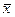 = (0, 1, 2, -2).
= (0, 1, 2, -2).
Решение:б)Преобразуем выражение (отдельно каждую скобку):
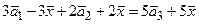
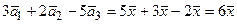
3 
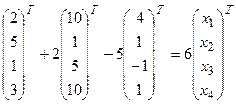
6 + 20 – 20 = 6х  6 = 6 х
6 = 6 х  х
х  = 1
= 1
15 + 2 – 5 = 6х  12 = 6 х
12 = 6 х  х
х  = 2
= 2
3 + 10 + 5 = 6х  18 = 6 х
18 = 6 х 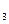 х
х 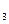 = 3
= 3
9 + 20 – 5 = 6 х 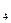 24 = 6 х
24 = 6 х 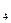 х
х 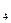 = 4
= 4
Ответ: 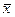 = (1, 2, 3, 4).
= (1, 2, 3, 4).
СЕМИНАР 2.
Вопросы
1. Закон коммутативности сложения.
2. Закон коммутативности умножения.
3. Закон ассоциативности сложения.
4. Закон ассоциативности умножения.
5. Закон дистрибутивности.
6. Определение n-мерного вектора, его координат.
7. Размерность вектора.
8. Когд
