Некоторые свойства длин отрезков

1. При выбранной единице длины длина любого отрезка выра­жается положительным действительным числом и для каждого по­ложительного действительного числа есть отрезок, длина которого выражается этим числом.

2. Если два отрезка равны, то равны численные значения их длин, и обратно: если равны численные значения длин отрезков, то равны и сами отрезки (при одной и той же единице длины).

3. При замене единицы длины численное значение длины уве­личивается (уменьшается) во столько раз, во сколько раз новая еди­ница меньше (больше) старой.

Примеры заданий для младших школьников, в которых раскры­ваются эти свойства:

1) — Измерь длину данного отрезка в сантиметрах.

— Какова его длина? (5 см)

— Начерти отрезок на 1 см длиннее.

— Какова длина второго отрезка? (6 см)

2)— Найди две одинаковые по длине полоски. Проверь наложе­нием.

— Измерь длину синей полоски в дециметрах. (3 дм)

— Чему равна длина красной полоски? (3 дм)

— Надо ли ее измерять? Почему?

3)— Измерь отрезок в дециметрах. (2 дм)

— Какова длина этого отрезка в сантиметрах? (20 см)

— Почему? (1 дм-10 см)

Кроме специальных упражнений учащимся начальной школы предлагаются задачи, в которых используются понятия длины, ее измерения, требуется перевод единиц. Школьников учат построе­нию вспомогательных моделей при решении задач, используя отрез­ки разной длины и пр.

Задание 52

Решите задачи, используя вспомогательные модели:

1. Вдоль прямой дороги растут 5 деревьев. Расстояние между со­седними деревьями 2 метра. Каково расстояние между крайними деревьями?

2. У Пеги было 2 карандаша, у Коли 4 карандаша, а у Миши столь­ко, сколько у Пети и Ноли вместе. Сколько всего было каранда­шей у мальчиков?

Площадь фигуры

Понятие о площади фигуры имеет любой человек, при этом из­вестны и свойства этой величины: площадь квартиры слагается из площадей всех ее повещений, одинаковые земельные участки име­ют одинаковую площадь.

Площадь — положительная величина, определенная на множес­тве плоских фигур так, что:

-равные фигуры имеют равные площади;

-если фигура составлена из конечного числа фигур, то ее площадь равна сумме их площадей.

Процесс измерения площади (рис. 83):

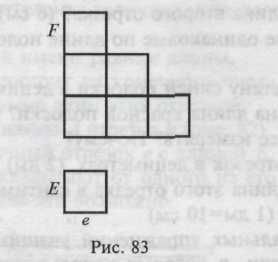1) Выбирают единицу площади Е (обычно квадрат со стороной, равной единичному отрезку ё).

2) Сравнивают площадь фигуры с площадью единичного квад­рата Е.

3) Результат сравнения обозначают числом и называют числен­ным значением площади.

SF = х-Е, где х — численное значение площади.

Дошкольники могут встретиться с понятием площади и ее изме­рения, например, в такой игре, как «Пентамино» (рис. 84): «Пред­ставь, что это плоты. На одной клеточке помешается один человек. Какой плот может перевезти больше людей? Почему?

Для нахождения численного значения площади фигур часто пользуются не измерением, а вычислением, что удобно, но для это­го нужно знать формулы.

Задание 55

Сформулируйте определение объеме тепа, процессе его измере­ния и свойства (по аналогии с площадью).

В начальной школе в процессе изучения геометрического мате­риала у детей появляется представление о площади как о свойстве плоских геометрических фигур. Опыт сравнения площадей фигур «на глаз» и наложением, полученный в детском саду, получает свое применение при ознакомлении со свойствами площадей. С объемом жидких и сыпучих веществ знакомят уже дошкольников. В процессе переливания, пересыпания дети знакомятся с объемом, измеряя его условными мерками (ложками, стаканами и др.).

Задание 56

Придумайте задание для дошкольника, в процессе которого он будет измерять объем коробки.

Масса тела

Понятие о массе тела или вещества возникло из необходимости человека обменивать и продавать товары, продукты. Для измерения массы были придуманы рычажные весы и гири.

Масса— одна из основных физических величин, которая свя­зана с весом (силой, с которой тело давит на опору или оттягивает подвес в результате притяжения Земли). На различных широтах (на­пример, на полюсе и на экваторе) вес одного и того же тела отлича­ется. Масса же остается неизменной и является характеристикой только данного тела.

С математической точки зрения:

Масса- это положительная величина, определенная на мно­жестве физических тел так, что:

— масса одинакова у тел, уравновешивающих друг друга на весах;

— массы складываются, когда тела соединяются вместе.

Замечание.

Весы получили свое название вследствие того, что на них измеря­ют вес предмета. Вес как сила измеряется в ньютонах и связан с мас­сой формулой F=mg, в статичном положении отличается от нее только коэффициентом 9,8 (ускорение свободного падения), что позво­ляет шкалу на весах сразу обозначить в килограммах, а не в ньютонах.

Масса характеризуется теми же свойствами, что длина и пло­щадь, только на множестве физических тел. Сравнение масс, дей­ствия над ними сводятся к сравнению и действиям над численными значениями масс.

Процесс измерения массы

1. Выбирают тело, масса которого принимается за единицу (предполагается, что можно взять и ее доли 0,1; 0,01 и т.д.).

2. На одну чашу весов кладут измеряемое тело, а на другую - тела, выбранные в качестве единицы массы (гири) так, чтобы весы были уравновешены.

3.Считают численное значение массы гирь. Это и будет числен­ным значением искомой массы.

При развитии барического чувства («чувства тяжести»), при зна­комстве со способами определения массы на весах, дети уже дош­кольного возраста сталкиваются со свойствами массы, сравнением предметов по массе, действиями с численными значениями масс. Происходит это, например, при рассматривании рисунков или ре­альных предметов.

Рисунок 1: на левой чаше весов — 1 яблоко, на правой чаше ве­сов — 8 желудей, весы уравновешены.

Рисунок 2: на левой чаше весов — 1 груша, на правой чаше ве­сов - 6 желудей, весы уравновешены.

Вопрос: «Что тяжелее — яблоко или груша?»

Младших школьников знакомят с общепринятыми единицами массы: килограммом, граммом. Понятие массы используется в зада­чах.

Более подробно понятие массы изучается школьниками на уро­ках физики. В процессе математического развития дошкольников и на уроках математики в начальной школе происходит первоначаль­ное знакомство детей с массой в целях сенсорного воспитания и ис­пользования при решении арифметических задач.

Задание 57

Решите задачу: «Имеются рычажные весы и 3 гири 8 кг, 5 кг, 3 кг. Как одним взвешиванием отмерить 6 кг крупы?»

Промежутки времени

Окружающий нас мир существует во времени. Временные ха­рактеристики явлений (продолжительность, последовательность, частота, ритм, темп и др.) необходимы для описания любых процес­сов в природе. Понятие времени более сложное, чем понятие длины, площади, массы. Оно не имеет наглядности и познается опосредо­ванно. Вся жизнь человека связана со временем, с умением изме­рять, распределять, ценить время. Время течет непрерывно, его нельзя ни остановить, ни возвратить, ни увидеть, что создает осо­бые трудности в изучении.

В математике и физике время рассматривают как скалярную ве­личину, ее свойства похожи на рассмотренные ранее.