Взаимосвязь величин и их численных значений

1. Если величины А а В измерены с помощью единицы величи­ны Е, то отношения между величинами А к В будут такими же, как и отношения между их численными значениями (и наоборот):

— объем аквариума 3 м3, выразите его в литрах (л);

— площадь земельного участка 80 000 м2, выразите ее в гектарах (га).

Дошкольники знакомятся с измерением величин сначала с по­мощью условных мерок. В процессе практической деятельности они осознают взаимосвязь величины и ее численного значения, а также численного значения величины от выбранной единицы измерения.

Примеры.

1. Измерь шагами длину дорожки от дома до дерева, а теперь от дерева до забора. Какова длина всей дорожки? (Дети складывают величины, пользуясь их численными значениями.)

2. Какова длина дорожки, измеренная шагами Маши? (5 шагов.)

— Какова длина этой же дорожки, измеренная шагами Коли? (4 шага.)

— Почему мы измеряли длину одной и той же дорожки, а по­лучили разные результаты? (Длина дорожки измерена раз­ными шагами. Шаги Коли длиннее, поэтому их получилось меньше.)

Вывод: численные значения длины дороги отличаются из-за применения разных единиц измерения.

Потребность в измерении величин возникла в практической де­ятельности человека в процессе его развития. Результат измерения выражается числом и дает возможность глубже осознать суть поня­тия числа. Сам процесс измерения учит детей логически мыслить, формирует практические навыки, обогащает познавательную дея­тельность. В процессе измерения дети могут получить не только на­туральные числа, но и действительные. Это создает мотивацию для изучения дробей.

При решении задач с использованием величин очень важно на­учить детей вычленять такие понятия:

— объект (предмет, явление, процесс),

— величину,

— численное значение величины,

— единицу величины.

Задание 51

Выявите объекты, величины, их численные значения и единицы, в которых они измерены, в приведенных предложениях:

— «Мама купила 5 кг яблок, 3 л молока и 6 лл ткани»;

— «На приготовление уроков Оля истратила 2 ч»;

— «Лекарство полностью растворяется в воде за 30 с».

Длина отрезка

Первые представления о длине как свойстве предметов возника­ют у детей довольно рано. Познавая трехмерность пространства, дошкольники учатся выделять в предмете длину, ширину, высоту, обозначать словами их отношения и даже измерять величины услов­ными мерками. Все эти термины отражают одно и то же свойство предметов «иметь протяженность».

Длина - это положительная величина, определенная на множес­тве отрезков так, что:

— равные отрезки имеют равные длины,

— если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.

Процесс измерения длины Л отрезка а (рис. 82)

1. Выбирают единичный отрезок е с длиной Е.

2. На отрезке а откладывают от одного из его концов отрезки, равные единичному, пока это возможно.

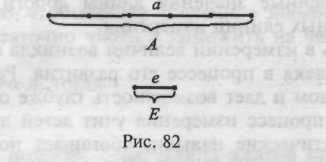
3. Подсчитывают количество отложенных отрезков:

— если отрезок отложили л раз и конец последнего совпал с концом отрезка а, то численное значение длины отрезка а есть натуральное число n, а его длина А-nЕ,

— если отрезок е отложили n раз и получился остаток, меньший е, то на нем откладывают отрезки, равные е,=0,1е, е3=0,01е и тд. Таким образом, численное значение длины отрезка а бу­дет выражено десятичной дробью, то есть положительным действительным числом х, и длина отрезка А—хЕ.