Понятие множества и элемента множества

В конце XIX века возникла новая область математики — теория множеств, одним из создателей которой был немецкий математик Георг Кантор (1845 — 1918). Эта теория, несмотря на небольшой возраст, стала фундаментом всей математики.

Множество — одно из основных математических понятий, поэ­тому не имеет явного определения, а поясняется на примерах. Оно возникло как обобщение таких понятий, как класс, группа, сово­купность, набор, стая, стадо и др.

Можно говорить о множестве домов на улице, о множестве пальцев на руке у человека, множестве углов у квадрата, множестве натуральных чисел.

Элементы множества — объекты, из которых образовано мно­жество.

Различают множества конечные и бесконечные. Например, мно­жество страниц в книге - это конечное множество, а множество то­чек на прямой — бесконечное множество.

В русском языке слово «множество» обозначает большое число предметов. В математике рассматривают не только множества с большим числом элементов, но и одноэлементные множества, а также пустое множество, которое не содержит ни одного элемента.

На рисунке 26 можно увидеть примеры различных множеств.

Множества обозначают заглавными буквами латинского алфавита: А, В, С. Для некоторых числовых множеств приняты стандартные обозначения:

N - множество натуральных чисел;

Z — множество целых чисел;

Q — множество рациональных чисел;

/ - множество иррациональных чисел;

R - множество действительных чисел.

Ø — символ, обозначающий пустое множество.

2.2. Способы задания множеств

Так как понятие множества не имеет явного определения, необходимо научиться узнавать, является ли данная совокупность множеством или нет. Считают, что множество определяется своими элементами.

Множество задано, если о любом объекте можно сказать, принад­лежит он этому множеству либо не принадлежит.

Способы задания множеств:

• перечислить все его элементы (применяется для задания мно­жеств с небольшим количеством элементов, иногда для бес­конечных, если понятно, какие элементы не указываются):

Названные способы задания множеств взаимосвязаны — если конечное множество задано с помощью характеристического свой­ства, то можно его элементы перечислить, и наоборот.

Задание 19.

Отношения между множествами

Два множества могут пересекаться и не пересекаться.

Задание 20

Назовите множества, которые можно выделить на рисунке 30. По­кажите их элементы. Сколько элементов в каждом множестве?

Берлине). Множества, независимо от количества элементов в них, изображают при помощи кругов (рис. 31).

Итак, можно выделить разные отношения между множествами:

1) множества не пересекаются;

2) множества пересекаются:

— множества имеют общие элементы, но ни одно не является подмножеством другого;

— одно множество является подмножеством другого, но мно­жества неравны;

— множества равны.

Задание 22

1. Изобразите при помощи кругов Эйлера отношения между мно­жествами, выделенными вами на рисунке 30.

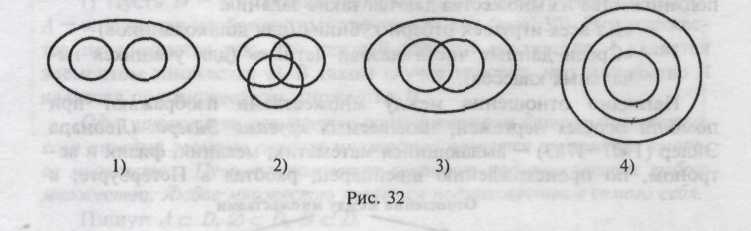
2. Установите, какой из чертежей на рисунке 32 отражает отноше­ний между следующими множествами:

а) множество натуральных чисел, множество целых чисел, множе­ство рациональных чисел;

б) объем понятия я четырех угольник», объем понятия «прямоуголь­ник», объем понятия «ромб»;

в) множество пальцев на правой руке, множество пальцев на левой ноге, множество пальцев у человека;

г) объем понятия «женское имя», объем понятия «мужское имя», объем понятия «кличка животного».

Операции над множествами

Из элементов двух множеств можно образовывать новые мно­жества, которые являются результатом определенных операций над множествами.

Задание 23

Начертите два треугольника так, чтобы их пересечением были:

— точка;

— отрезок;

— треугольник;

— четырехугольник;

— пятиугольник;

— шестиугольник.

Задан

Задание 24

Задание 26

1. Перечислите элементы дополнения множества летних месяцев до множестве месяцев года.

2. Назовите характеристическое свойство дополнения множества А до N — множества натуральных чисел, если:

А — множество четных натуральных чисел; А - множество чисел, кратных 5; А - множество чисел, больших 10.