Математическое доказательство

Приведем пример использования неполной индукции в работе с дошкольниками: используя игру «Чудесный мешочек» с объемными геометрическими фигурами, лаем задание ребенку: «Достань фигуру и назови». После нескольких попыток ребенок делает предположе­ние:

- Шар. Шар. Шар. Здесь, наверное, все шары.

Задание 14

Предложите дальнейшие рассуждения для того, чтобы убедиться в истинности (или ложности) полученного утверждения.

Невозможно переоценить значение доказательств в нашей жиз­ни и особенно в науке. К доказательствам прибегают все, но не всегда задумываются, что значит «доказать*. Практические навыки доказательства и интуитивные представления о нем достаточны для многих бытовых целей, но не для научных.

Доказать какое-либо утверждение — это показать, что это логи­ческое утверждение логически следует из системы истинных и связан­ных с ним утверждений.

Доказательство является логической операцией обоснования ис­тинности какого-либо утверждения с помощью других истинных и связанных с ним утверждений.

В доказательстве выделяют три структурных элемента:

1) доказываемое утверждение;

2) систему истинных утверждений, с помощью которых обосно­вывается истинность доказываемого;

3) логическую связь между пп. 1 и 2.

Основным способом математического доказательства является дедуктивный вывод.

По своей форме доказательство— это дедуктивное умозаключе­ние или цепочка дедуктивных умозаключений, ведущих от истин­ных посылок к доказываемому утверждению.

В математическом доказательстве важен порядок расположения умозаключений. По способу ведения различают прямые и косвенные доказательства. К прямым доказательствам относится полная индук­ция, речь о которой шла в п.1.6.

Полная индукция - способ доказательства, при котором истин­ность утверждения следует из его истинности во всех частных слу­чаях.

Полная индукция часто применяется в играх с дошкольниками типа: «Назови одним словом».

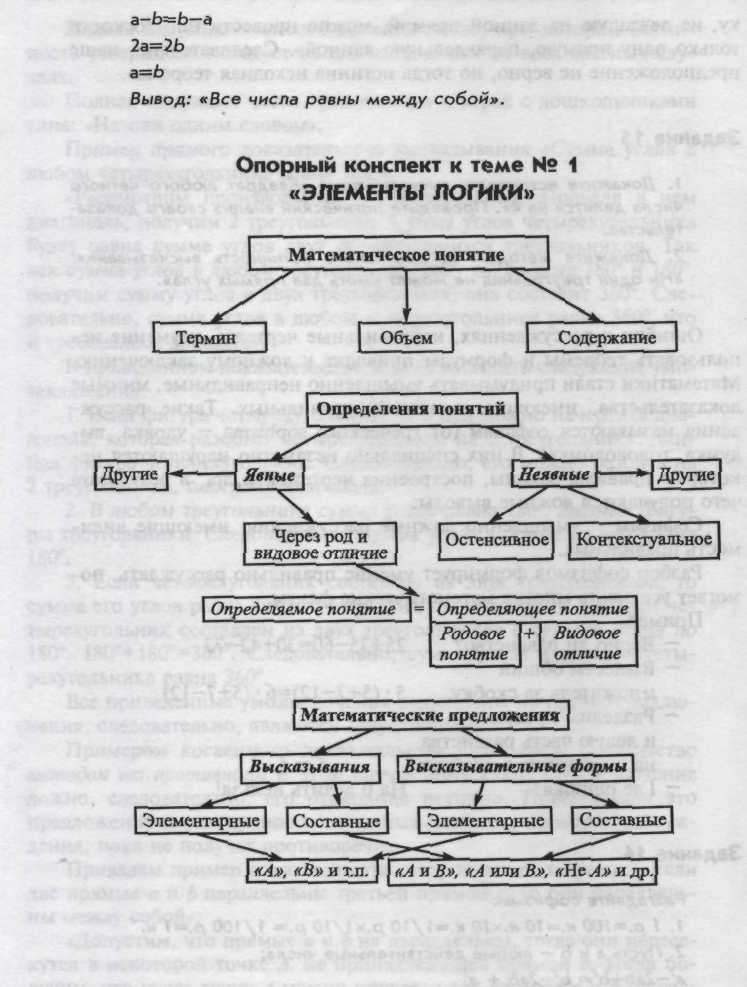
Пример прямого доказательства высказывания «Сумма углов в любом четырехугольнике равна 360°»:

«Рассмотрим произвольный четырехугольник. Проведя в нем диагональ, получим 2 треугольника. Сумма углов четырехугольника будет равна сумме углов двух образовавшихся треугольников. Так как сумма углов в любом треугольнике 180°, то, сложив 180° и 180°, получим сумму углов в двух треугольниках, она составит 360°. Сле­довательно, сумма углов в любом четырехугольнике равна 360", что и требовалось доказать».

В приведенном доказательстве можно выделить следующие умо­заключения:

1. Если фигура четырехугольник, то в ней можно начертить диа­гональ, которая разобьет четырехугольник на 2 треугольника. Дан­ная фигура четырехугольник. Следовательно, его можно разбить на 2 треугольника, построив диагональ.

2. В любом треугольнике сумма углов равна ISO". Данные фигу­ры треугольники. Следовательно, сумма углов каждого из них равна 180°.

3. Если четырехугольник составлен из двух треугольников, то сумма его углов равна сумме углов этих треугольников. Данный че­тырехугольник составлен из двух треугольников с суммой углов по 180°. 180о+180о=360°. Следовательно, сумма углов в данном четы­рехугольнике равна 360°.

Все приведенные умозаключения выполнены по правилу заклю­чения, следовательно, являются дедуктивными.

Примером косвенного доказательства является доказательство методом от противного. В этом случае допускают, что заключение ложно, следовательно, его отрицание истинно. Присоединив это предложение к совокупности истинных посылок, проводят рассуж­дения, пока не получат противоречие.

Приведем пример доказательства от противного теоремы: «Если две прямые а и Ь параллельны третьей прямой с, то они параллель­ны между собой»:

«Допустим, что прямые а и b не параллельны, тогда они пересе­кутся в некоторой точке А, не принадлежащей прямой с. Тогда по­лучим, что через точку А можно провести две прямые а и Ь, парал­лельные с. Это противоречит аксиоме параллельности: «Через точ-

8. Сформулируйте правила явного определения через род и видовое отличие.

9. Какое определение называется:

• контекстуальным;

• остенсивным?

10. Что такое высказывание, а что такое высказывательная форма?

11. Когда предложения видов «А и В», «А или В», «Не А» истинны, а когда ложны?

12. Перечислите кванторы общности и кванторы существования. Как установить значение истинности предложений с различными квантора­ми?

13. Когда между предложениями имеется отношение следования, а когда отношение равносильности? Как они обозначаются?

14. Что такое умозаключение? Какое умозаключение называется де­дуктивным?

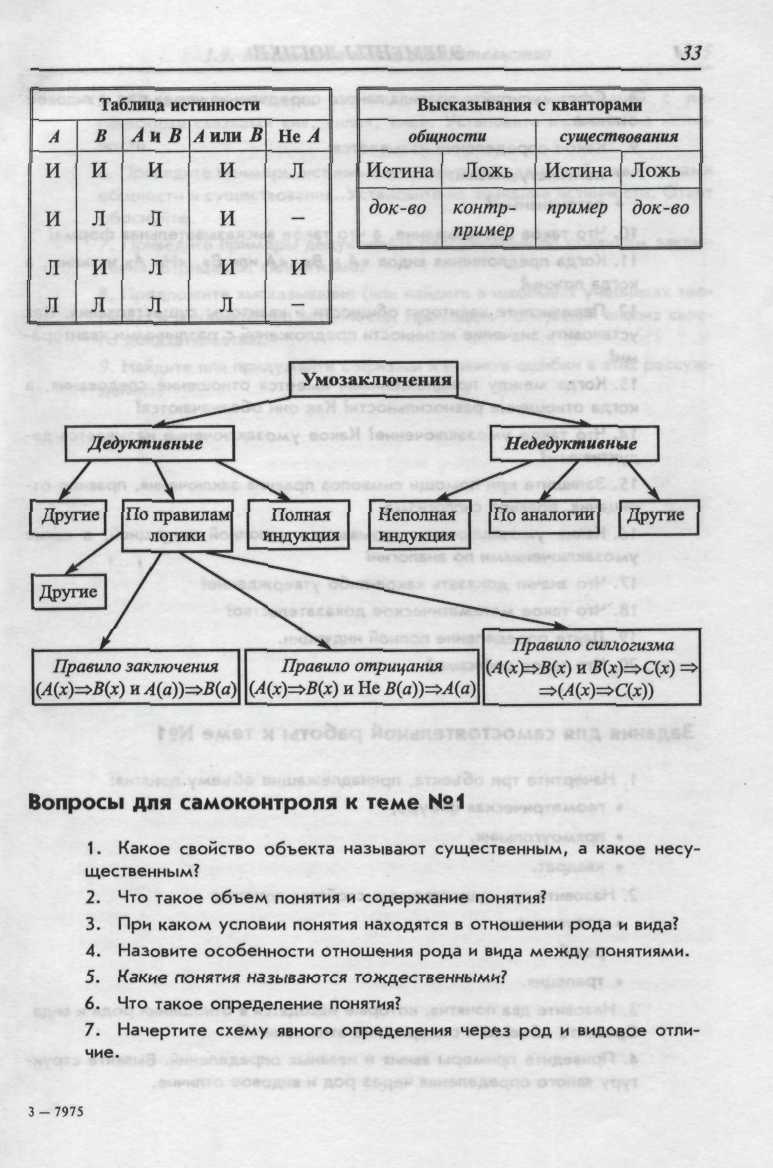
15. Запишите при помощи символов правила заключения, правило от­рицания, правило силлогизма.

16. Какие умозаключения называются неполной индукцией, а какие умозаключениями по аналогии?

17. Что значит доказать какое-либо утверждение?

18. Что такое математическое доказательство?

19. Дайте определение полной индукции.

20. Что такое софизмы?

Задания для самостоятельной работы к теме №1

1. Начертите три объекта, принадлежащие объему понятия:

• геометрическая фигура,

• прямоугольник,

• квадрат.

2. Назовите три существенных свойства понятия:

• треугольник,

• ромб,

• трапеция.

3. Назовите два понятия, которые находятся в отношении рода и вида. Сравните объемы и содержание этих понятий.

4. Приведите примеры явных и неявных определений. Выявите струк­туру явного определения через род и видовое отличие.

5. Приведите примеры истинных и ложных высказываний с ло­гическими связками «и», «или», «не». Установите их значение истин­ности.

6.Приведите примеры истинных и ложных высказываний с кванторами общности и существования. Установите их значение истинности. Ответ обоснуйте.

7. Приведите примеры дедуктивных рассуждений по правилам заклю­чения, отрицания, силлогизма.

8. Предложите высказывание (или найдите в школьных учебниках тео­рему) и докажите его истинность. Проведите логический анализ свое­го доказательства.

9. Найдите или придумайте софизмы и выявите ошибки в этих рассуж­дениях.

ТЕМА 2

ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ