Связь метода динамического программирования

С принципом максимума

Существует связь между функцией будущих потерь 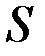и сопряженными переменными 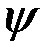. Рассмотрим задачу Лагранжа:

, , , .

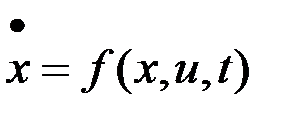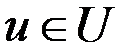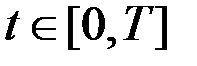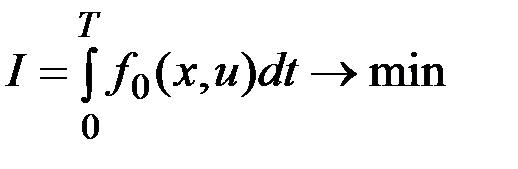Перепишем уравнение Беллмана в следующем виде

.

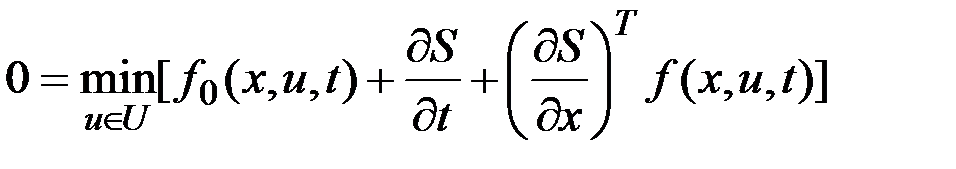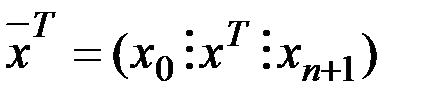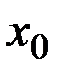Введем в рассмотрение расширенный вектор , где и 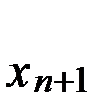определяются уравнениями

, .

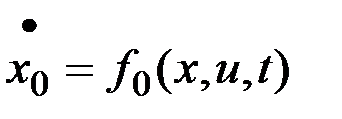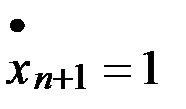Расширенная вектор-функция правых частей имеет вид:

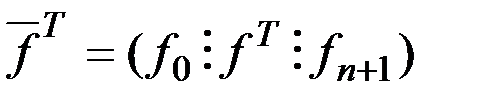, где .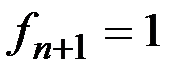

Введем вектор 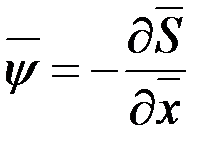, где 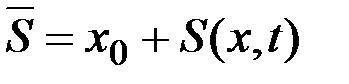, т.е.

, , .

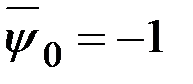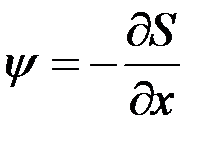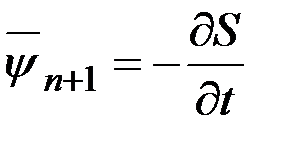Тогда уравнение Беллмана можно переписать в виде

,

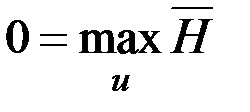где .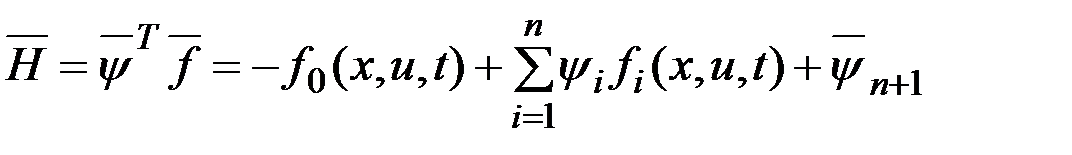

Таким образом, мы пришли к принципу максимума: оптимальное управление обеспечивает максимум гамильтониану 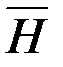, значение которого на оптимальной траектории равно нулю.

Получим каноническую систему уравнений. Уравнение для вектора может быть записано сразу: .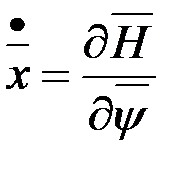

Уравнения для 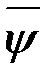получим, предположив, что функция 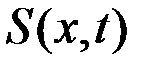дважды дифференцируема, тогда

.

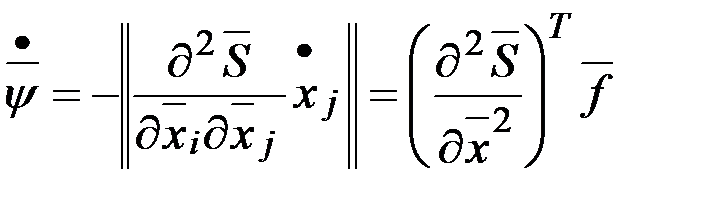Для любого фиксированного момента времени могут быть найдены оптимальные значения 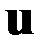, , 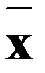для которых гамильтониан обращается в нуль. Отсюда следует, что при фиксированных 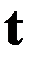и оптимальном управлении 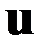величина гамильтониана достигает максимума по 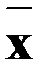в точке оптимальной траектории. Поэтому

.

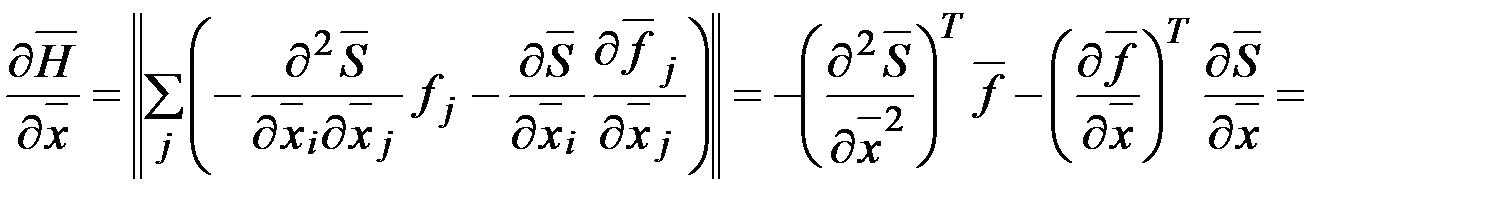
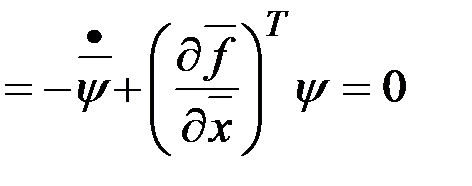Откуда получаем, что 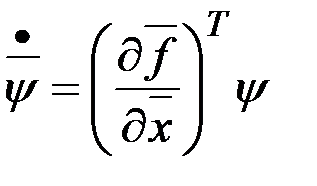, и учитывая, что 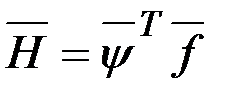, имеем: .

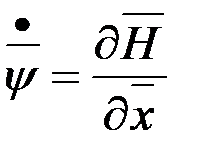Таким образом, вектор 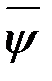, участвующий в принципе максимума, является антиградиентом функции 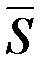, связанной с функцией будущих потерь. Уравнение Беллмана эквивалентно необходимым условиям в форме принципа максимума. Результатом решения уравнения Беллмана является оптимальное управление в форме синтеза, в то время как при использовании принципа максимума определяется лишь программа оптимального управления. Однако численно решить краевую задачу и тем самым определить программу управления проще, чем решить уравнение в частных производных, т.е. построить синтез. Аналитическое решение уравнения Беллмана можно получить лишь в некоторых частных случаях.

Связь уравнения Беллмана с уравнением Гамильтона-Якоби классического вариационного исчисления

Запишем уравнение Беллмана

.

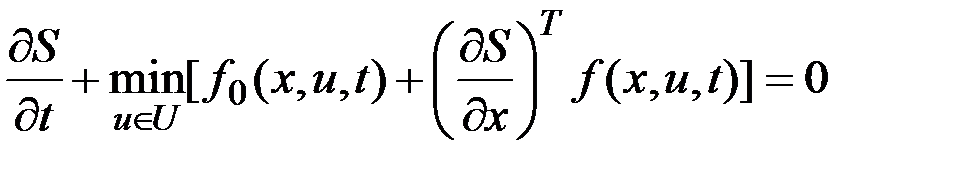Обозначим 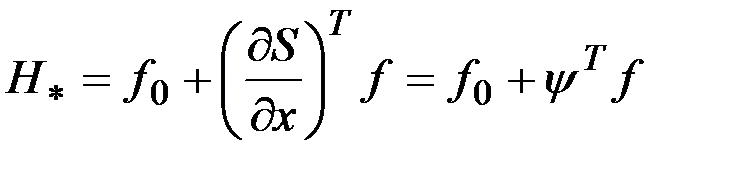. Отметим, что 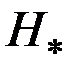отличается от гамильтониана 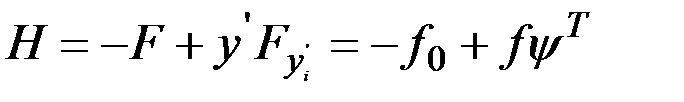только знаком перед 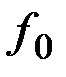. При поиске минимума эти записи гамильтониана эквивалентны. Имеем

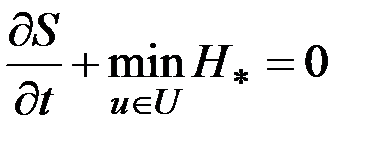- уравнение Беллмана,

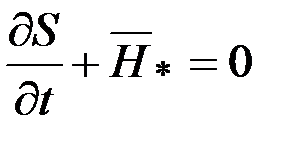- уравнение Гамильтона-Якоби.

Гамильтониан 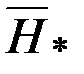содержит управление 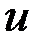, которое получалось бы из необходимого условия простого экстремума 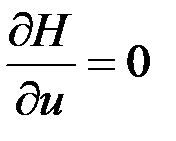. Уравнение Беллмана является развитием результатов классического вариационного исчисления, распространяющим их на системы с ограничением на управление .

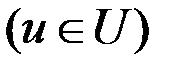Геометрическая интерпретация решения

Уравнения Беллмана

Рассмотрим решение задачи минимизации, когда функционал содержит только терминальный член: .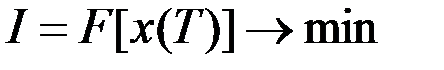

Пусть доказано существование функции Беллмана, удовлетворяющей уравнению

.

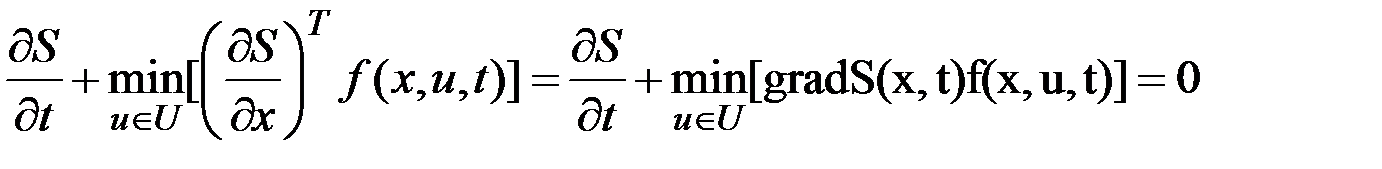Минимум скалярного произведения двух векторов, достигается, если они направлены в противоположные стороны. Поскольку 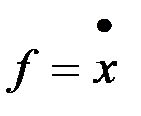, можно сделать вывод, что оптимальное движение точки должно быть направлено против градиента функции .

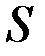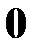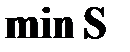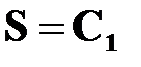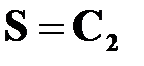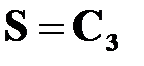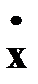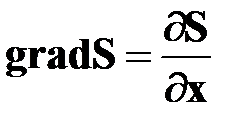Рис.4.2. Семейство линий уровней функции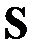

На рис. 4.2 для двухмерной задачи показано семейство линий уровней функции 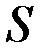и положение ее минимального значения, равного 0, а также одна из траекторий движения, приводящая к этому минимуму.