Проверка гипотез о дисперсии.

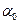А. Рассматривается нормально распределенная случайная величина .Для получена выборка из независимых наблюдений, где достаточно велико. Чтобы при заданном уровне значимости проверить основную гипотезу о равенстве неизвестной генеральной дисперсии значению , при альтернативной гипотезе : применяется статистика

где - исправленная статистическая дисперсия, вычисленная по выборке. Случайная величина имеет хи-квадрат распределение с числом степеней свободы , для заданного уровня значимости .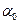

Построение области принятие гипотезы зависит от альтернативной гипотезы . Можно выделить следующие случаи:

1. Если альтернативная гипотеза имеет вид: : , то областью принятия гипотезы является интервал ( ); а полуинтервал [ ) - критической областью. Вычислив по выборке расчетное значение статистики , сравниваем с квантилем , и если , то нет оснований для отвержения основной гипотезы , если же > , то основная гипотеза отвергается.

2. Если альтернативная гипотеза : , то сравнивают с квантилем . Если > , то нет оснований отвергать основную гипотезу ; если же < , то основную гипотезу отвергают.

3. Если альтернативная гипотеза : , то областью принятия гипотезы является интервал ; а объединение полуинтервалов - критической областью. Если , то нет оснований отвергать основную гипотезу .

Б.Рассматриваются две нормально распределённые случайные величины и . Для и получены независимые выборки объемов и . По этим выборкам вычислены исправленные статистические дисперсии и . Нужно сравнить эти дисперсии.

Чтобы при заданном уровне значимости 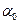проверить основную гипотезу : о равенстве генеральных дисперсий нормально распределенных случайных величин и , применяется статистика

, где > , ,

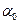имеющая -распределение Фишера-Снедокора с и степенями свободы при заданном уровне значимости . сравнивают с квантилем

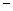
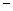-распределения ( число степеней свободы большей исправленной дисперсии), или , в зависимости от альтернативной гипотезы.

1. Если альтернативная гипотеза : и < , то нет оснований для отвержения основной гипотезы . Если > , то основную гипотезу отвергают.

2. Если альтернативная гипотеза : и < , то нет оснований для отвержения основной гипотезы ; если > , то основную гипотезу отвергают.

Задачи

3.19. В соответствии с техническими условиями среднее время безотказной работы для приборов определенного класса должно составлять в среднем 10000 часов со средним квадратическим отклонением часов. Время безотказной работы приборов подчиняется нормальному закону распределения. Из некоторой партии извлечена выборка объема приборов и по ней найдена исправленная выборочная дисперсия времени безотказной работы приборов часов. Можно ли считать, что вся партия приборов не удовлетворяет техническим условиям, если ?

Решение.Для того чтобы ответить на поставленный вопрос сформулируем основную гипотезу и альтернативную гипотезу . Уровень значимости задан. Объем выборки .

Для проверки гипотезы воспользуемся статистикой . Подставим значения , ; , найдем .

По таблице (приложение № 5), по уровню значимости и числу степеней свободы находим квантиль . Тогда интервал , определяет область принятия гипотезы, а полуинтервал, - критическую область, поскольку То нет оснований для утверждения основной гипотезы . Это значит, что партия приборов удовлетворяет техническим условиям.

Ответ:партия приборов удовлетворяет техническим условиям.

2. Известно, что добавление специальных веществ уменьшает жесткость воды. Дисперсия измерений оценки жесткости воды по 50 пробам после добавления специальных веществ равна . Требуется при уровне значимости проверить гипотезу о том, что генеральная дисперсия измерений равна предполагаемому значению:

а) ; б) .

3.20.Точность наладки некоторого класса приборов характеризуется дисперсией показания прибора. Если эта величина будет больше 120 , то прибор переналаживается. Исправленная выборочная дисперсия 25 случайных измерений прибором оказалось равной: а) б б)

Нужно ли производить наладку прибора, если уровень значимости ?

3.22. Из нормально распределенной генеральной совокупности извлечена выборка значений коэффициента трения шины по асфальту:

Значения коэффициента трения,	0,16	0,17	0,18	0,19	0,20	0,21
Частота значений коэффициента трения ,

Согласно технологии изготовления шины при определенной процедуре проверки коэффициента трения установлено, что дисперсия результатов измерений этого коэффициента равна 0,1. Требуется, при уровне значимости , проверить гипотезу о том, что дисперсия результатов измерений коэффициента трения равна 0,1.

3.23.Точность наладки станка – автомата, производящего детали, характеризуется дисперсией длины деталей. Из нормально распределенной генеральной совокупности извлечена выборка:

длина деталей,	3,1	3,2	3,3	3,4	3,5	3,6	3,7
частота,

Требуется, при уровне значимости , проверить, обеспечивает ли станок требуемую точность, если дисперсия длины деталей не должна превышать .

3.24.Фирма работает «устойчиво», если дисперсия величины прибыли не превосходит ден.ед.². Исправленная выборочная дисперсия 15 случайно отобранных фирм оказалась равной ден.ед.². Требуется, при уровне значимости , проверить гипотезу о том, что отобранные фирмы работают не устойчиво.

3.25.По двум независимым выборкам, объемов и , извлеченных из нормально распределенных генеральных совокупностей и , вычислены исправленные выборочные дисперсии и . Требуется, при уровне значимости , проверить основную гипотезу о равенстве генеральных дисперсий.

Решение:Сформулируем основную гипотезу : и альтернативную .

Уровень значимости задан .

Объемы выборок известны и .

Для проверки гипотезы применим статистику .

По таблице – распределения (приложение 7) находим квантиль . Поскольку альтернативная гипотеза : то критическая область правосторонняя 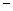, а областью принятия гипотезы является интервал . Так как =1,198< , то нет оснований для отвержения основной гипотезы . Значит, генеральные дисперсии и равны.

Ответ: .

3.26. На предприятии разработаны два метода изготовления изделия и вычислены исправленные дисперсии расхода сырья на единицу готовой продукции кг², кг² по выборкам объемов изделий и изделий. Требуется, при уровне значимости , проверить гипотезу о равенстве генеральных дисперсий нормально распределенных совокупностей расхода сырья на единицу изделия.

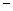
3.27. Для проверки эффективности нового лекарства были отобраны две случайные группы больных по 30 человек. Одной группе давали таблетки с прежним проверенным лекарством, а другой с новым. В первой группе исправленная дисперсия выздоровления дней, а во второй дня. Требуется, при уровне значимости , проверить гипотезу о том, что новое лекарство не более эффективное, чем прежнее.

3.28. При исследовании работы стабилизатора напряжения в самолете на стенде проведено 12 независимых испытаний:

Выходное напряжение, ,	0,21	0,24	0,28	0,30
Частота значений выходного напряжения,

В полете проведено ёще 15 испытаний стабилизатора напряжения в самолете:

Выходное напряжение, ,	0,33	0,34	0,36	0,37	0,40
Частота,

Требуется, при уровне значимости , сравнив исправленные дисперсии, ответить, есть ли основания полагать, что факторы, воздействующие на стабилизатор в полете, оказывают существенное влияние на точность его работы.

3.29. Результаты независимых измерений производительности двух агрегатов приведены в таблице:

Агрегат № 1	15,0	15,2	15,7	16,0	16,1	16,3	16,6
Агрегат № 2	14,7	15,1	15,5	15,9	16,2	16,4	16,5

Можно ли считать, что производительности обоих агрегатов равны? Требуется проверить гипотезу о равенстве генеральных дисперсий нормально распределенных совокупностей при уровне значимости .

3.30.Для сравнения качества консервов двух заводов взяты две выборки продукции этих заводов. Качество каждой банки консервов оценено в баллах при помощи органолептических показателей. Результаты оценок приведены в таблице:

Завод № 1
Завод № 2

Можно ли считать, что качество продукции одинаковое на заводах №1 и №2, сравнив исправленные дисперсии выборок при уровне значимости . Предполагается, что результаты оценок распределены нормально и выборки независимы.