Для дискретной случайной величины

, где р( ; )= Р( ). ( 2.2)

Оценка называется самостоятельной оценкой параметра , если сходится по вероятности к , при .

2. Если и при , то - состоятельная оценка параметра .

Для отыскания оценок параметров генеральной совокупности по данным выборки применяют метод наибольшего правдоподобия и метод моментов. Согласно методу наибольшего правдоподобия, оценку неизвестного параметра распределения случайной величины Х находят, решая уравнение:

или систему уравнений:

если требуется оценить m неизвестных параметров; где и - функции правдоподобия, – если -непрерывная случайная величина и если Х- дискретная случайная величина, а вероятность – функция неизвестного параметра a.

Метод моментов заключается в том, что статистические моменты выборки принимаются в качестве оценок для моментов распределения случайной величины Х и из построенных равенств статистических и теоретических моментов находят значение оценки параметра.

Точность и надежность оценки для параметра определяют рассматривая вероятность неравенства

Случайный интервал, определяемый результатами наблюдений, который с заданной вероятностью накрывает неизвестный параметр a, называется доверительным интервалом для параметра a, соответствующим доверительной вероятности .

Доверительные интервалы для математического ожидания 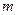нормально распределенной случайной величины Х имеют вид:

а) при неизвестном среднем квадратическом отклонении

, (2.3)

где - квантиль распределения Стьюдента (приложения 3) для заданной доверительной вероятности и числа степеней свободы 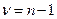находят из равенства ; - исправленная стандартная ошибка.

б) при известном среднем квадратическом отклонении :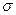

(2.4)

где - среднее арифметическое (несмещенная, эффективная и состоятельная оценка математического ожидания); – значение аргумента функции (приложения 1), находят из равенства ; - объем выборки.

Доверительные интервалы разности математических ожиданий m₁ и m₂ двух генеральных совокупностей, распределенных по нормальному закону, определяются формулами:

а) если дисперсии и известны, то

, (2.5)

где – квантиль нормального закона распределения для заданной доверительной вероятности находят из равенства ;

б) если дисперсии величина неизвестна, то

, (2.6)

где - квантиль распределения Стьюдента с числом степеней свободы находят из равенства ; - объемы выборок; - исправленные статистические дисперсии; - средние арифметические выборок.

Доверительный интервал для дисперсии выражается формулой:

(2.7)

где – исправленная статистическая дисперсия; , –квантили распределения с 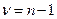степенями свободы для доверительной вероятности ; – объем выборки; средние арифметическое.

Для оценки среднего квадратического отклонения 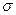нормально распределенной случайной величины Х применяется так же доверительный интервал:

(при ), (2.8)

или

(при >1), (2.9)

где значения находят по таблице 5 (приложение 5)по заданной доверительной вероятности и объеме выборки .

Если распределение генеральной совокупности не является нормальным, то в некоторых случаях по выборкам большего объема можно построить доверительные интервалы для неизвестных параметров приближенно, используя предельные теоремы теории вероятностей. Так доверительный интервал для вероятности появления события в одном испытании имеет вид:

(2.7)

где W - относительная частота появления события в испытаниях; - объем выборки; - квантиль нормального закона распределения, находят из равенства , поскольку относительная частота W по теореме Муавра-Лапласа имеет асимптотически нормальное распределение; доверительная вероятность.

Задачи

2.1. Пусть - выборка из нормально распределенной генеральной совокупности с конечными математическим ожиданием 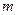и дисперсией , и пусть в качестве оценки математического ожидания 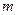генеральной совокупности предполагается взять среднее арифметическое выборки. Проверить несмещенность, эффективность и состоятельность этой оценки.

Решение.Среднее арифметическое выборки вычисляется по формуле:

.

Чтобы проверить несмещенность, эффективность и состоятельность среднего арифметического как оценки математического ожидания 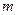генеральной совокупности, рассмотрим эту статистику как функцию - мерной случайной величины

составляющие которой имеют тот же закон распределения, что и изучаемая случайная величина Х, то есть: и причем Х_i – независимые случайные величины в совокупности. Тогда:

.

Поскольку то по определению получаем, что среднее арифметическое - несмещенная оценка и так как при то - состоятельная оценка математического ожидания 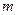генеральной совокупности.

Для проверки эффективности оценки вычислим информацию Фишера J_n(m) по формуле (2.1.). Плотность распределения вероятностей нормально распределенной случайной величины имеет вид:

(2.1.)

Прологарифмировав, получаем:

.

Частная производная по 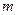равна:

.

Математическое ожидание случайной величины равно:

Подставив значение математического ожидания в (2.1.), получим:

Поскольку, , и дисперсия уменьшается с ростом n, то для нормального распределенной генеральной совокупности среднее арифметическое является эффективной оценкой математического ожидания .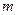

Ответ: среднее арифметическое - несмещенная, эффективная и состоятельная оценка математического ожидания.

2.2. Пусть задана выборка наблюдений случайной величины Х, распределенной по нормальному закону, и пусть в качестве оценки математического ожидания 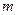генеральной совокупности предлагается взять медиану: . Проверить несмещенность, эффективность и состоятельность этой оценки.

2.3. В результате проведения N независимых экспериментов при одних и тех же условиях 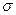случайное событие А произошло М раз. Показать, что относительная частота появления события А в N экспериментах, является несмещенной, эффективной и состоятельной оценкой вероятности Р(А) появления события А в каждом эксперименте.

2.4. Пусть в качестве оценки математического ожидания 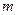генеральной совокупности предлагается взять моду , вычисленную по выборке . Проверить несмещенность, эффективность и состоятельность этой оценки.

2.5. Предположим, что произведены две случайные выборки из генеральной совокупности, распределенной по нормальному закону. И пусть вычислены средние арифметические и исправленные статистические дисперсии этих выборок. Показать, что объединенные оценки, вычисляемые по формулам:

,

будут несмещенными, эффективными и состоятельными оценками математического ожидания 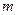и дисперсии генеральной совокупности.

2.6.Методом наибольшего правдоподобия найти оценку математического ожидания 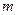и дисперсии по выборке , извлеченной из нормально распределенной генеральной совокупности.

Решение.Пусть выборка наблюдений из генеральной совокупности нормально распределенной случайной величины Х с плотностью распределения вероятностей

Составим функцию правдоподобия по формуле:

Прологарифмировав это равенство, получим:

Применив необходимые условия экстремума функции составим систему уравнений для нахождения оценок параметров :

Последовательно преобразовывая первое уравнение системы, находим оценку для :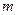

то есть оценкой

математического ожидания генеральной совокупности является среднее арифметическое выборки . Подставляя это значение 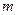во второе уравнение системы, получим:

или .

Откуда находим оценку для дисперсии генеральной совокупности:

Отметим, что среднее арифметическое является несмещенной, эффективной и состоятельной оценкой математического ожидания нормально распределенной генеральной совокупности, а статистическая дисперсия является состоятельной и смещенной оценкой дисперсии . Поэтому, чтобы получить несмещенную оценку дисперсии, умножают дисперсию на множитель

2.7. Методом наибольшего правдоподобия найти оценку параметра распределения Пуассона по выборке .

2.8. Пусть - вероятность появления события а - дискретная случайная величина, заданная частотным рядом распределения (таблица 2.1). Методом наибольшего правдоподобия найти оценку параметра и вычислить ее значение по выборке; заданной в таблице 2.1:

Таблица 2.1

Решение. Случайная величина является дискретной случайной величиной, имеющей биномиальный закон распределения. Тогда вероятность того, что случайная величина приняла значение ,равна , где может принимать неотрицательные целочисленные значения от 0 до : Составим функцию правдоподобия для выборки:

			…
			…

Прологарифмируем эту функцию:

.

Применяя необходимое условие экстремума, получим уравнение

,

решив которое, последовательно найдем оценку p:

, .

Тогда для заданной выборки оценка вероятности появления события равна:

.

Ответ: p=0,081.

2.9.Предположим, что число автомашин, подъезжающих на заправку в течение n часов, описывается случайной величиной, имеющей закон распределения Пуассона с параметром , где – возможное число автомашин подъезжающих на заправку в течении одного часа. Методом наибольшего правдоподобия найти оценку параметра .

2.10.Производится n независимых испытаний, в каждом из которых событие А может произойти с вероятностью р. Предположим, что событие А может произойти в m испытаниях. Методом наибольшего правдоподобия найти оценку вероятности p появления события A в каждом испытании.

2.11. Методом наибольшего правдоподобия найти оценку параметра λ по выборке из генеральной совокупности, распределенной по показательному закону:

2.12. Пусть выборка наблюдений случайной величины X, имеющей распределение Пуассона с неизвестным параметром :

.

Методом наибольшего правдоподобия найти оценку параметра .

2.13. Пусть случайная величина X распределена по показательному закону с плотностью вероятностей

и неизвестным параметром λ, λ>0.

Методом моментов найти оценку неизвестного параметра λ по выборке

			…
			…

Решение. Вычислим начальный момент первого порядка, применив формулу интегрирования по частям

Поскольку статистический начальный момент первого порядка равен

то приравнивая значения этих двух моментов, получим:

Откуда находим .

Ответ: .

2.14. В n независимых испытаниях событие А произошло m раз. Методом моментов найти оценку вероятности p появления события A в одном испытании.

2.15. Методом моментов по выборке объема n найти оценку параметров m и нормально распределенной случайной величины X.

2.16. Методом моментов по выборке объема n найти оценку параметра случайной величины X, имеющей Пуассоновское распределение: .

2.17. Выборка из большей партии электроламп содержит n=49 ламп. Средняя продолжительность горения лампы выборки оказалась равной ч. Найти с надежностью α=0,95 доверительный интервал для средней продолжительности m горения лампы всей партии, если известно, что среднее квадратическое отклонение продолжительности горения лампы .

Решение. Воспользуемся доверительным интервалом для средней продолжительности m горения лампы при известном среднем квадратическом отклонении 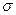(формула 2.4.):

(2.8)

Средняя продолжительность горения лампы выборки ч, объем выборки n=50 ламп. По заданной доверительной вероятности α=0,95, из равенства , , по таблице (приложение 2), находим . Подставив значения , , , n=49 в (2.4), получим:

.

Вычислив, окончательно находим доверительный интервал:

496,08<m<503,92

Ответ: 496,08<m<503,92.

2.18. Для проверки износоустойчивости шин фирмы «Белшина» из большой партии было отобрано 100 шин. Средняя продолжительность эксплуатации одной шины оказалась равной 81 тыс. км. Найти с надежностью α=0,95 доверительный интервал для средней продолжительности m эксплуатации шин всей партии, если известно, что среднее квадратическое отклонение продолжительности эксплуатации одной шины 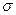=9 тыс. км.

2.19. Для проверки средней дневной выработки рабочих строительной организации было проведено обследование выработки 50 рабочих. Средняя выработка одного рабочего оказалась равной 3,95 м², а среднее квадратическое отклонение 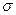=0,75 м². Найти с надежностью α=0,95 доверительный интервал для средней выработки одного рабочего всей строительной организации.

2.20. Из партии поршневых колец изготовленных за смену, извлечена выборка объеме n=100 и вычислено среднее арифметическое диаметров изготовленных поршневых колец. Найти с надежностью α=0,95 доверительный интервал для математического ожидания диаметра поршневых колец изготовленных за смену.

2.21. Найти минимальный объем выборки, при котором с надежностью α=0,99 точность оценки математического ожидания m генеральной совокупности времени безотказной работы электронной лампы по известному среднему арифметическому, будет равно δ=0,5, если известно среднее квадратическое отклонение 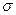=10 часов нормально распределенной генеральной совокупности.

Решение.Воспользуемся формулой, определяющей точность оценки математического ожидания, нормально распределенной генеральной совокупности по известному среднему квадратическому:

,

откуда следует, что .

Из условия задачи известно: 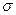=10, δ=0,5. Найдем . Пользуясь таблицей (приложение 2), по доверительной вероятности α=0,99 из равенства , находим . Подставив , 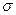=10, δ=0,5, получим:

Ответ: n=27.

2.22. Найти минимальный объем выборки, при котором с надежностью α=0,95 точность оценки математического ожидания нормально распределенной генеральной совокупности емкостей конденсаторов по известному среднему арифметическому выборки, будет равно 0,3, если известно среднее квадратическое отклонение, 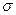=5 мкФ, нормально распределенной генеральной совокупности.

2.23. Для обследования средней урожайности ячменя с одного гектара по области проведено выборочное обследование участков посевных площадей, результаты которого приведены в таблице 2.2:

Таблица 2.2

Урожайность пшеницы,
Число участков,

Оценить с надежностью α=0,95 математическое ожидание m и дисперсию нормально распределенной генеральной совокупности по среднему арифметическому и статистической дисперсии при помощи доверительного интервала.

Решение. Вычислим среднее арифметическое и исправление среднее статистическое квадратическое отклонение соответственно по формулам:

;

По доверительной вероятности α=0,95 и числу степеней свободы находим квантиль распределения Стьюдента (приложение 3) . Доверительный интервал для математического ожидания найдем по формуле:

.

Подставив значения ; ; ; , последовательно находим доверительный интервал:

, ,

содержащий математическое ожидание m генеральной совокупности с надежностью α=0,95. Для построения доверительного интервала для дисперсии воспользуемся формулой (2.7). Для доверительной вероятности α=0,95 и числа степеней свободы по таблице (приложение 4) находим квантили хи-квадрат распределения

.

Подставив значения ; и ; в формулу доверительного интервала (2.7.), получим

или .

Доверительный интервал для среднего квадратического отклонения (2.8) после подстановки найденного по таблице (приложение 5), принимает вид: или

Ответ:

2.24. Для исследования времени средней продолжительности безотказной работы телевизионных трубок, произведенных на заводе «Горизонт» было проведено выборочное обследование 100 телевизионных трубок. Оказалось, что среднее время безотказной работы равно 36 месяцев со среднем квадратическом отклонении равным 4 месяца. Постройте 95%-ные и 99%-ные доверительные интервалы для среднего времени безотказной работы телевизионных трубок, произведенных на заводе «Горизонт».

2.25. Предельная нагрузка для выборки из 50 стальных стержней характеризуется выборкой:

Постройте доверительные интервалы для оценки с надежностью α=0,95 средней предельной нагрузки и среднего квадратического отклонения предельной нагрузки стальных стержней партии, из которой произведена выборка.

2.26. Для наблюдений каждой из пяти случайных выборок постройте с надежностью α=0,95 доверительные интервалы для оценки математического ожидания генеральной совокупности и дисперсии:

1) Выборка сопротивлений:

	0,27	0,28	0,29	0,30	0,31	0,32

2) Диаметры шаров в шарикоподшипниках:

	1,97	1,98	1,99	2,00	2,01	2,02

3) Увеличение частоты пульса студентов после занятий физкультурой:

4) Процентное содержание витамина С в выборке витаминных драже:

	12,9	14,3	14,8	15,2	16,3

5) Рост студентов 1-го и 2-го курсов университета

	1,63	1,68	1,70	1,71	1,73	1,80	1,87

2.27. Из большой партии микросхем одного типа были случайно отобраны и проверены 100 штук. У 16 микросхем обнаружились отклонения технических характеристик. Найти 95%-ный доверительный интервал для вероятности того, что микросхема будет бракованной во всей партии. Какой минимальный объем выборки следует взять, для того, чтобы с вероятностью 0,95 можно было утверждать, что вероятность появления бракованных микросхем в выборке не более чем 1%.

Решение. Эффективной оценкой вероятности появления события в одном испытании является относительная частота появления события в n испытаниях. По теореме Муавра-Лапласа относительная частота W имеет асимптотически нормальное распределение, поэтому доверительный интервал для вероятности того, что некоторая микросхема во всей партии будет бракованной имеет вид (2.10). Вычислив относительную частоту и найдя по таблице 1 (приложение 1) квантиль нормального распределения из равенства , построим доверительный интервал:

или

.

Для определения минимального объема выборки представим доверительный интервал (2.10) в виде неравенства

,

которое выполняется с вероятностью α=0,95. Так как по условию задачи , то для определения получим неравенство

.

Последовательно преобразуя неравенство, находим :

Ответ:Доверительный интервал минимальный объем выборки =3820.

2.28. С производственной линии, производящей часы, было отобрано 100 часов, 10 из которых содержали брак. Найти 95% доверительный интервал для вероятности того, что случайно отобранные часы с производственной линии будут содержать брак. Какой минимальный объем выборки следует взять для того, чтобы с вероятностью 0,95 можно было утверждать, что вероятность появления бракованных часов на производственной линии отличается от частоты появления бракованных часов в выборке не более чем на 5%?

2.29. Для определения в схожести семян в партии пшеницы было отобрано 1000 зерен, из которых взошло 980. Найти 99% доверительный интервал для вероятности того, что случайно отобранное зерно пшеницы из партии взойдет. Найти минимальный объем выборки, на основании которого можно утверждать, что вероятность того, что случайно отобранное зерно пшеницы из партии взойдет, отличается от частоты всхожести семян пшеницы не более чем на 3%.

2.30. Для предварительного опроса населения города N в связи с избирательной компанией была произведена выборка 1000 избирателей из которых 350 заявили, что они проголосуют за кандидата от оппозиции. Найти 95% доверительный интервал для вероятности того, что случайно отобранный избиратель города N проголосует за кандидата от оппозиции. Какой минимальный объем выборки следует взять, для того, чтобы с вероятностью 0,99 можно было утверждать, что вероятность того, что избиратель в городе N проголосует за кандидата от оппозиции отличается от частоты избирателей в выборке которые проголосуют за кандидата от оппозиции, не более чем на 2%.

2.31. При осмотре 50 изделий из партии обнаружено 5 содержащих дефект. Найти 99% доверительный интервал для вероятности того, что случайно взятое изделие из партии будет дефектно.

2.32. Предположим, что число сбоев компьютеров за месяц имеет распределение Пуассона с параметром λ. Исследование работы 100 компьютеров показало, что среднее число сбоев за месяц равно 1,7. Найти 95% доверительный интервал для параметра λ.

Указание. Воспользоватьс