Вычисление арифметических выражений.
ЛЕКЦИЯ 1
Вычисление арифметических выражений.
1. Вычисления в среде MATLAB возможны в режиме командной строки (готовность системы к работе – знак >>) (см. рис. 1.1).

Рис. 1.1. Упрощенный интерфейс в системе MATLAB.
При работе с MATLAB в командном режиме действует простейший строчный редактор. Его команды перечислены в таблице.1.1.
Таблица 1.1. Команды строчного редактора MATLAB.
| Комбинация клавиш | Назначение |
| ® или Ctrl+b | Перемещение курсора вправо на один символ |
| или Ctrl+f | Перемещение курсора влево на один символ |
| Ctrl+® или Ctrl+r | Перемещение курсора вправо на одно слово |
| Ctrl+ или Ctrl+l | Перемещение курсора влево на одно слово |
| Home или Ctrl+a | Перемещение курсора в начало строки |
| End или Ctrl+e | Перемещение курсора в конец строки |
| и ¯ или Ctrl+р и Ctrl+n | Перелистывание предыдущих команд вверх или вниз для подстановки в строку ввода |
| Del или Ctrl+d | Стирание символа справа от курсора |
| или Ctrl+h | Стирание символа слева от курсора |
| Ctrl+k | Стирание до конца строки |
| Esc | Очистка строки ввода |
| Ins | Включение/выключение режима вставки |
| PgUp | Перелистывание страниц сессии вверх |
| PgDn | Перелистывание страниц сессии вниз |
Обратите особое внимание на применение клавиш курсора «вверх» и «вниз». Они используются для подстановки после маркера строки ввода >> ранее введенных строк, например с целью их исправления, дублирования или дополнения. При этом указанные клавиши обеспечивают перелистывание ранее введенных строк снизу вверх или сверху вниз. Такая возможность существует благодаря организации специального стека, хранящего строки с исполненными ранее командами.
2. Вычисления в среде MATLAB возможны в текстовых файлах с расширением .m (так называемые М-файлы, см. рис. 1.2). М-файлы могут быть созданы либо с помощью редактора М-файлов MATLAB, либо в другом редакторе, например Microsoft Word (с присвоением в дальнейшем этому файлу расширения .m). Последний подход является более эффективным, чем работа в командной строке MATLAB, особенно для задач, выполнение которых требует большого объема команд.

Рис.1.2. Окно редактора с текстом М-файла
М-файлы бывают двух типов: файл-программы (Script M-Files), содержащие последовательность команд и не имеющие входных и выходных аргументов, и файл-функции (Function M-Files), в которых описываются функции, определяемые пользователем.
Константы и переменные
Системные переменные.
Другие виды констант (помимо рассмотренных выше безымянных) в системе MATLAB принято называть системными переменными, поскольку с одной стороны, они задаются системой при ее загрузке, а с другой – могут переопределяться. Основные системные переменные, применяемые в системе MATLAB, перечислены ниже:
i или j – мнимая единица (квадратный корень из числа -1);
pi – число 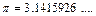 (см., например, рис. 1.1.2);
(см., например, рис. 1.1.2);
eps – погрешность операций над числами с плавающей точкой ( 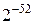 );
);
realmin – наименьшее число с плавающей точкой ( 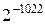 );
);
realmax – наибольшее число с плавающей точкой ( 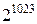 );
);
inf – значение машинной бесконечности;
ans – переменная, хранящая результат последней операции и обычно вызывающая его отображение на экране монитора (см. рис. 1.1.2);
NaN – указание на нечисловой характер данных (Not-a-Number; неопределенность).
Итак, имеем (в режиме командной строки):
| >> eps ans = 2.2204e-16 >> realmin ans = 2.2251e-308 >> realmax ans = 1.7977e+308 >> 5/0 ans = Inf >> 0/0 ans = NaN |
Следует еще раз отметить, что системные переменные могут переопределяться. Так, можно задать системной переменной eps иное значение, например, eps=0.001. Тем не менее, значения системных переменных по умолчанию задаются сразу после загрузки системы, в связи с чем системные переменные, в отличие от обычных переменных, никогда не могут быть неопределенными.
Символьная константа – это цепочка (последовательность) символов, заключенных в апострофы, например (в режиме командной строки):
| >> 'Пример символьной константы' ans = Пример символьной константы >> 'Hello' ans = Hello >> '5+5+7' ans = 5+5+7 |
Отметим, что даже если в апострофы заключается математическое выражение, оно не вычисляется и рассматривается просто как цепочка символов. В частности, в последнем примере '5+5+7' не будет возвращать число 17. Вместе с тем, с использованием специальных функций преобразования символьные выражения могут быть преобразованы в вычисляемые.
Переменные.
Переменные – это имеющие имена объекты, способные хранить некоторые, обычно разные по значению, данные (распространные объекты как в математике, так и в программировании). В общем смысле переменная – это область памяти, к которой можно обратиться
В большинстве языков программирования (например, в C/C++, Pascal, Java и др.) для использования переменной необходимо ее предварительно объявить, указав при этом к какому типу она относится. В MATLAB подобное делать не нужно, переменной можно сразу присваивать значение.
Для задания переменным определенных значений в M-языке используется операция присваивания, вводимая знаком равенства: ):
| Имя_переменной = Выражение |
Так, например, имеем (в режиме командной строки):
| >> a=5 a = |
Типы переменных заранее не декларируются, а определяются выражением, значение которого присваивается переменной.
Имя переменной (идентификатор переменной) может содержать сколь угодно символов, однако запоминается и идентифицируется лишь 31 начальный символ. Имя любой переменной не должно совпадать с именами других переменных, функций и процедур системы (иными словами, имя переменной должно быть уникальным). Имя должно начинаться с буквы английского алфавита, может содержать буквы английского алфавита, цифры и символы подчеркивания ( _ ). Запрещается включать в имена переменных пробелы и специальные символы (например +, _, *, / и т.д.). Некоторые специалисты рекомендуют использовать содержательные имена для обозначений переменных, например displ_1 для переменной, обозначающей перемещение первой точки.
Отметим, что в системе MATLAB могут использоваться символьные переменные, причем соответствующие символьные выражения заключаются в апострофы, например (в режиме командной строки):
| >> c='Sample' c = Sample |
Арифметические операции.
Система MATLAB допускает использование традиционных знаков арифметических операций, некоторые простейшие бинарные (двухоперандные) из которых (для скалярных операндов (величин)) указаны в таблице 1.3.
Таблица.1.3. Знаки некоторых простейших арифметических операций (для скалярных операндов) в системе MATLAB.
| Символ (оператор) | Выполняемое действие (описание) |
| + (оператор сложения) | Вычисляется сумма скалярных операндов (бинарный оператор) |
| – (оператор вычитания) | Вычисляется разность скалярных операндов (бинарный оператор) |
| * (оператор умножения) | Вычисляется произведение скалярных операндов (бинарный оператор) |
| / (оператор деления) | Вычисляется частное от деления скалярных операндов (бинарный оператор) |
| ^ (оператор возведения в степень) | Вычисляется возведение первого скалярного операнда в степень, определяемую вторым скалярным операндом (бинарный оператор) |
В качестве простейшего примера имеем (в режиме командной строки):
| >> x=1.2 x = 1.2000 >> y=-3.4 y = -3.4000 >> z=+0.1 z = 0.1000 >> Res1=x+y+z Res1 = -2.1000 >> Res2=x-y Res2 = 4.6000 >> Res3=x*y Res3 = -4.0800 >> Res4=x/y Res4 = -0.3529 >> Res5=x^y Res5 = 0.5380 |
Поясним, что символ «-» указанный при задании значения переменной y называется унарный минус, а символ «+» указанный при задании значения переменной z называется унарный плюс (при вводе и выводе значений, как правило, опускается).
Арифметические выражения.
Центральным понятием всех математических систем и соответствующих языков программирования является арифметическое выражение (математическое выражение).
Арифметическое выражение задает то, что должно быть вычислено в численном (реже символьном) виде. В таблице 1.6. ниже приведены примеры простейших арифметических выражений, записанных по правилам системы MATLAB и по общематематическим правилам.
Таблица 1.6. Некоторые примеры простейших арифметических выражений, записанных по правилам системы MATLAB и по общематематическим правилам.
| Выражение, записанное по правилам системы MATLAB | Выражение, записанное по общематематическим правилам |
| 5+7; | 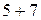 |
| 2^5*sqrt(y)/3; | 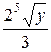 |
| 2.5*sin(x); | 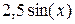 |
| 7+exp(3)/5; | 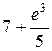 |
Разница в записях, представленных в таблице 1.6. достаточно очевидна. В системе MATLAB арифметические выражения записываются в виде одной строки, причем вместо запятой в качестве разделителя целой и дробной частей числа используется точка (а никак не запятая!). Арифметические выражения строятся на основе чисел, констант, переменных, операторов и разных спецзнаков. Специфика системы MATLAB состоит в том, что арифметические выражения задаются в виде одной строки. Так, например, 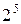 записывается как 2^5. Знак «;» (точка с запятой) в конце строки блокирует вывод результата вычислений, однако системная переменная ans позволяет вывести результат вычислений (в режиме командной строки):
записывается как 2^5. Знак «;» (точка с запятой) в конце строки блокирует вывод результата вычислений, однако системная переменная ans позволяет вывести результат вычислений (в режиме командной строки):
| >> 2^5; >> ans ans = |
Пример. Требуется вычислить следующие арифметические выражения:
1) 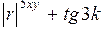 при
при 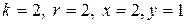
2) 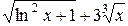 при
при 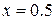
3) 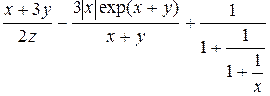 при
при 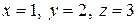
4) 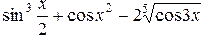 при
при 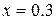
Текст М-файла.
| k=2;r=2;x=2;y=1; r1=abs(r)^(5*x*y)+tan(3*k) x=.5; r2=sqrt(log(x)^2+1)+3*x^(1/3) x=1; y=2; z=3; r3=(x+3*y)/(2*z)-3*abs(x)*exp(x+y)/(x+y)+1/(1+1/(1+1/x)) x=0.3; r4=sin(x/2)^3+cos(x^2)-2*cos(3*x)^(1/5) |
Результаты расчета в командном окне:
r1 =
1.0237e+003
r2 =
3.5978
r3 =
-18.2522
r4 =
-0.8193
Следует обратить внимание, что для просмотра результатов работы оператора знак «;» не ставится.
Варианты заданий.
Требуется запрограммировать в системе MATLAB (на M-языке) вычисление следующих арифметических выражений:
| 1. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 2. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  | |
| 3. | 1) |  | при  , ,  , ,  , ,  |
| 2) |  | при  , ,  | |
| 3) |  | при  | |
| 4) |  | при  , ,  , ,  , ,  | |
| 4. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 5. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  , ,  | |
| 4) |  | при  | |
| 6. | 1) |  | при  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  , ,  | |
| 7. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  | |
| 8. | 1) |  | при  , ,  |
| 2) |  | при  , ,  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 9. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  | |
| 10. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 11. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  | |
| 12. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 13. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  | |
| 14. | 1) |  | при  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 15. | 1) |  | при  , ,  |
| 2) |  | при  , ,  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  | |
| 16. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 17. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  , ,  , ,  | |
| 4) |  | при  , ,  | |
| 18. | 1) |  | при  , ,  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  | |
| 4) |  | при  , ,  , ,  , ,  | |
| 19. | 1) |  | при  , ,  , ,  , ,  |
| 2) |  | при  , ,  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 20. | 1) |  | при  , ,  , ,  |
| 2) |  | при  , ,  | |
| 3) |  | при  | |
| 4) |  | при  | |
| 21. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 22. | 1) |  | при  , ,  , ,  , ,  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 23. | 1) |  | при  , ,  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  | |
| 24. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  , ,  | |
| 4) |  | при  , ,  , ,  , ,  | |
| 25. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  , ,  | |
| 4) |  | при  , ,  , ,  | |
| 26. | 1) |  | при  , ,  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 27. | 1) |  | при  , ,  |
| 2) |  | при  | |
| 3) |  | при  | |
| 4) |  | при  , ,  | |
| 28. | 1) |  | при  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  | |
| 29. | 1) |  | при  , ,  , ,  , ,  , ,  , ,  |
| 2) |  | при  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  | |
| 30. | 1) |  | при  , ,  , ,  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  , ,  , ,  , ,  | |
| 4) |  | при  , ,  | |
| 31. | 1) |  | при  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  , ,  , ,  | |
| 4) |  | при  | |
| 32. | 1) |  | при  , ,  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  , ,  | |
| 33. | 1) |  | при  |
| 2) |  | при  , ,  | |
| 3) |  | при  , ,  , ,  | |
| 4) |  | при  , ,  | |
| 34. | 1) |  | при  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  , ,  | |
| 4) |  | при  , ,  | |
| 35. | 1) |  | при  , ,  , ,  |
| 2) |  | при  , ,  , ,  | |
| 3) |  | при  , ,  , ,
|
