Вероятность появления хотя бы одного события

Пусть события А₁, А₂, …, А_n независимы в совокупности, причем Р(А₁)=р₁, … , Р(А_n)= р_n.

И пусть в результате испытания могут наступить все события, либо часть из них, либо ни одно из них.

(5.1.11)

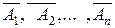Вероятность наступления события А, состоящего в появлении хотя бы одного из событий А₁, А₂, …, А_n, равна разности между единицей и произведением вероятностей противоположных событий (q₁, q₂, … q_n):

Р(А)=1 – q₁·q₂·…·q_n.

В частности, если все n событий имеют одинаковую вероятность p, то вероятность появления хотя бы одного из них

Р(А)=1 – qⁿ.

Пример 5.1.26. Вероятности полной распродажи данного товара в двух магазинах соответственно равны: Р(А₁)=0,7 и Р(А₂)=0,8. Найти вероятность полной распродажи данного товара хотя бы одним магазином (событие А).

○События А₁ и А₂ независимы, поэтому

Р(А)=1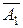–Р( )Р( 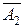)=1–0,3·0,7=0,94.●

Формула полной вероятности. Формула Байеса

Формула полной вероятности

(5.1.12)

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р(А)=Р(В₁)Р_В1(А)+ Р(В₂)Р_В2(А)+…+Р(В_n)Р_Вn(А).

Пример. 5.1.24. Для приема зачета преподаватель заготовил 50 задач: 20 задач по теории вероятностей, 30 – по математической статистике. Для сдачи зачета студент должен решить первую же доставшуюся ему наугад задачу. Какова вероятность того, что студент сдаст зачет, если он умеет решать 18 задач по теории вероятностей и 15 задач по математической статистике?

○Вероятность получить задачу по теории вероятностей (событие В₁) равна Р(В₁)=20/50=0,4, по математической статистике (событие В₂) – Р(В₂)=30/50=0,6. Если событие А состоит в том, что задача решена, то Р_В1(А)=18/20=0,9, Р_В2(А)=15/30=0,5. Тогда, используя формулу полной вероятности, получим

Р(А)=0,4·0,9+0,6·0,5=0,36+0,3=0,66.●

Формула Байеса

Пусть событие А может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … В_n, которые образуют полную группу событий. Если событие А уже произошло, то вероятности событий могут быть переоценены по формуле Байеса:

(5.1.13)

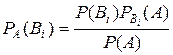
Пример 5.1.25. Для приема зачета преподаватель заготовил 50 задач: 20 задач по теории вероятностей, 30 – по математической статистике. Для сдачи зачета студент должен решить первую же доставшуюся ему наугад задачу. Студент умеет решать 18 задач по теории вероятностей и 15 задач по математической статистике. Известно, что студент сдал зачет. Какова вероятность того, что студенту досталась задача по теории вероятностей.

○В примере 1.2.24. найдено, что вероятность получить задачу по теории вероятностей (событие В₁) равна Р(В₁)=0,4, по математической статистике (событие В₂) – Р(В₂)=0,6, 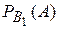=0,9, Р(А)=0,66, где А состоит в том, что задача решена. Тогда вероятность того, что студенту досталась задача по теории вероятностей

●

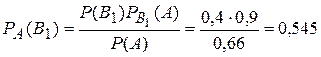Повторные независимые испытания

Формула Бернулли

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна

(5.1.14)

,

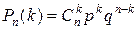где q – вероятность ненаступления события, т.е. вероятность противоположного события.

Пример 5.1.25. На экзамене 20 билетов. Какова вероятность вытянуть один и тот же билет для 3 студентов, если экзаменатор тут же кладет вытянутый билет обратно?

○ .●

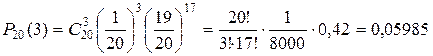Вероятность того, что в n независимых испытаниях

а) событие наступит менее k раз: ;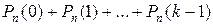

б) событие наступит более k раз: ;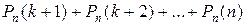

в) не менее k раз: ;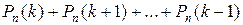

г) не более k раз: .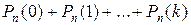

Формула Пуассона

Предположим, что мы хотим вычислить вероятность 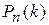появления события А при большом числе испытаний n, например, 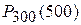. В этом случае непосредственное вычисление по формуле Бернулли значительно усложняется, тем более, если учесть, что р может быть очень малым, например

.

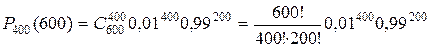Конечно, расчеты могут быть произведены с помощью компьютера, например, с использованием MS Excel. Однако, существует более простая приближенная формула – формула Пуассона.

Если вероятность р постоянна и мала, число испытаний п велико и число l= пр – незначительно (будем полагать, что l= пр£10), то вероятность 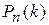того, что событие А появится k раз в п независимых испытаниях можно приближенно (тем точнее, чем больше п) найти по формуле Пуассона:

(5.1.15)

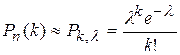
В приложении 3 приведены значения функции Пуассона .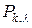

Пример 5.1.26. На факультете учится 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?

○Вероятность того, что день рождения студента 1 сентября, равна р=1/365. Так как р=1/365 – мала, n=1825 – велико и l=пр=1825·(1/365)=5£10, то применяем формулу Пуассона (5.1.15.):

Р₄(5)»Р_4,5=0,1755 (по приложению 3)●