Конспект 1. Элементы теории вероятностей

Конспект 1. Элементы теории вероятностей

Основные понятия теории вероятностей

Предмет теории вероятностей. Понятие случайного события. Виды случайных событий

Опыт, эксперимент, наблюдение явления называется испытанием. Испытаниями являются, например, бросание монеты или проведение лотереи.

Результат, исход испытания называется событием. Событиями являются: выпадение герба или цифры при подбрасывании монеты, выигрыш или проигрыш в лотерею.

Пример 5.1.1.

1)Стрелок стреляет по мишени, разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область мишени – событие.

2)В ящике имеются цветные шары. Из ящика наудачу берут один шар. Извлечение шара из ящика есть испытание. Появление шара определенного цвета – событие.

Для обозначения событий используются заглавные буквы латинского алфавита: А, В, С и т.д.

Событие А называется достоверным, если в данном испытании оно является единственно возможным его исходом.

Событие А называется невозможным, если в данном испытании оно заведомо не может произойти.

Событие А называется случайнымесли в результате испытания оно может либо произойти, либо не произойти.

Пример 5.1.2.

1) Имеется карандаш черного цвета. Начертить им черную линию – событие достоверное, начертить красным – невозможное.

2) Брошена монета. Она может упасть так, что сверху будет либо «герб», либо цифра. Поэтому событие «При бросании монеты выпал «герб» – случайное.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.

Рассмотрим основные виды случайных событий.

События называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании.

События называют несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Пример 5.1.3. Нарисовать черным и нарисовать карандашом – совместные события. Нарисовать одним карандашом одновременно и черным и красным – несовместные.

Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит. Событие, противоположное событию А, обозначают через .

Пример 5.1.4. Выпадение герба и выпадение цифры при однократном бросании монеты – противоположные события.

События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Пример 5.1.5. Появление герба и цифры при бросании монеты являются равновозможными событиями. Появление каких-либо из числа очков от 1 до 6 на брошенном игральном кубике – также равновозможные события.

Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие.

В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

Пример 5.1.6.

1) Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: «выигрыш выпал на первый билет и не выпал на второй», «выигрыш не выпал на первый билет и выпал на второй», «выигрыш выпал на оба билета», «на оба билета выигрыш не выпал». Эти события образуют полную группу попарно несовместных событий.

2) Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: «попадание», «промах». Эти два несовместных события образуют полную группу.

Свойства вероятности.

Свойство 1. Вероятность достоверного события равна 1.

□Действительно, достоверному событию благоприятствуют все n элементарных событий, т.е. m=n и, следовательно, Р(А)=m/n=n/n=1.■

Свойство 2. Вероятность невозможного события равна 0.

□В самом деле, невозможному событию не благоприятствует ни одно из элементарных событий, т.е. m=0, откуда Р(А)=m/n=0/n=0.■

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

□Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий, значит, 0<m<n, 0/n<m/n<n/n, 0<m/n<1.■

Таким образом, вероятность любого события 0 £ Р(А) £ 1.

Формула полной вероятности

(5.1.12)

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … В_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

Р(А)=Р(В₁)Р_В1(А)+ Р(В₂)Р_В2(А)+…+Р(В_n)Р_Вn(А).

Пример. 5.1.24. Для приема зачета преподаватель заготовил 50 задач: 20 задач по теории вероятностей, 30 – по математической статистике. Для сдачи зачета студент должен решить первую же доставшуюся ему наугад задачу. Какова вероятность того, что студент сдаст зачет, если он умеет решать 18 задач по теории вероятностей и 15 задач по математической статистике?

○Вероятность получить задачу по теории вероятностей (событие В₁) равна Р(В₁)=20/50=0,4, по математической статистике (событие В₂) – Р(В₂)=30/50=0,6. Если событие А состоит в том, что задача решена, то Р_В1(А)=18/20=0,9, Р_В2(А)=15/30=0,5. Тогда, используя формулу полной вероятности, получим

Р(А)=0,4·0,9+0,6·0,5=0,36+0,3=0,66.●

Формула Байеса

Пусть событие А может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … В_n, которые образуют полную группу событий. Если событие А уже произошло, то вероятности событий могут быть переоценены по формуле Байеса:

(5.1.13)

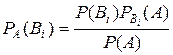
Пример 5.1.25. Для приема зачета преподаватель заготовил 50 задач: 20 задач по теории вероятностей, 30 – по математической статистике. Для сдачи зачета студент должен решить первую же доставшуюся ему наугад задачу. Студент умеет решать 18 задач по теории вероятностей и 15 задач по математической статистике. Известно, что студент сдал зачет. Какова вероятность того, что студенту досталась задача по теории вероятностей.

○В примере 1.2.24. найдено, что вероятность получить задачу по теории вероятностей (событие В₁) равна Р(В₁)=0,4, по математической статистике (событие В₂) – Р(В₂)=0,6, 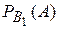=0,9, Р(А)=0,66, где А состоит в том, что задача решена. Тогда вероятность того, что студенту досталась задача по теории вероятностей

●

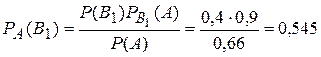Формула Бернулли

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0<p<1), событие наступит ровно k раз (безразлично в какой последовательности), равна

(5.1.14)

,

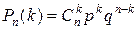где q – вероятность ненаступления события, т.е. вероятность противоположного события.

Пример 5.1.25. На экзамене 20 билетов. Какова вероятность вытянуть один и тот же билет для 3 студентов, если экзаменатор тут же кладет вытянутый билет обратно?

○ .●

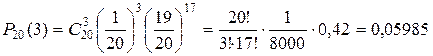Вероятность того, что в n независимых испытаниях

а) событие наступит менее k раз: ;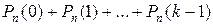

б) событие наступит более k раз: ;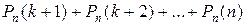

в) не менее k раз: ;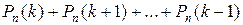

г) не более k раз: .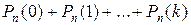

Формула Пуассона

Предположим, что мы хотим вычислить вероятность 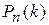появления события А при большом числе испытаний n, например, 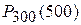. В этом случае непосредственное вычисление по формуле Бернулли значительно усложняется, тем более, если учесть, что р может быть очень малым, например

.

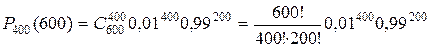Конечно, расчеты могут быть произведены с помощью компьютера, например, с использованием MS Excel. Однако, существует более простая приближенная формула – формула Пуассона.

Если вероятность р постоянна и мала, число испытаний п велико и число l= пр – незначительно (будем полагать, что l= пр£10), то вероятность 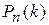того, что событие А появится k раз в п независимых испытаниях можно приближенно (тем точнее, чем больше п) найти по формуле Пуассона:

(5.1.15)

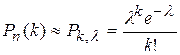
В приложении 3 приведены значения функции Пуассона .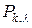

Пример 5.1.26. На факультете учится 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?

○Вероятность того, что день рождения студента 1 сентября, равна р=1/365. Так как р=1/365 – мала, n=1825 – велико и l=пр=1825·(1/365)=5£10, то применяем формулу Пуассона (5.1.15.):

Р₄(5)»Р_4,5=0,1755 (по приложению 3)●

Конспект 1. Элементы теории вероятностей

Основные понятия теории вероятностей