Постановка граничных условий

Граничные условия для системы уравнений движения жидкости будем определять из физических соображений. Для идеальной жидкости принято считать, что отсутствуют не только силы трения между частицами, но и между частицами жидкости и стенкой. Это приводит к необходимости в качестве граничных условий принять так называемый режим скольжения, при котором на границе не накладывается никаких ограничений на касательную составляющую скорости v_τ, а нормальная составляющая скорости v_n, если стенка является непроницаемой, должна равняться нормальной составляющей скорости стенки в этой точке. Если стенка недеформируемая и покоится, то на всей границе v_n = 0.

Для вязкой жидкости принято считать, что силы трения, которые существуют между частицами жидкости, при взаимодействии с материалом стенки приводят к их сцеплению. Это явление называют режимом прилипания. В этом случае выставляется требование равенства нулю касательной составляющей скорости v_τ = 0. Что же касается требования к нормальной составляющей скорости, то оно остается таким же, как и при режиме скольжения.

Следует отметить, что режим прилипания реализуется для многих видов материалов стенки, однако не является абсолютным. Существует целый ряд материалов, для которых условие прилипания не выполняется. Это свойственно, в частности, некоторым полимерам, пористым материалам, кровеносным сосудам и т.д. В этих случаях принимают режим частичного проскальзывания. К этому режиму прибегают и в том случае, когда вблизи стенки существует тонкий слой, в котором уравнения гидродинамики будут некорректны, и граничные условия ставятся не на стенке, а с внутренней стороны пограничного слоя. Для простейшего случая одномерного течения это граничное условие имеет вид

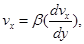(19)

где β - коэффициент проскальзывания, который имеет размерность длины и поэтому его ещё называют длиной проскальзывания. Этот коэффициент определяется экспериментально.

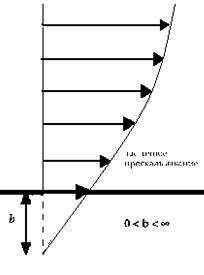Для наглядности на рис. 38 приведен профиль скорости для одномерного течения в случае частичного проскальзывания.

Помимо граничных условий на стенке, которые выбираются исходя из физических соображений, граничные условия ставятся и на воображаемой поверхности, ограничивающей рассматриваемый в задаче объем жидкости. Это может быть, например, начальная и конечная границы рассматриваемого участка трубы. В этом случае задаются значения скорости и (или) давления на заданной границе.

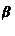
Встречаются задачи, в которых нужно поставить граничные условия на свободной поверхности. Для вязкой жидкости в этом случае напряжение на этой поверхности должно быть равно нулю, т.е.

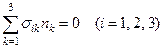, (20)

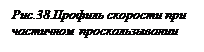где n_k (k=1, 2, 3) – направляющие косинусы нормали к свободной поверхности

Уравнения газодинамики

Как мы уже отмечали в предыдущей главе, уравнения газовой динамики отличаются от уравнений гидродинамики за счет того, что плотность не является постоянной величиной. По этой причине уравнения газодинамики описывают движение не только собственно газов, но и жидкости, если она в какой-то задаче проявляет свойства сжимаемости.

Эффект изменения плотности в газах тоже наблюдается и учитывается не во всех задачах. Он становится заметным и учитывается в задачах, характеризующихся большими скоростями и градиентами давлений, таких как полет высокоскоростных самолетов и ракет, распространение взрывных волн и т.п. При этом эффекты вязкости практически не проявляются.

Мы рассмотрим для простоты одномерное движение газа в отсутствии внешних сил и источников. В этом случае уравнение неразрывности с учетом изменения плотности будет иметь вид

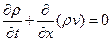(21)

Уравнение движения при сделанных предположениях становится скалярным

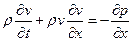(22)

Неизвестными величинами являются, как и раньше, давление – p и скорость – v, а теперь еще и плотность – ρ. В связи с появлением новой неизвестной функции нам необходимо иметь еще одно уравнение. Однако, такое уравнение можно записать, только определившись со свойствами газа.

Если ограничиться рассмотрением идеального газа, т.е. газа в котором взаимодействие между молекулами отсутствует, или точнее говоря, достаточно мало, то можно для него записать известное уравнение состояния

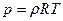(23)

Однако, это уравнение, как мы видим, содержит еще и температуру, которая известна и остается постоянной только для изотермических процессов. Можно избавиться от температуры в нужном нам уравнении и в случае адиабатического процесса, т.е. происходящего без теплообмена с внешней средой. При адиабатическом процессе движения газа энтропия каждой его частицы остается постоянной, а тогда её полная производная равна нулю

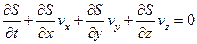
Это уравнение выражает адиабатичность движения идеального газа. В частном случае, если в какой-то момент энтропия окажется одинаковой во всех точках газа, то она останется одинаковой и во все последующие моменты времени. В этом случае уравнение адиабатичности сведется к равенству энтропии постоянной величине

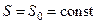
Такое движение газа называется изэнтропическим. При этом уравнение состояния принимает вид

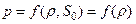(24)

Конкретным видом этой зависимости является адиабата Пуассона

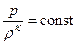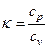, где (24')

Здесь c_p – теплоемкость при постоянном давлении, а c_v – теплоемкость при постоянном объеме, которые считаются постоянными.

В общем случае можно записать уравнение состояния следующим образом

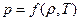(25)

Следует заметить, что и уравнение (23) и уравнение (24) или (25), каждое из которых замыкает систему уравнений газодинамики, не является дифференциальным.

Полученные уравнения газодинамики (21), (22) и (25) можно также считать уравнениями движения идеальной сжимаемой жидкости в отсутствии внешних сил.

Закон сохранения энергии

Воспользовавшись уравнениями (21) и (22) мы можем получить закон сохранения энергии для идеального газа. Рассмотрим энергию единицы объема. Она равна

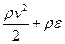, (26)

В этом выражении первый член представляет кинетическую энергию, а второй – внутреннюю энергию, где ε – внутренняя энергия единицы массы. Для идеального газа она равна ε = с_vT, где с_v , как уже говорилось, есть теплоемкость при постоянном объеме. Запишем теперь изменение энергии в единицу времени

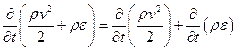(27)

Произведя операцию дифференцирования в первом слагаемом левой части этого уравнения, мы затем воспользуемся уравнениями (21) и (22). В результате получим

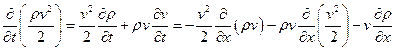(28)

Для преобразования второго слагаемого в правой части воспользуемся записью первого начала термодинамики, выражающего закон сохранения энергии в терминах теплоты и работы

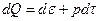(29)

где dQ – количество тепла, получаемое объектом извне, а pdτ – работа, необходимая для изменения удельного объема τ =1/ρ на величину dτ.

Если процесс адиабатический, то dQ = 0 и тогда

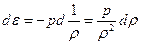(30)

Пользуясь этим равенством, можем записать

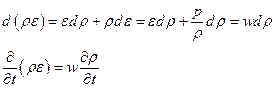(31)

где w – так называемая тепловая функция или теплосодержание единицы массы.

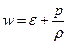(32)

Далее можно убедиться, что в силу соотношений (30) и (32) производная 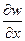удовлетворяет уравнению

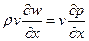(33)

Учитывая, наконец, уравнение (22) и выражения (27), (28), (31) и (33) мы получим закон сохранения энергии в дифференциальной форме

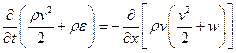(34)

Физический смысл этого равенства легко понять, если проинтегрировать его некоторому объему (в нашем, одномерном, случае по отрезку (x₁, x₂)

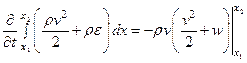(35)

В левой части равенства стоит изменение энергии в единицу времени на интервале (x₁, x₂), а в правой части записан поток энергии, вытекающей в единицу времени из рассматриваемого объема.

В заключении отметим, что если эффектом теплопроводности пренебречь нельзя, то в правой части уравнения сохранения энергии (34), в квадратных скобках появится дополнительный член, описывающий поток тепла, а именно

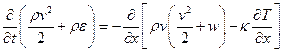, (36)

где κ – коэффициент теплопроводности.

Таким образом, мы получили еще одно уравнение в частных производных, которое связывает неизвестные функции v, p, ρ и T и позволяет замкнуть систему уравнений (22), (23) и (26).