Разрыв потенциала двойного слоя

Рассмотрим сначала случай двух независимых переменных. Согласно определению потенциал двойного слоя в этом случае выражается интегралом

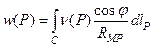
Рассмотрим некоторый элемент дугиdl, концами которого являются точки Р и Р₁. проведем через точку Р дугу окружности радиуса МРс центром в точке М до пересечения с отрезком МР₁ в точке Q (Рис. 34), тогда с точностью до бесконечно малых высшего порядка можно написать

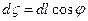и ,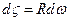

где 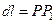, , 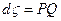dω – угол, под которым видна дуга dl из точки М. Знак dω совпадает со знаком сosφ. Если 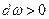, т.е. 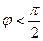, то из точки М видна «внутренняя» сторона кривой С ; при 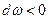( 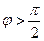) из точки М видна «наружная» сторона этой кривой. Отсюда следует, что угол видимости некоторой дуги Р₁Р₂ равен углу Р₁МР₂, который описывает луч МР, когда точка Р пробегает дугу Р₁Р₂.

Рассмотрим потенциал двойного слоя W ⁰ на замкнутой кривой C с постоянной плотностью 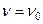. Луч МР описывает угол

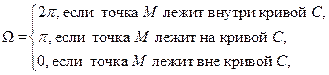
когда точка Р пробегает всю кривую С. Отсюда для потенциала W ⁰ пролучаем

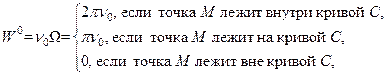
Таким образом, потенциал двойного слоя с постоянной плотностью является кусочно-постоянной функцией, причем

,

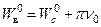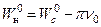, (14)

где W_в⁰, W_с⁰, W_н⁰ – значение потенциала внутри, на и вне кривой С.

Проводя аналогичные рассуждения для случая трех независимых переменных, мы придем к формуле

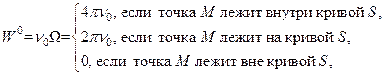
Характеризующей кусочное постоянство функции W ⁰, а также к формулам

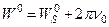
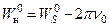(15)

где W_в⁰ и W_н⁰ – значения потенциала W ⁰ внутри и снаружи поверхности S, а W_S⁰ – значение W ⁰ на поверхности S.

Рассмотрим теперь потенциал двойного слоя с переменной плотностью и докажем, что в точках непрерывности плотности имеют место формулы, аналогичные формулам (14) и (15).

Пусть Р₀ – точка поверхности S, в которой функция ν(Р) непрерывна. Рассмотрим функцию

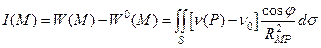
Докажем, что функция I непрерывна в точке Р₀. Для этого достаточно доказать равномерную сходимость интеграла I(М) в точке Р₀. Зададим некоторое 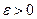. Из непрерывности функции ν(Р) в точке Р₀ следует, что для любого наперед заданного числа 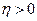можно найти S₁ – окрестность точки Р₀ на поверхности S – такую, что

,

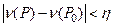если 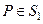. Представим интеграл I в виде суммы

,

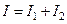где интеграл I₁ берется по поверхности S₁, а I₂ – по поверхности S₂ = S – S₁. Из определения S₁ следует, что

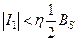
где В_S – постоянная, определяемая условием

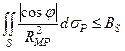(16)

при всевозможных положениях точки М, не зависящих от выбора поверхности S₁.

Выбирая 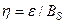, мы убеждаемся в том, что для любого 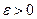можно найти такое S₁, содержащее Р₀, что

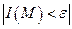
при любом положении точки М. Отсюда и следует равномерная сходимость интеграла I(М) в точке Р₀, а также его непрерывность в этой точке.

Если W_в⁰ и W_н⁰ – пределы потенциала W(M) при 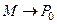с внутренней и наружной сторон поверхности S, то

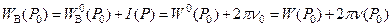
и аналогично

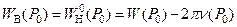
Таким образом, справедливость формулы (15) установлена.

Проведенное выше доказательство справедливо для поверхностей, удовлетворяющих условию ограниченности (16). Для выпуклой поверхности, которую всякий луч из точки М пересекает не более двух раз, 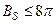; для поверхностей, состоящих из конечного числа выпуклых частей, В_S также ограничено. Таким образом, наше доказательство относится к весьма широкому классу поверхностей.

Все проведенные выше рассуждения остаются в силе и для функций двух независимых переменных. В этом случае формулы (14) принимают вид

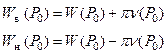(17)