Потенциалы простого и двойного слоя

Рассмотрим поле, создаваемое массами (зарядами), непрерывно распределенными по поверхности S с поверхностной плотностью μ(Р)в некотором слое и определим потенциал поля, создаваемого этим слоем в некоторой точке M за его пределами. При этом толщина слоя должна быть много меньше расстояния до точки M. Тогда искомый потенциал будет представляться поверхностным интегралом

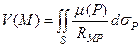, (9)

который называется потенциалом простого слоя.

Теперь рассмотрим диполь, образованный массами – m и+m (или зарядами – q и+q), расположенными в точках Р₁ и Р₂ на малом расстоянии Δl. Произведение mΔl=N называется моментом диполя. Тогда потенциал этого диполя в точке в некоторой точке М равен

,

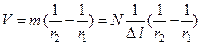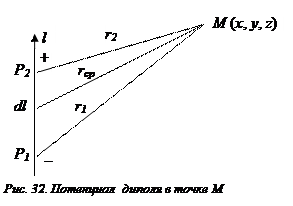Где r₁ и r₂ – расстояния от точек Р₁ и Р₂ до точки М (Рис. 32).

Если Δl мало по сравнению с расстоянием до точки М , то можно написать

,

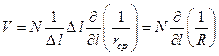где R – расстояние от точки М(x, y, z) до некоторой средней точки между Р₁ и Р₂. Производная по направлению l будет равна

,

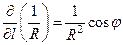где φ – угол между R и l. Таким образом, потенциал диполя равен

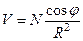(10)

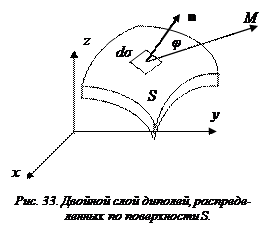
Рассмотрим теперь поверхность S (Рис. 33), по которой равномерно распределены диполи таким образом, что по одну сторону поверхности будут распределена отрицательная масса (заряд), по другую, на расстоянии δ – положительная масса (заряд). Обозначим через n нормаль к поверхности, направленную от отталкивающей массы к притягивающей, т.е. совпадает с направлением l. Переходя к пределу при δ, стремящемся к нулю, получим распределенный по поверхности двойной слой. Если ν(Р) – поверхностная плотность диполя, то дипольный момент элемента поверхности dσ_P будет равен

,

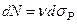а для потенциала элемента dσ_P в точке M(x, y, z) мы будем иметь

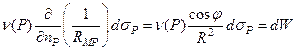
Тогда потенциал, создаваемый всей поверхностью, будет равен

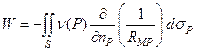(11)

Этот потенциал называется потенциалом двойного слоя.

Потенциалы простого и двойного слоя в случае двух независимых переменных имеют вид

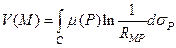, (12)

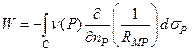, (13)

где С – некоторая кривая на плоскости x, y; μ – линейная плотность простого слоя; ν – линейная плотность дипольного момента двойного слоя.

Поверхности Ляпунова

Потенциалы простого и двойного слоя в точках поверхности S являются несобственными интегралами. Покажем, что эти интегралы сходятся для определенного класса поверхностей, называемых поверхностями Ляпунова, если плотность в каждом из них ограничена.

Поверхность называется поверхностью Ляпунова, если выполнены следующие условия:

а) в каждой точке поверхности S существует единственная нормаль;

б) существует такое число d > 0, что прямые, параллельные нормали в какой-либо точке Р поверхности S, пересекают не более одного раза часть поверхности S, лежащую внутри сферы радиуса d с центром в точке Р. Эти участки поверхности называются окрестностями Ляпунова.

в) угол между нормалями в двух произвольных точках поверхности Р' и Р'' не превосходит величины 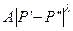, где 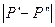– расстояние между этими точками, А и λ – постоянные числа, причем .

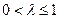Можно доказать, что в точках, лежащих на поверхности S, потенциал двойного слоя

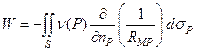
является сходящимся несобственным интегралом, если S – поверхность Ляпунова.

Можно также установить, для поверхностей Ляпунова потенциал простого слоя

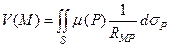
также сходится в точках поверхности. Следует, правда, отметить, что эта сходимость имеет место и для поверхностей более широкого класса.