Задача о распространении тепла в изотропном твердом теле.

Рассмотрим твердое тело, температура которого в точке (x,y,z)в момент времени t определяется функцией u(x, y, z, t).

Как и в случае однородного стержня, нам потребуется знание плотности материала ρ, удельной теплоемкости с и теплопроводности материала k, которые мы будем считать постоянными.

Для вывода уравнен функцией температурного влияния мгновенного точечного источника тепла ия распространения тепла выделим внутри тела произвольный объем V, ограниченный гладкой поверхностью S, и рассмотрим изменение количества тепла в этом объеме за промежуток времени Δt.

Сначала определим количества тепла, необходимого для изменения температуры элемента объема Δτза время 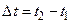на величину :

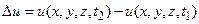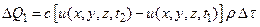
Тогда количество тепла, необходимое для изменение температуры всего тела на ту же величину, будет равно

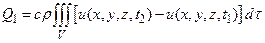
но поскольку

,

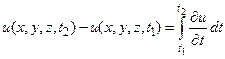то в результате получим

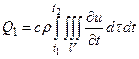(28)

Теперь запишем количества тепла, поступающего внутрь объема за промежуток времени Δt через поверхность S:

,

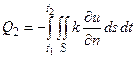где n – внутренняя нормаль к поверхности S. В результате применения формулы Гаусса-Остроградского к записанному интегралу получим

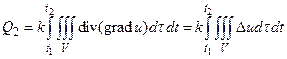(28)

Посчитаем также количества тепла, произведенного за тот же промежуток времени внутренними источниками тепла, непрерывно распределенных по объему V с плотностью f(x,y,z,t). Оно будет равно

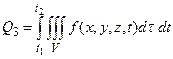(29)

Исходя из условия баланса, можно записать, что 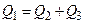. Согласно этому условию мы получим

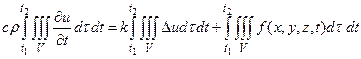
Так как подынтегральная функция непрерывна, а объем V и промежуток времениΔt произвольны, то можем записать

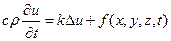
или, вводя величины 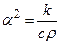и 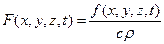, окончательно будем иметь

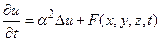(30)

Это и есть уравнение теплопроводности однородного изотропного тела, которое представляет собой уравнение Пуассона в пространстве.

В отсутствии источников тепла оно переходит в уравнение Лапласа

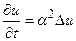(31)

Для полной постановки задачи нужно сформулировать начальное условие и граничные условия.

В начальный момент времени задается распределение температуры по рассматриваемому объему в начальный момент времени, а именно

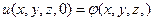(32)

Граничное условие, как и раньше, может быть задано тремя основными способами:

1) в каждой точке ограничивающей поверхности S задается температура

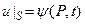, (33)

где P – текущая точка на поверхности S;

2) на поверхности S задается тепловой поток

,

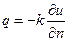откуда можно записать

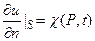(34)

3) на поверхности S происходит теплообмен с окружающей средой, температура которого известна и может быть функцией времени T(t). Тогда по закону Ньютона о теплообмене

,

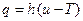где h – коэффициент теплообмена, который мы будем считать постоянным.

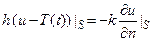
или, положив 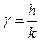, окончательно получим

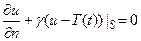(35)

Уравнение диффузии

Если среда неравномерно заполнена газом, то имеет место диффузия его из мест с более высокой концентрацией в места с меньшей концентрацией. Сходное явление имеет место и в растворах, если концентрация растворенного вещества в среде не постоянна.

Рассмотрим процесс диффузии в полой трубке или в непроницаемой трубке, заполненной пористой средой. При этом мы будем предполагать поперечное сечение трубки S настолько малым, что концентрацию газа или раствора в поперечном сечении можно считать постоянной. Будем также считать, что источники вещества в трубке отсутствуют. Процесс диффузии может быть описан функцией u(x,t), представляющей концентрацию в сечении x в момент времени t.

Согласно закону Нерста масса газа, протекающая через сечение x за промежуток времени (t, t +Δt) равна

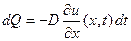, (36)

где D – коэффициент диффузии.

Исходя из определения концентрации, изменение массы газа на участке трубки (x₁,x₂) при изменении концентрации на величину Δu равно

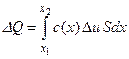, (37)

где c(x) – коэффициент пористости среды, который есть отношение суммарного объема пор к полному объему, в нашем случае равному Sdx.

Теперь составим уравнение баланса массы газа на участке (x₁,x₂) за промежуток времени (t₁, t₂):

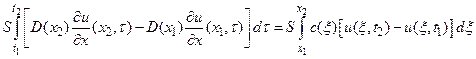
Откуда, также как и в предыдущем параграфе, получим

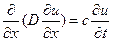, (38)

которое и является одномерным уравнением диффузии.

Если коэффициент диффузии постоянен, то с учетом обозначения 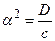уравнение диффузии приобретает вид

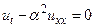, (39)

который аналогичен одномерному уравнению теплопроводности в отсутствии источников тепла.