Для одномерного волнового уравнения

При решении граничных задач следует убедиться в существовании решения и его единственности. Существование решения либо устанавливается в процессе изложения метода решения, либо доказывается теорема существования. Единственность устанавливается доказательством соответствующей теоремы единственности.

В настоящем параграфе приводится доказательство теоремы единственности для одномерного волнового уравнения достаточно общего вида при заданных начальных условиях и граничных условиях первого, второго и третьего рода. Эта теорема формулируется следующим образом.

Существует только одна функция u(x, t), определенная в области 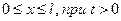, которая удовлетворяет уравнению

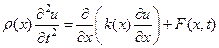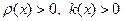, ( ) (112)

а также начальным и граничным условиям

(113)

(114)

если выполнены следующие условия:

1) функция u(x, t) вместе со своими первыми и вторыми производными непрерывна на отрезке ,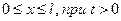

2) коэффициенты ρ (x) и k (x) непрерывны на отрезке .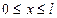

Допустим, что существует два решения рассматриваемой задач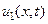и:

и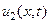

Рассмотрим разность

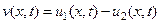
Функция 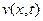, очевидно, удовлетворяет однородному уравнению

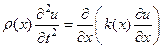(115)

и однородным начальным и граничным условиям

(116)

(117)

а также условию 1) теоремы.

Докажем что функция 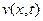тождественно равна нулю. Для этого рассмотрим функцию

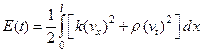(118)

и покажем, что она не зависит от t. В задаче о колебании струны эта функция представляет собой полную энергию струны в момент времени t. Продифференцировав E(t) по t получим

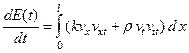
Интегрируя первое слагаемое по частям, получим

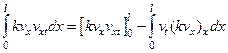(119)

В силу условий (116) и (117) первое слагаемое правой части равно нулю, следовательно

,

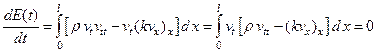т.е. 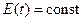. Тогда учитывая начальные условия, получаем

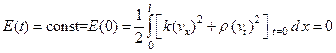(120)

а тогда и формула (118) принимает вид:

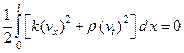
откуда, учитывая положительность ρ (x) и k (x), заключаем, что

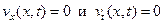(121)

Это, в свою очередь, означает, что

,

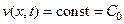но, в соответствии с начальными условиями

,

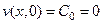А тем самым доказано, что 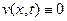. Следовательно, если существуют две функци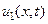и и 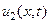, удовлетворяющие всем условиям теоремы, то

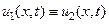(122)

Единственность решения задачи с граничными условиями второго рода доказывается аналогично. Введенная в рассмотрение функция 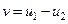в этой задаче будет удовлетворять граничным условиям

, (123)

выполнение которых также приведет к обращению в нуль первого слагаемого в формуле (119). Дальнейшее доказательство проводится также как и для первой краевой задачи.

Для третьей краевой задачи также рассматриваются два решения u₁ и u₂. Тогда для функции 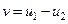граничные условия будут однородными:

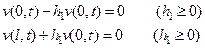(124)

Теперь представим первое слагаемое в формуле в виде

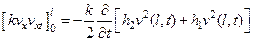
и проинтегрируем 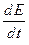в пределах от 0 до t. В результате получим

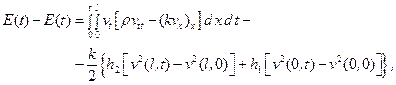
откуда в силу уравнения для v и граничных условий следует, что

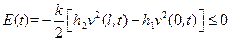, (125)

но в силу неотрицательности подынтегральной функции E(t) должно быть больше или равно нулю. Из чего следует, что 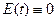, а следовательно и

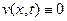(126)

Тем самым единственность третьей краевой задачи доказана.

Г л а в а III. Двумерные и трехмерные задачи для волнового уравнения

В двумерном и трехмерном случаях волновое уравнение можно записать следующим образом

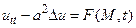, (1)

где М – точка на плоскости или в пространстве. Двумерное волновое уравнение обычно связывают с задачей о колебании мембраны. К трехмерному волновому уравнению приводятся задачи о течении жидкости, скорость которой имеет потенциал, о распространения звука в газе, о распространении электромагнитных полей в непроводящей среде и задачи теории упругости. Эти задачи мы рассмотрим в последующих главах.

Во всех этих задачах волновое уравнение описывает процесс распространения волн. В одномерном случае мы в этом убедились при рассмотрении формулы Даламбера. Такие волны называют плоскими волнами. Однако и в трехмерном пространстве в случае сферической симметрии мы будем иметь дело с распространением звуковых или электромагнитных волн, которые на большом расстоянии от источника можно считать плоскими. Двумерные волны называются цилиндрическими волнами, а трехмерные – сферическими волнами.

Выведенную нами ранее формулу Даламбера можно обобщить соответствующим образом на двухмерный и трехмерный случаи. Начнем с трехмерного случая.