Предмет математической физики.

Математическая физика это раздел высшей математики, в котором физические процессы описываются дифференциальными уравнениями в частных производных, а также интегральными уравнениями.

Математическая физика формировалась в результате необходимости решать задачи физики, формулировка которых была невозможна без использования уравнений в частных производных, то есть уравнений, в которые входят неизвестная функция и её частные производные.

Само обращение к частным производным было обусловлено тем, что величины, описывающие состояние объекта исследования и процессы в нём происходящие, как правило, являются функциями нескольких переменных. (С другой стороны) В то же время, большинство физических законов было сформулировано для физических величин, характеризующих тело в целом (масса, объём, площадь поверхности, температура, теплоёмкость и т.д.). Эти величины связывались между собой определёнными соотношениями и могли меняться во времени. Однако изменения физических величин при переходе от одной точки тела к другой не рассматривались. Это видно, в частности, на примерах задач механики, в которых от понятий материальной точки и абсолютного тела необходимо было перейти к новому физическому понятию – деформируемые тела и среды, которые включают в себя твёрдые деформируемые тела, жидкие и газообразные среды. По существу нужно было законы механики, сформулированные для тела в целом, записать для каждой точки этого тела, используя функции, зависящие от пространственных координат каждой точки и времени. Примером могут служить уравнения движения идеальной сжимаемой жидкости, впервые представленные Л. Эйлером в 1755 г.

Аналогичная ситуация сложилась, когда нужно было получить уравнения для описания процессов теплопроводности и распределения тепла, в которых нужно было прейти от понятия температура тела к понятию температуры в каждой точке тела. Со временем перечень таких явлений расширялся. Появились уравнения в частных производных для описания процессов в электростатическом поле, процессов диффузии и т.д.

Однако некоторые физические законы, такие как законы электромагнитного поля, впервые опубликованные Максвеллом в 1873 г. в его «Трактате об электричестве и магнетизме, с самого начала формулировались на языке уравнений в частных производных, точнее говоря, систем таких уравнений.

В целом, те или иные уравнения в частных производных нужно рассматривать как математические модели физических процессов или состояний среды (в стационарном случае), в которых величины, характеризующие этот процесс или состояние, являются функциями нескольких переменных. При этом следует иметь в виду, что каждое уравнение получено при определенных допущениях и предположениях, которые позволяют идеализировать некоторые свойства объекта или процесса и пренебречь другими. Строго говоря, уравнения колебания струны, стержня, мембраны, надо бы называть уравнения колебания модели струны, модели стержня и модели мембраны, и хотя слово модель каждый раз не упоминается, оно, тем не менее, каждый раз подразумевается.

Следует также отметить, что для некоторых уравнений в частных производных оказывалось целесообразным свести их к интегральным уравнениям, то есть к уравнениям, в которых неизвестная функция входит под знак интеграла.

Со временем оказалось, что к уравнениям с частными производными приходится обращаться не только при записи физических законов, но и законов, сформулированных для других областей знания: экономики, социологии, физиологии и т.д. При этом методы решения уравнений с частными производными не зависели от природы описываемого процесса или состояния. Это привело к формированию раздела математики под названием теория дифференциальных уравнений в частных производных, а математическая физика стала разделом высшей математики. Однако смешивать эти два понятия не следует, тем более что в математической физике, как уже отмечалось, используются и интегральные уравнения, методы решения которых составляют раздел высшей математики под названием теория интегральных уравнений. Далее мы будем иметь дело толь с уравнениями математической физики, дифференциальными или интегральными.

Предлагаемый учебник частично возвращает читателя к первоосновам математической физики, имея в виду необходимость подготовить специалистов, умеющих не только знать, как выводить и решать известные уравнения, но и осуществлять математическую постановку новых физических задач, что особенно важно для студентов направления «Прикладные математика и физика».

С этой целью в предлагаемом курсе лекций особое внимание уделяется физической основе уравнений в частных производных, которые можно рассматривать как средство математического моделирования физических процессов, а также физическому смыслу начальных и граничных условий. Такие разделы математической физики как специальные функции, теория интегральных уравнений и некоторые численные методы решения уравнений математической физики отнесены к дополнительным главам к основному курсу и напечатаны отдельно.

Основные понятия и определения.

Для уравнений математической физики независимыми переменными обычно являются координаты x, y, z (или другие пространственные координаты) и время t. Именно для этих независимых переменных мы и сформулируем основные определения.

Уравнение, связывающее независимые переменные x, y, z и t, неизвестную функцию u (x, y, z, t) и частные производные от неизвестной функции, называется дифференциальным уравнением в частных производных.

Оно имеет вид

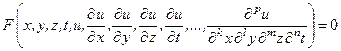, (1)

где p = 1, 2, …, N , а .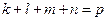

При записи уравнений с частными производными используется также более компактная форма записи частных производных, а именно

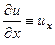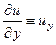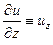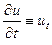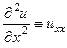, , , , и т.д.

Порядок старшей производной, входящей в уравнение вида (1), называется порядком уравнения в частных производных.

Уравнение называется линейным относительно старших производных, если старшие производные входят в уравнение только в первой степени, а коэффициенты при этих производных являются функциями только независимых переменных.

Если же указанные коэффициенты зависят также и от неизвестной функции и её производных более низкого порядка, то такое уравнение называется квазилинейным.

Уравнение называется линейным, если оно линейно относительно неизвестной функции и всех его производных, а коэффициенты являются функциями только независимых переменных. В качестве примера приведем вид линейного уравнения второго порядка относительно двух независимых переменных x и y,

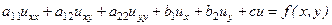, (2)

где коэффициенты a₁₁, a₁₂, a₂₂, b₁, b_2, c зависят только от x и y. В качестве одной из переменной может выступать время t.

Если функция независимых переменных в правой части уравнения равна нулю, то уравнение называется однородным.

Решением уравнения в частных производных называется всякая функция u(x, y, z, t), которая, будучи подставлена вместе со своими частными производными в уравнение, обращает его в тождество.

Каждое уравнение в частных производных имеет бесчисленное множество решений. При решении конкретной физической задачи выбирают то решение, которое вытекает из её физического смысла. Одним из видов таких условий являются начальные условия, относящиеся к моменту времени, с которого начинается изучение данного физического процесса. Для уравнения, содержащего производные по времени порядка n, нужно в начальный момент времени задать саму функцию и её производные до порядка n – 1 включительно, которые будут являться функциями только координат. Если физическая задача формулируется для некоторой ограниченной области, то на границе формулируются граничные условия. Для этого сама функция и (или) её производные (не выше n – 1 порядка, где n – порядок старшей производной по координате) задаются как функции времени.

Путем линейного преобразования независимых переменных уравнение в частных производных можно привести к наиболее простому виду. Так уравнение (2) можно привести к виду, не содержащему смешанного произведения. Наиболее простой вид того или иного уравнения называется каноническим видом этого уравнения. Этот вид может оказаться не единственным.