Принятие решений о браковке методами статистического приемочного контроля.

2.1 Найти объем выборки и приемочный уровень при контроле

продукции по методу Неймана – Пирсона. Решить задачу

различения двух гипотез :

приемка партии,

браковка партии.

Исходные данные:

МПа – математическое ожидание предела прочности,

МПа - среднее квадратическое отклонение предела прочности,

МПа - предел прочности материала по ГОСТу,

- риски поставщика и заказчика.

2.2 Найти объем выборки n и приемочный уровень при контроле надежности по методу Неймана - Пирсона. При решении задачи принять следующие исходные данные:

1).

( ) ( ) ( )

2).

3). .

4) .

Закон распределения нормальный.

2.3.. Найти области приемки ( браковки ) при статистическом контроле надежности методом последовательного анализа. При проведении расчета принять следующие исходные данные:

.

Закон распределения коэффициента запаса принять нормальным. ( )

2.4. Оценить средний объем испытаний n при контроле надежности по методу Вальда (последовательного анализа) при нормальном законе распределения контролируемого параметра. При проведении расчетов принять следующие исходные данные:

.

Основные расчетные соотношения

Этапы проверки статистических гипотез по методу Неймана- Пирсона:

1) определение гипотез и ;

2) выбор статистики и задание уровня значимости ;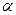

3) определение по таблицам, по уровню значимости 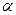и по альтернативной гипотезе критической области;

4) вычисление по выборке значения статистики;

5) сравнение значений статистики с критической областью;

6) принятие решения: если значение статистики не входит в критическую область, то принимается гипотеза и отвергается гипотеза , а если входит в критическую область, то отвергается гипотеза и принимается гипотеза .

7) приемочный уровень и число испытаний определяются из решения системы:

В дальнейшем предположим, что случайная величина Х распределена нормально.

Ставится задача различения двух гипотез о значении математического ожидания:

Для заданного риска поставщика , имеем

;

где 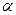-- приемочный уровень, -- точечная оценка математического ожидания.

Отсюда

;

где -- объем выборки, -- среднее квадратическое отклонение.

Приравнивая аргументы, получим

.

Принимая риск заказчика ,равным ,найдем

;

Отсюда

;

Приравнивая аргументы, получим

.

Вычитая из первопго равенства второе, найдем

Отсюда

Из первого соотношения имеем

Отсюда .

Задача выборочного контроля в данном случае состоит в том, чтобы по результатам анализа выборочных характеристик (среднего арифметического значения ) сделать заключение о браковке или приемки партии.

В дальнейшем рассмотрим схему проведения количественного контроля. Предположим, что партия забраковывается, когда процент брака равен и принимается когда процент брака равен .

Таким образом требуется различить две гипотезы:

гипотеза приемка партии;

гипотеза браковка партии.

От исходных гипотез перейдем к гипотезам различения математических ожиданий:

; .

При решении задачи предположим, что отказ наступает при выполнении условия .

Тогда, в предположении нормального закона распределения, вероятность отказа будет равна

,

где аргумент функции нормированного нормального распределения, соответствующий вероятности отказа . Приравнивая аргументы, получим

Отсюда найдем .

Для определения приемочного уровня и числа испытаний n воспользуемся соотношениями ,полученными выше. Учитывая, что , получим

,

где ; .

Метод последовательного анализа (метод Вальда)

Согласно критерию отношения вероятностей Вальда, последовательное решающее правило состоит в следующем. Строится отношение правдоподобия:

Отметим, что - это условная плотность вероятности для наблюдаемых значений при истинности гипотезы ( ).

В дальнейшем величина сравнивается с постоянными порогом А и В. Если , то принимается гипотеза ; если , то принимается гипотеза , если , то делается еще одно наблюдение (выбор продолжается). После логарифмирования критическое неравенство примет вид

Рассмотренный критерий называется последовательным критерием отношения вероятностей. Очевидно, последовательный критерий отношения вероятностей обладает определенными оптимальными свойствами, так как он использует всю имеющуюся в распоряжении информацию, включая порядок появления выборочных значений.

Теперь определим значения порогов А и В. Рассмотрим выборку, для которой лежит между А и В для первых испытаний, так что принимаем (отвергаем ). Вероятность получения такой выборки по крайней мере в А раз больше при гипотезе , чем при гипотезе . Учитывая, что вероятность принятия , когда выполняется , равна 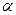, а вероятность принятия , когда выполняется , равна , можно записать;

, где 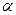- риск поставщика; - риск заказчика.

Отсюда

Аналогично, рассматривая случаи, когда принимается , получим

На практике более удобным является вычисление логарифма отношения правдоподобия, чем непосредственное вычисление отношения правдоподобия.

Тогда неравенства примут вид

- условие продолжения испытаний,

- условие браковки,

- условие приемки.

В дальнейшем рассмотрим построение областей отработки для нормального закона распределения параметров работоспособности системы.

Подставляя в критерий отношения правдоподобия выражения для нормального закона распределения, получим

Записывая условие приемки получим

;

.

Соответственно для условия браковки имеем

;

.

Области принятия решений представлены на рис. 6.2

Рис. 6.2 Области принятия решений.