Таким образом, окончательно получим

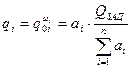
При этом кратность резерва рассчитывается по соотношению

,

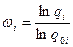В заключение решим задачу нормирования при известной аппроксимационной зависимости

,

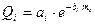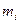где коэффициенты аппроксимации; -- масса i-ой системы.

В этом случае целевая функция будет равна 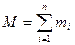.Соответственно для дисциплинирующего условия имеем .

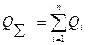Функция Лагранжа примет вид

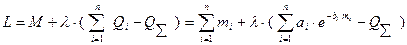
Условие оптимальности можно представить в виде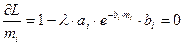

Разрешая систему алгебраических уравнений, для оптимальных уровней вероятности

отказа ,получим

; ; ;

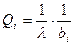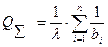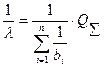Расчет оптимального распределения масс оценивается по соотношениям

; .

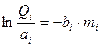Пример выполнения задания №1.1

При «горячем» резервировании кратность резерва оценивается по соотношению

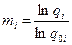, где ,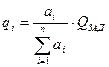

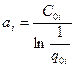
Результаты расчета по программе Matchcad представлены ниже

При написании программы были введены следующие обозначения:

; ;

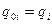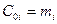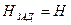
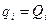
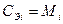
2. Рассчитать коэффициент готовности :

2.1 для резервированной системы с восстановлением отказавших элементов в случае «горячего» резерва. При решении задачи принять : 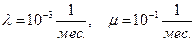. . 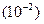Общее число элементов n = 2.

2.2 для резервированной системы с восстановлением отказавших элементов в случае «холодного» резерва. При решении задачи принять : 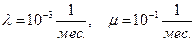. 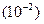Общее число элементов n = 2.

2.3. для резервированной системы с восстановлением отказавших элементов в случае общего резерва. При решении задачи принять : ,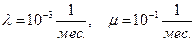

Общее число элементов n = 3 ; число резервных элементов ;

2.4 для резервированной системы с восстановлением отказавших элементов. При проведении расчетов принять 1/мес.; 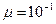1/мес. Количество элементов представлено в таблице.

Общее число элементов N	Число рабочих элементов n	Число ремонтных устройств r

Основные расчетные соотношения

Если число состояний анализируемой системы S конечно и из каждого состояния можно перейти в любое другое, то существуют предельные вероятности состояний, не зависящие от начального состояния системы. Например, система, представленная графом состояний на рис.4.1 , удовлетворяет этим требованиям и, следовательно, приходит со временем к стационарному режиму.

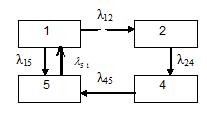
Рис.4.1 Граф состояний системы.

Предельные вероятности состояний дают средние относительные величины времени пребывания системы в данном состоянии. Для вычисления предельных вероятностей состояний нужно составить систему уравнений Колмогорова и положить ее левые части равными нулю. В этом случае система дифференциальных уравнений превратится в систему линейных алгебраических уравнений..

При этом коэффициент готовности оценивается по соотношению

,

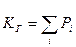где 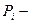вероятность нахождения системы в i-ом состоянии.

Суммирование ведется по всем состояниям ,находясь в которых , система выполняет целевую задачу.

Схема гибели и размножения.

Согласно полученным выше результатам ,имея в расположении размеченный граф состояний, можно легко напасать уравнения Колмогорова для вероятностей состояний, а также написать и решить алгебраические уравнения для финальных вероятностей. Для некоторых случаев удается последние уравнения решить заранее, в буквенном виде. В частности, это удается сделать, если граф состояний системы пред­ставляет собой так называемую «схему гибели и раз­множения» Граф состояний для схемы гибели и размножения имеет вид, показанный на рис.4.2 .

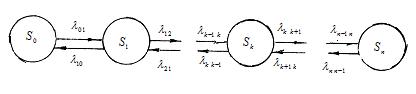
Рис. 4.2 Граф схемы « гибели и размножения ».

Особенность этого графа в том, что все состояния системы можно вытя­нуть в одну цепочку, в которой каждое из средних со­стояний (S₁, S₂, … S_n-1) связано, прямой и обратной стрелкой с каждым из соседних состоянии — правым и левым, а крайние состояния. (S₀, S_n)—только с од­ним соседним состоянием. Термин «схема гибели и раз­множения» ведет, начало от биологических задач, где подобной схемой описывается изменение численности популяции.

Схема гибели и размножения очень часто встреча­ется в разных задачах практики,, поэтому полезно, одни раз и навсегда, найти для нее финальные вероятности состояний.

Предположим, что все потоки событий, переводя­щие систему по стрелкам графа,— простейшие (для краткости будем называть и систему S и протекаю­щий в ней процесс — простейшими).

Пользуясь графом рис.2.11 составим и решим алгебраические уравнения для финальных вероятно­стей состояний (их. существование вытекает из того, что из каждого состояния можно перейти в каждое другое) Для стояния S₀ имеем:

.

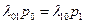Для второго состояния S₁ : .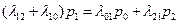

Равенство приводится к виду .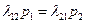

Далее, совершенно аналогично .

и вообще , где к принимает все значения от 0 до n..

Итак, финальные вероятности р₀, р₁,…, р_nудовлетворяют уравнениям

Кроме того, надо учесть нормировочное условие

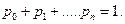
Решим эту систему уравнений из первого уравнения выразим р₁через р₀:

.

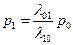Из второго, получим: ,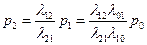

из третьего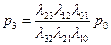

и вообще, для любого k (от 1 до n) .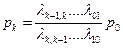

Обратим внимание на то, что в выражении для 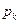в числителе стоит произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо (с начала и до данногo состояния S_k), а в знаменателе — произведение всех интенсивностей стоящих у стрелок, ведущих справа налево (с начала и до S_k )

Таким образом, все вероятности состояний р_0,... р_п выражены черед одну из них (р₀). Подставим эти выражения в нормировочное условие, вынося за скобку р₀

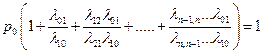
Отсюда получим выражение для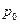

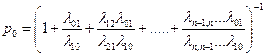
Пример выполнения задания №2.1

Граф состояний имеет вид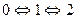

Переходу 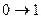соответствует интенсивность 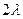, а интенсивность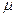

Переходу 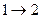соответствует интенсивность 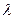, а интенсивность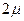

Рассматриваемый случай соответствует схеме «гибели-размножения». Используя правило вычисления вероятности нахождения системы в различных состояниях найдем

; ; .

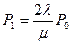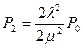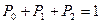После преобразований, получим

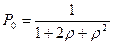, где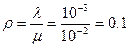

Соответственно коэффициент готовности будет равен

= =

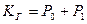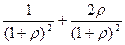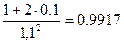
Занятие №5