Рассчитать надежность дублированной системы
1.1 с «теплым» резервированием ( n=2)
1.2 с общим резервированием ( n=4; 
)
1.3 Построить зависимость от времени интенсивностей отказов различных систем:
а) системы с последовательным соединением элементов;
б) «горячего» резерва; в)«холодного» резерва;
г)общего резерва.
При проведении расчетов принять время работы системы t =20 мес. , интенсивность отказа одного элемента системы в рабочем режиме 
. При расчете «теплого» резерва интенсивность отказа неработающего элемента системы принять равной 
.
Основные расчетные соотношения
В случае независимости элементов, вероятность безотказной работы систем с последовательным соединением элементов 
оценивается по соотношению
Соответственно надежность системы с параллельным соединением элементов («горячий» резерв) рассчитывается по формуле
В случае общего резерва расчетное соотношение примет вид
,
где 
надежность i-го элемента.
При оценке надежности систем произвольной структуры, на основе анализа функционирования систем, определяются возможные состояния системы и переходы между ними. По результатам этого анализа строится граф состояний системы. Предположим, что граф состояний имеет вид, представленный на рис. 3.1.
Рис. 3..1 Граф состояний системы.
Каждое состояние системы на графе представлено прямоугольниками. Стрелками отмечены возможные переходы из одного состояния в другое. Каждой стрелке соответствует определенная интенсивность отказа. Допустим, далее, что из анализа функционирования системы определены работоспособные состояния системы, то есть состояния, при нахождении в которых система будет выполнять поставленную перед ней задачу. Тогда надежность будет определяться вероятностью нахождения системы в одном из работоспособных состояний. Если предположить, что для рассматриваемого примера работоспособными являются состояния 1 и 2, то надежность такой системы запишется в виде
Н = Р1 + Р2 ,
где Р1 , Р2 – соответственно вероятности нахождения системы в первом и втором состояниях. Искомые вероятности находятся в результате решения системы дифференциальных уравнений Колмогорова. Число уравнений равно числу всех состояний. Уравнения для каждого состояния составляются по следующему правилу:
слева записывается производная по времени от вероятности нахождения системы в данном состоянии, справа записывается сумма членов, число членов равно числу стрелок, выходящих или входящих в рассматриваемое состояние, каждый член равен произведению интенсивности отказа, стоящей при стрелке, умноженной на вероятность того состояния, из которого исходит стрелка. Знак при слагаемом берется со знаком «+», если стрелка «втекает» в рассматриваемое состояние и со знаком «- », если стрелка «вытекает» из него.
Для графа, представленного на рис.3.1., система дифференциальных уравнений примет вид
Для получения единственного решения необходимо задать пять начальных условий:
, i=1,2,….5.
Так как в каждый момент времени система обязательно находится в одном из рассматриваемых состояний, любое уравнение системы может быть заменено условием нормировки
.
Пример выполнения задания №1.1
Граф переходов имеет вид: 
.
Переход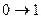 
происходит с интенсивностью 
.
Переход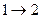 
происходит с интенсивностью 
Составляем уравнения Колмогорова:
; 
.
Применяя преобразование Лапласа к обеим частям уравнений, получим
; 
.
Отсюда
; 
.
Производя обратное преобразование, найдем
; 
.
Таким образом надежность системы будет равна
.
Заметим, что при 
приходим к оценке надежности, соответствующей случаю «холодного» резерва
.
Результаты расчета представлены ниже
Рис. 3. 2 Зависимость надежности, выраженной в белах, от уровня интенсивности отказа x= 