Статистическая гипотеза и общая схема ее проверки

Поскольку статистика как метод исследования имеет дело с данными, в которых интересующие исследователя закономерности искажены различными случайными факторами, большинство статистических вычислений сопровождаются проверкой некоторых предположений или гипотез об источнике этих данных.

Определение 6.2.1. Статистической гипотезой называется любое предположение о виде неизвестного распределения или о параметрах известных распределений.

Пример 6.2.1. Статистическими являются гипотезы:

a. генеральная совокупность распределена по закону Пуассона;

b. дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй – о параметрах двух известных распределений.

Гипотеза «На Марсе есть жизнь» не является статистической, поскольку в ней не идет речь ни о виде, ни о параметрах распределения.

Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине данные гипотезы целесообразно различать.

Определение 6.2.2. Нулевой (основной) называют выдвинутую гипотезу H₀.

Определение 6.2.3. Конкурирующей (альтернативной) называют гипотезу H₁, которая противоречит нулевой.

Пример 6.2.2. Если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а¹10. Коротко это записывают так: H₀: a=10; H₁: a¹10.

Различают гипотезы, которые содержат только одно и гипотезы, содержащие более одного предложения.

Определение 6.2.4. Простой называют гипотезу, содержащую только одно предложение.

Определение 6.2.5. Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.

Пример 6.2.3. Если l – параметр распределения Пуассона, то гипотеза Н₀: l=5 – простая. Сложная гипотеза Н₀: l>5 состоит из бесчисленного множества простых гипотез вида Н_0i: l=b_i , где b_i – любое число, большее 5.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Поскольку проверку проводят статистическими методами, ее называют статистической. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.

Определение 6.2.6. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Определение 6.2.7. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Примечание. Правильное решение может быть принято также в двух случаях:

1) гипотеза принимается, причем в действительности она правильная;

2) гипотеза отвергается, причем в действительности она неверна.

Вероятность совершить ошибку первого рода обозначают через a и называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу).

Вероятность (1–b) не допустить ошибку второго рода, т.е. отвергнуть нулевую гипотезу, когда она неверна, называется мощностью критерия.

Для проверки нулевой гипотезы используют специально подобранную величину, точное или приближенное значение которой известно.

Определение 6.2.8. Статистическим критерием (или просто критерием) называют случайную величину К, которая служит для проверки нулевой гипотезы.

Для проверки гипотезы по данным выборок вычисляют частные значения входящих в критерий величин и таким образом получают частное (наблюдаемое) значение критерия.

Определение 6.2.9. Наблюдаемым значением K_набл называют значение критерия, вычисленное по выборкам.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая – значения критерия, при которых она принимается.

Определение 6.2.10. Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Определение 6.2.11. Областью принятия гипо­тезы (областью допустимых значений) называют совокуп­ность значений критерия, при которых гипотезу принима­ют.

Основной принцип провер­ки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принад­лежит области принятия гипотезы – гипотезу принимают.

Поскольку критерий К – одномерная случайная вели­чина, все ее возможные значения принадлежат некоторому интервалу. Поэтому критическая область и область при­нятия гипотезы также являются интервалами и, следо­вательно, существуют точки, которые их разделяют.

Определение 6.2.12. Критическими точками (границами) k_кp называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или лево­стороннюю) и двустороннюю критические области.

Определение 6.2.13. Правосторонней называют критическую область, опре­деляемую неравенством K>k_кp, где k_кр — положительное число (рис. 6.10, а).

Определение 6.2.14. Левосторонней называют критическую область, опре­деляемую неравенством K < k_кр, где k_кр – отрицательное число (рис. 6.10, б).

Определение 6.2.15.Односторонней называют правостороннюю или лево­стороннюю критическую область.

Определение 6.2.16. Двусторонней называют критическую область, опреде­ляемую неравенствами К<k₁,K>k₂, где k₂> k₁.

В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что k_кр > 0): К<–k_кр, K>k_кр, или равносильным неравенством |К|>k_kp (рис. 6.10, в).

Для отыскания критической области задаются достаточно малой вероятностью – уровнем значимости a и ищут критические точки, исходя из следующих отношений:

а) для правосторонней критической области

Р(K>k_кр)= a (k_кр>0);

б) для левосторонней критической области

Р(K<k_кр)= a (k_кр<0);

в) для двусторонней симметричной области

Р(K>k_кр)= 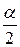Р(K<–k_кр)= 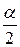, (k_кр>0).

Требования а) - в) определяют значения критерия, при которых нулевая гипотеза отвергается.

Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку, удовлетворяющую этому требованию.