Неравенства с одной переменной (часть II).
Неравенства, содержащие знак модуля.
1º. При решении неравенств, содержащих неизвестные под знаком модуля, используется определение модуля, что приводит к рассмотрению двух случаев:
а) f(x) ≥ 0, тогда |f(x)| = f(x);
б) f(x)<0, тогда |f(x)| = -f(x).
2º. При решении неравенств вида |f(x)| < a или |f(x)| > b полезно использовать следующие соотношения:
1) неравенство вида |f(x)| < a (или |f(x)| ≤ a), где a > 0, равносильно двойному неравенству –a < f(x) < a (или –a ≤ f(x) ≤ a);
2) неравенство вида |f(x)| > b (или |f(x)| ≥ b), где b > 0, равносильно совокупности двух неравенств 
 .
.
3º. Для решения неравенств вида |f(x)| > |g(x)| используют метод возведения в квадрат обеих частей неравенства:

Пример 13. Решить неравенство  .
.
Решение: Возведя обе части неравенства в квадрат, получим неравенство, равносильное данному:  . Преобразовав последнее неравенство, получим
. Преобразовав последнее неравенство, получим  , откуда находим: x ≤ - 2 , x ≥ 0.
, откуда находим: x ≤ - 2 , x ≥ 0.
Ответ:  .
.
4º. Для решения неравенств вида  часто применяют «метод промежутков». Находят ОДЗ неравенства, затем находят корни совокупности уравнений
часто применяют «метод промежутков». Находят ОДЗ неравенства, затем находят корни совокупности уравнений  .
.
Эти корни разбивают ОДЗ на некоторое число промежутков. На каждом промежутке |fi(x)|=fi(x) или |fi(x)|=-fi(x), i=1,2,…,n. Поэтому на каждом из них данное неравенство заменяется на другое неравенство, уже не содержащее знаков модуля и равносильное данному неравенству на этом промежутке. Затем решают полученные неравенства (каждое на своем промежутке). Объединение всех найденных решений дает решение исходного неравенства.
Пример 14. Решить неравенство  .
.
Решение:


Решение первой системы:  ; второй:
; второй:  ; третьей:
; третьей:  . Объединяя, получим
. Объединяя, получим  .
.
Множество значений функции.
1º. Множеством (областью) значений E(y) функции y=f(x) называется множество всех таких чисел y0, для каждого из которых найдется число x0 такое, что f(x0)=y0.
2º. Областью значений всякого многочлена четной степени является промежуток 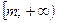 , где m – наименьшее значение этого многочлена, либо промежуток
, где m – наименьшее значение этого многочлена, либо промежуток 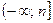 , где n – наибольшее значение этого многочлена.
, где n – наибольшее значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
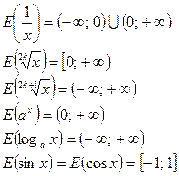
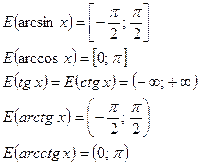
Пример 15. Найти множество значений функции 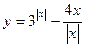 , если x≤1.
, если x≤1.
Решение: Данная функция не определена при x=0 и, следовательно, задана на множестве 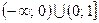 .
.
Рассмотрим x<0, тогда |x|=-x и функция принимает вид 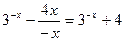 . Так как
. Так как 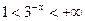 для x<0, то
для x<0, то 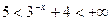 . Таким образом, на промежутке
. Таким образом, на промежутке 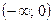 функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то |x|=x и функция имеет вид 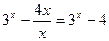 . Так как
. Так как 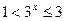 для
для 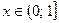 , то
, то 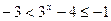 .
.
Ответ: 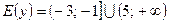 .
.
Дидактический материал.
Решите неравенства:
1. 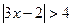 ; 2.
; 2. 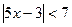 ; 3.
; 3. 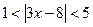 ;
;
4. 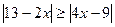 ; 5.
; 5. 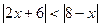 ; 6.
; 6. 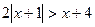 ;
;
7. 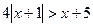 ; 8.
; 8. 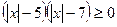 ; 9.
; 9. 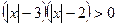 ;
;
10. 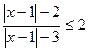 ; 11.
; 11. 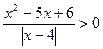 ; 12.
; 12. 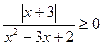 ;
;
13. 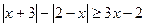 ; 14.
; 14. 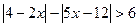 ;
;
15. 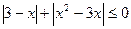 ; 16.
; 16. 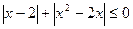 ;
;
17. 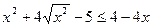 ; 18.
; 18. 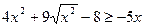 .
.
19. При каких x точки графика функции 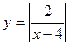 лежат выше прямой
лежат выше прямой 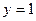 ?
?
20. При каких x точки графика 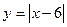 лежат не ниже точек графика функции
лежат не ниже точек графика функции 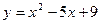 ?
?
Найти множество значений функции:
21. 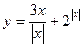 , если
, если 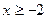 ; 22.
; 22. 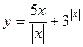 , если
, если 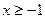 .
.
Тема №6.
Иррациональные уравнения.
1º. Иррациональным называют уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степень состоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду 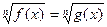 ;
;
б) возводят обе части полученного уравнения в n-ую степень: 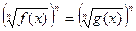 ;
;
в) учитывая, что 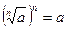 , получают уравнение
, получают уравнение 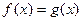 и решают его.
и решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней путем их подстановки в исходное уравнение.
Пример 16. Решить уравнение 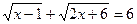 .
.
Решение: Преобразуем уравнение к виду 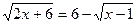 и возведем обе части его в квадрат. Получим:
и возведем обе части его в квадрат. Получим:
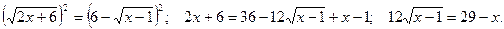
Еще раз возведем обе части уравнения в квадрат:
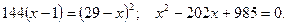
Откуда получим: 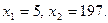
Проверка: 1) При x=5 имеем: 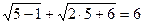 . Таким образом, x=5 является корнем заданного уравнения.
. Таким образом, x=5 является корнем заданного уравнения.
2) 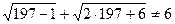 . Таким образом, x=197 – посторонний корень.
. Таким образом, x=197 – посторонний корень.
Ответ: 5.
4º. Метод замены переменной продемонстрируем на примере.
Пример 17. Решить уравнение 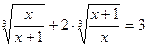 .
.
Решение: Область определения уравнения: 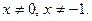 Пусть
Пусть 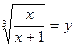 , тогда
, тогда 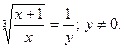 Поэтому
Поэтому 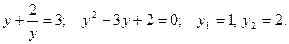 Отсюда:
Отсюда:
1) 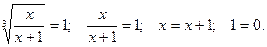 Получили неверное числовое равенство, значит, в этом случае нет корней.
Получили неверное числовое равенство, значит, в этом случае нет корней.
2) 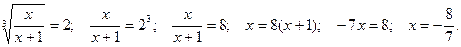
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. 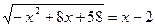 ; 2.
; 2. 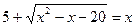 ;
;
3. 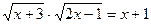 ; 4.
; 4. 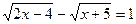 ;
;
5. 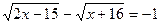 ; 6.
; 6. 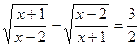 ;
;
7. 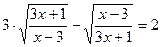 ; 8.
; 8. 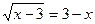 ;
;
9. 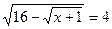 ; 10.
; 10. 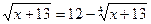 .
.
Найдите наименьший корень уравнения:
11. 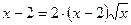 ; 12.
; 12. 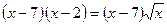 ;
;
13. 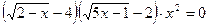 .
.
Найдите произведение всех корней уравнения:
14. 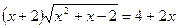 ; 15.
; 15. 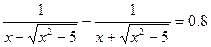 .
.
Решите уравнения:
16. 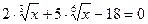 ; 17.
; 17. 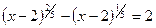 ;
;
18. 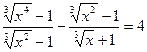 .
.
Тема №7.
Показательные уравнения.
