Уравнения с одной переменной. Равносильность уравнений.

1º. Равенство функций 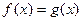называется уравнением с одной переменной.

Множество всех значений неизвестного х, при которых одновременно имеют смысл выражения f(x) и g(x), называется областью определения или областью допустимых значений (ОДЗ) уравнения. Чтобы найти ОДЗ уравнения, необходимо найти пересечение областей определения функций f(x) и g(x).

Число х из ОДЗ уравнения называется корнем ( или решением) уравнения, если при подстановке его в уравнение вместо неизвестного уравнение обращается в верное числовое равенство. Решить уравнение – значит найти множество его корней или доказать, что их нет.

2º. Два уравнения называются равносильными (или эквивалентными), если множества их решений совпадают.

Процесс решения уравнения, в идеале, это цепочка переходов от исходного уравнения к равносильным, приводящая с помощью равносильных преобразований к такому уравнению, для которого множество решений может быть найдено. В общем случае над уравнениями можно выполнять только такие преобразования, которые не нарушают равносильности или нарушают ее, приводя к приобретению посторонних корней. Последние должны быть выявлены путем проверки и отброшены.

Решение уравнений с одним неизвестным, сводящихся к линейным.

1º. Линейным уравнением или уравнением первой степени называется уравнение вида 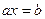, где a и b – действительные числа.

Для линейного уравнения 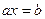могут представиться три случая:

1) a ≠ 0; в этом случае корень уравнения ;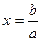

2) a = 0, b ≠ 0; тогда получаем уравнение 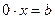, которое не имеет корней;

3) a = 0, b = 0; тогда получаем уравнение 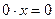, решением которого является любое действительное число, т.е. .

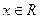2º. Уравнения, сводящиеся к линейным, в т.ч. уравнения вида , обычно решают так:

1) приводят слагаемые (члены уравнения) к общему знаменателю;

2) переносят члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестного, в правую;

3) приводят подобные члены;

4) делят обе части уравнения на коэффициент при неизвестном, если он не равен нулю.

Квадратные уравнения.

1º. Уравнение вида 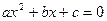, где a,b,c – действительные числа, причем а ≠ 0, называют квадратным уравнением.

Корни квадратного уравнения 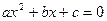находят по формуле:

.

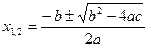Если коэффициент а = 1, то квадратное уравнение называют приведенным; если коэффициент а ≠ 1 – неприведенным.

2º. Выражение 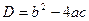называют дискриминантом квадратного уравнения.

Если D < 0, то уравнение 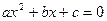не имеет действительных корней; если D = 0, то уравнение имеет один действительный корень (или два одинаковых корня); если D > 0, уравнение имеет два различных действительных корня.

3º. Теорема Виета. Сумма корней квадратного уравнения равна 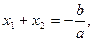а произведение корней равно .

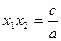Для корней x₁ и x₂ приведенного квадратного уравнения 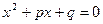формулы Виета имеют вид:

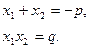
4º. Уравнения вида 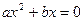, , 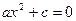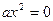называют неполными квадратными уравнениями.

Неполные квадратные уравнения решают следующим образом:

1) ;

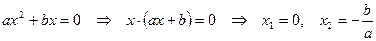2) .

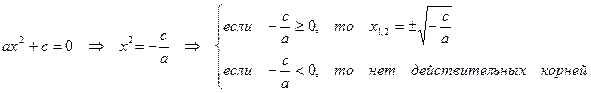5º. Выражение 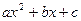называется квадратным трехчленом относительно х.

Квадратный трехчлен 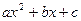может быть разложен на линейные множители по формуле:

,

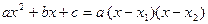где x₁ и x₂ – корни квадратного трехчлена, т.е. корни уравнения 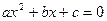(если уравнение имеет действительные корни).