Арифметические вычисления. Проценты.
Тема №1.
Арифметические вычисления. Проценты.
Дидактический материал.
Найдите значение выражения:
1) 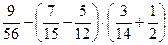 ; 2)
; 2) 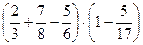 ;
;
3) 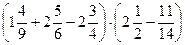 ; 4)
; 4) 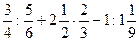 ;
;
5) 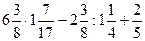 ; 6)
; 6) 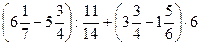 ;
;
7) 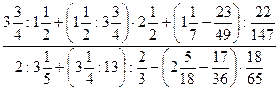 ;
;
8) 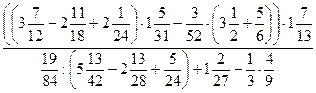 .
.
Ответы: 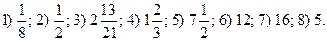
Десятичные дроби. Действия над десятичными дробями.
1º. Обыкновенную дробь со знаменателем 10, 100, 1000 и т.д., записанную без знаменателя, называют десятичной дробью.
Например, 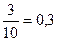 ;
; 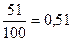 ;
; 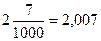 .
.
2º. Правила арифметических действий над десятичными дробями:
a) При сложении (вычитании) десятичных дробей надо записать их одну под другой так, чтобы одинаковые разряды были друг под другом, а запятая под запятой и сложить (вычесть) их как натуральные числа, не забыв поставить в результате запятую под запятыми.
b) Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, и в полученном произведении отделить справа запятой столько цифр, сколько их стоит после запятой в обоих множителях вместе. Если цифр в полученном произведении недостаточно, то приписывают слева нули.
Например, 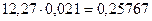 .
.
c) При делении десятичной дроби на натуральное число надо разделить это число, не обращая внимания на запятую, и поставить в частном запятую, когда закончится деление целой части.
Например, 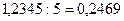 .
.
d) Чтобы разделить число на десятичную дробь, нужно в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, а потом выполнить деление на натуральное число. Если в делимом меньше десятичных знаков, чем в делителе, то справа приписывают необходимое количество нулей.
Например, 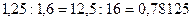 .
.
e) При умножении (делении) десятичной дроби на 10,100, 1000 и т.д. достаточно перенести запятую вправо (влево) на столько цифр, сколько нулей во множителе (делителе).
Например, 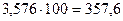 ;
; 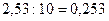 .
.
3º. При выполнении совместных действий с обыкновенными и десятичными дробями нужно учитывать рациональность выбора: иногда лучше действия выполнить в - обыкновенных дробях, а в других случаях – в десятичных.
a) Любую обыкновенную дробь можно обратить в десятичную (конечную или бесконечную периодическую), разделив числитель на знаменатель по правилу деления десятичной дроби на натуральное число.
Например, 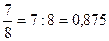 ;
; 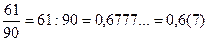 .
.
b) Чтобы обратить конечную десятичную дробь в обыкновенную, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе – единицу с нулями, причем нулей должно быть столько, сколько цифр справа от запятой.
Например, 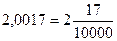 .
.
c) Чтобы обратить бесконечную периодическую десятичную дробь в обыкновенную, надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом.
Например, 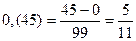 ;
; 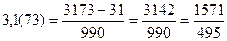 .
.
Дидактический материал.
Найдите значение выражения:
1) 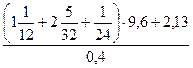 ; 2)
; 2) 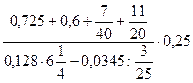 ;
;
3) 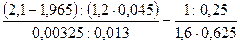 ; 4)
; 4) 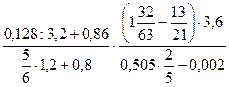 ;
;
5) 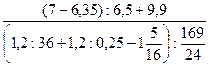 ; 6)
; 6) 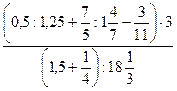 ;
;
7) 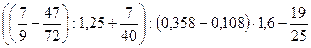 ;
;
8) 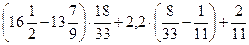 ; 9)
; 9) 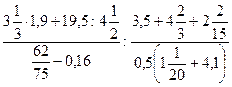 ;
;
10) 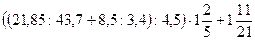 ; 11)
; 11) 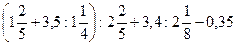 ;
;
12) 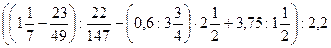 ;
;
13) 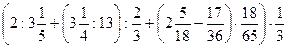 ;
;
14) 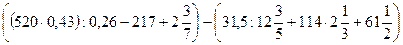 ;
;
15) 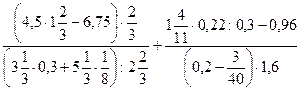 ;
;
16) 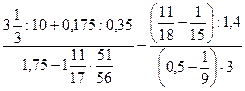 ; 17)
; 17) 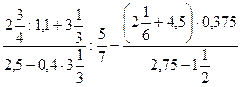 ;
;
18) 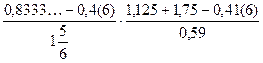 ; 19)
; 19) 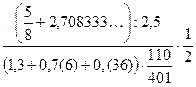 ;
;
20) 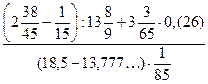 .
.
Найти Х из пропорции:
21) 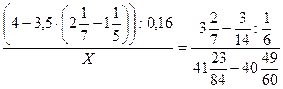 ;
;
22) 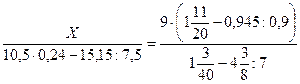 ;
;
23) 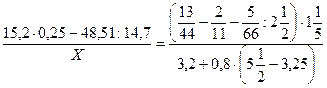 ;
;
24) 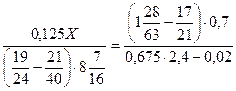 .
.
Ответы: 1) 84,075; 2) 1; 3) 6; 4) 8; 5) 20; 6) 32; 7) 1; 8) 2; 9) 4; 10) 2; 11) 3; 12) 3; 13) 0,5; 14) 3; 15) 1; 16) 3; 17) 5; 18) 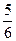 ; 19) 1; 20) 9; 21) 1; 22) 5; 23) 25; 24) 5.
; 19) 1; 20) 9; 21) 1; 22) 5; 23) 25; 24) 5.
Дидактический материал.
1) Найдите:
а) 4% от 75; б) 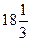 % от 330; в) 160% от 82,25.
% от 330; в) 160% от 82,25.
2) Найдите число, если:
а) 40% его равны 12; б) 1,25 % его равны 55; в) 0,8% его равны 1,84; г) 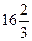 % его равны
% его равны 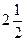 .
.
3) Найти, сколько процентов составляет:
а) число 15,57 от числа 90; б) число 150 от числа 120; в) число 0,3 от 1,9
4) Число, 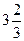 % которого составляют
% которого составляют 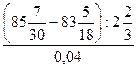 , равно:
, равно:
а) 0,672 б) 400 в) 672 г) 500 д) 472
5) Число, 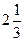 % которого составляет
% которого составляет 
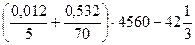 , равно:
, равно:
а) 762 б) 580 в) 140 г) 350 д) 7,62
6) Сколько процентов числа 3 составляет разность между ним и 3% числа 20?
7) 18% числа 10 равны 15% числа с. Найти с.
8) После увеличения числа на 17% получили 108,81. Исходное число равно:
а) 93,05 б) 93 в) 94 г) 92 д) 92,86
9) Некоторое число уменьшили на 14%, получив в результате 95. Это число с точностью до 0,01 равно:
а) 110,46 б) 110,44 в) 109,59 г) 110,50 д) 110,47
10) Сберегательный банк начисляет по вкладам ежегодно 2% вклада. Вкладчик внес в банк 15000 руб. Какой станет сумма через 2 года?
11) По долгосрочному вкладу банк выплачивает 10% годовых. По истечении каждого года начисленная сумма присоединяется к вкладу. На этот вид вклада был открыт счет в 20000 руб., который не пополнялся и с которого не снимали деньги в течение 3-х лет. Какой доход был получен по истечении этого срока?
12) Вкладчику на положенные в банк деньги через год начислили проценты в размере 15 тыс.рублей. Не взяв их, а добавив еще 85 тыс.рублей, он оставил все деньги еще на год под те же проценты. По истечении второго срока вклад вместе с процентными начислениями составил 275 тыс.рублей. Сколько тысяч рублей было положено в банк первоначально? (При решении задачи следует учесть, что процентная ставка банка не может превышать 100% годовых).
13) Вкладчик положил в банк некоторую сумму под 10% годовых. Каждый год после начисления процентов он добавляет на свой счет 5000 рублей. В результате через три года его вклад составил 29860 рублей. Какова была сумма первоначального вклада?
14) Производительность труда второй бригады на 20% больше, чем первой бригады, а производительность труда третьей бригады на 25% меньше, чем второй. На сколько процентов производительность труда третьей бригады меньше, чем первой?
15) Владелец магазина дважды за год повышал центы на товары в среднем на 10%. На сколько процентов повысилась цена на товары за год?
16) Цены на компьютерную технику в среднем понижались за год дважды на 10%. На сколько процентов понизились цены на компьютерную технику за год?
17) Два спиртовых раствора борной кислоты одинаковой массы слили в один сосуд. Раствор какой концентрации получили в результате, если первый раствор был пятипроцентным (5% борной кислоты и 95% спирта), а второй – однопроцентный?
18) Сколько мл воды нужно добавить к 500 мл 96%-ного раствора спирта (96% спирта, 4% воды), чтобы получить 40%-ный раствор спирта?
19) Из сосуда, полностью заполненного 12%-ным раствором соли, отлили 1л и налили 1л воды. После этого в сосуде оказался 9%-ный раствор соли. Сколько литров вмещает сосуд?
20) В библиотеке имеются книги на английском, французском и немецком языках. Английские книги составляют 36% всех книг на иностранных языках. Французские – 75% английских, а остальные 185 книг – немецкие. Сколько книг на иностранных языках в библиотеке?
21) Свежие грибы содержат по массе 90% воды, а сухие – 12%. Сколько получится сухих грибов из 44 кг свежих?
Ответы: 6) 80%; 7) 12; 10) 15660; 11) 15606; 12) 150; 13) 10000; 14) 10; 15) 21; 16) 19; 17) 3; 18) 700; 19) 4; 20) 500; 21) 5.
Тема №2.
Уравнения. Модуль числа.
Квадратные уравнения.
1º. Уравнение вида 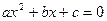 , где a,b,c – действительные числа, причем а ≠ 0, называют квадратным уравнением.
, где a,b,c – действительные числа, причем а ≠ 0, называют квадратным уравнением.
Корни квадратного уравнения 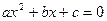 находят по формуле:
находят по формуле:
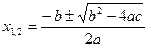 .
.
Если коэффициент а = 1, то квадратное уравнение называют приведенным; если коэффициент а ≠ 1 – неприведенным.
2º. Выражение 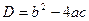 называют дискриминантом квадратного уравнения.
называют дискриминантом квадратного уравнения.
Если D < 0, то уравнение 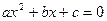 не имеет действительных корней; если D = 0, то уравнение имеет один действительный корень (или два одинаковых корня); если D > 0, уравнение имеет два различных действительных корня.
не имеет действительных корней; если D = 0, то уравнение имеет один действительный корень (или два одинаковых корня); если D > 0, уравнение имеет два различных действительных корня.
3º. Теорема Виета. Сумма корней квадратного уравнения равна 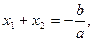 а произведение корней равно
а произведение корней равно 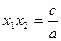 .
.
Для корней x1 и x2 приведенного квадратного уравнения 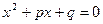 формулы Виета имеют вид:
формулы Виета имеют вид:
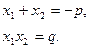
4º. Уравнения вида 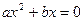 ,
, 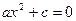 ,
, 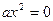 называют неполными квадратными уравнениями.
называют неполными квадратными уравнениями.
Неполные квадратные уравнения решают следующим образом:
1) 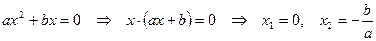 ;
;
2) 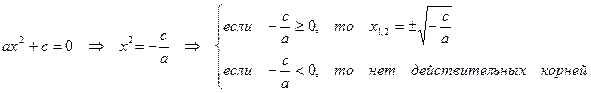 .
.
5º. Выражение 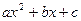 называется квадратным трехчленом относительно х.
называется квадратным трехчленом относительно х.
Квадратный трехчлен 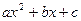 может быть разложен на линейные множители по формуле:
может быть разложен на линейные множители по формуле:
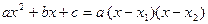 ,
,
где x1 и x2 – корни квадратного трехчлена, т.е. корни уравнения 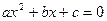 (если уравнение имеет действительные корни).
(если уравнение имеет действительные корни).
Дидактический материал.
Решите уравнения, сводящиеся к линейным:
1. 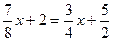 ; 2.
; 2. 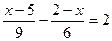 ; 3.
; 3. 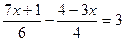 ;
;
4. 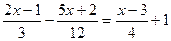 ; 5.
; 5. 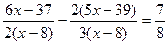 ;
;
6. 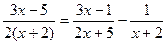 ; 7.
; 7. 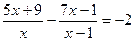 ;
;
8. 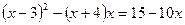 ; 9.
; 9. 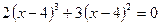 ;
;
10. 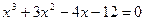 ; 11.
; 11. 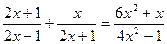 .
.
Решите квадратные уравнения:
12. 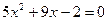 ; 13.
; 13. 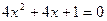 ;
;
14. 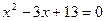 ; 15.
; 15. 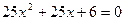 ;
;
16. 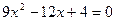 .
.
Разложите на линейные множители:
17. 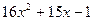 ; 18.
; 18. 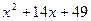 ; 19.
; 19. 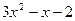 ;
;
20. 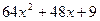 ; 21.
; 21. 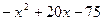 .
.
Сократите дроби:
22. 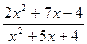 ; 23.
; 23. 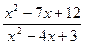 ; 24.
; 24. 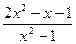 ;
;
25. 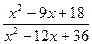 ; 26.
; 26. 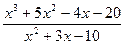 ; 27.
; 27. 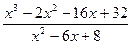 .
.
Упростите выражение:
28. 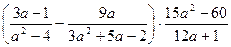 ; 29.
; 29. 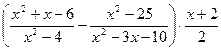 .
.
Найдите среднее арифметическое всех действительных корней уравнения:
30. 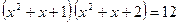 ; 31.
; 31. 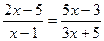 ;
;
32. 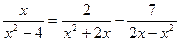 ; 33.
; 33. 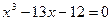 ;
;
34. 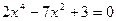 ; 35.
; 35. 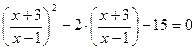 ;
;
36. 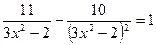 .
.
Найдите расстояние от вершины параболы до точки М:
37. 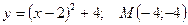 ; 38.
; 38. 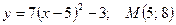 ;
;
39. 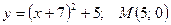 ; 39.
; 39. 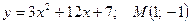 .
.
Постройте график функции:
40. 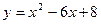 ; 41.
; 41. 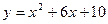 ; 42.
; 42. 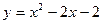 ;
;
43. 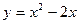 ; 44.
; 44. 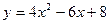 ; 45.
; 45. 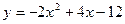 ;
;
46. 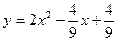 ; 47.
; 47. 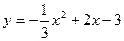 ; 48.
; 48. 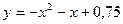 ;
;
49. 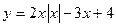 ; 50.
; 50. 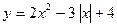 ; 51.
; 51. 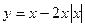 .
.
52. По графику квадратичной функции определить знаки ее коэффициентов и их суммы:
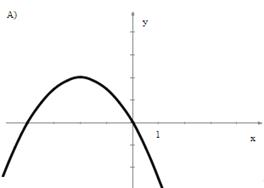
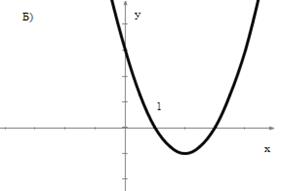
Найдите рациональные корни уравнения:
53. 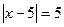 ; 54.
; 54. 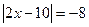 ; 55.
; 55. 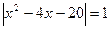 ;
;
56. 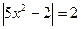 ; 57.
; 57. 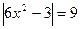 ; 58.
; 58. 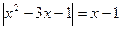 ;
;
59. 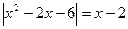 ; 60.
; 60. 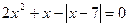 ; 61.
; 61. 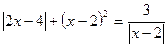 .
.
Решите уравнения:
62. 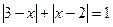 ; 63.
; 63. 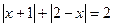 ; 64.
; 64. 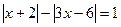 ;
;
65. 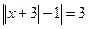 ; 66.
; 66. 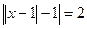 ; 67.
; 67. 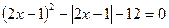 ;
;
68. 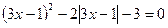 ; 69.
; 69. 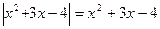 ;
;
70. 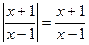 ; 71.
; 71. 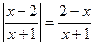 ; 72.
; 72. 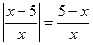 .
.
Тема №3.
Степени и корни.
Дидактический материал.
Вычислите:
1. 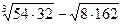 ; 2.
; 2. 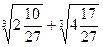 ; 3.
; 3. 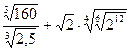 ;
;
4. 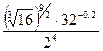 ; 5.
; 5. 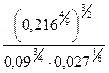 ; 6.
; 6. 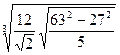 ;
;
7. 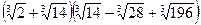 ; 8.
; 8. 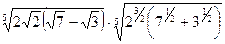 ;
;
9. 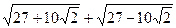 ; 10.
; 10. 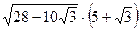 ;
;
11. 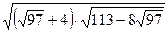 ; 12.
; 12. 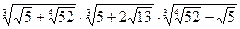 ;
;
13. 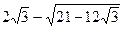 ; 14.
; 14. 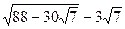 ; 15.
; 15. 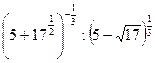 .
.
Внесите множители под знак общего корня:
16. 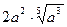 ; 17.
; 17. 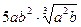 ; 18.
; 18. 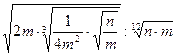 .
.
Упростите выражения:
19. 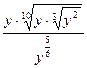 ; 20.
; 20. 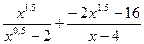 ; 21.
; 21. 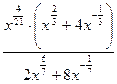 ;
;
22. 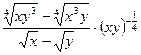 ; 23.
; 23. 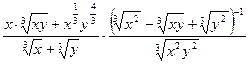 ;
;
24. 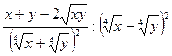 ; 25.
; 25. 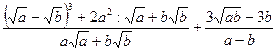 ;
;
26. 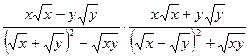 ;
;
27. 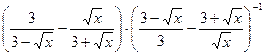 .
.
Ответы: 19. 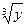 ; 20. x + 4; 21. 0,5; 22. -1; 23.
; 20. x + 4; 21. 0,5; 22. -1; 23. 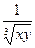 ; 24. 1; 25. 3; 26. x – y;
; 24. 1; 25. 3; 26. x – y;
27. 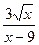 .
.
Тема №4.
Метод интервалов.
1º. Если дискриминант квадратного трехчлена D > 0 или D = 0, то квадратное неравенство 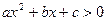 можно переписать в виде
можно переписать в виде 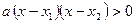 или
или 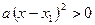 , где x1 и x2 – корни квадратного трехчлена, и использовать для его решения метод интервалов.
, где x1 и x2 – корни квадратного трехчлена, и использовать для его решения метод интервалов.
2º. Для решения любых алгебраических уравнений
вида (1) 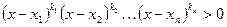 или вида (2)
или вида (2) 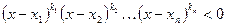 , где x1, x2, …, xn – действительные числа, удовлетворяющие условию x1 < x2 < …< xn, а k1, k2, …, kn – натуральные числа, применим обобщенный метод интервалов.
, где x1, x2, …, xn – действительные числа, удовлетворяющие условию x1 < x2 < …< xn, а k1, k2, …, kn – натуральные числа, применим обобщенный метод интервалов.
Суть его состоит в следующем: на координатной оси отмечают числа x1, x2, …, xn, в промежутке справа от xn ставят знак +,
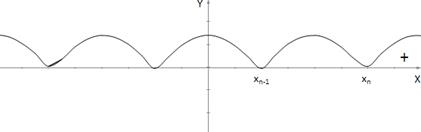
затем, двигаясь справа налево, при переходе через очередную точку xi меняют знак, если ki - нечетное число и сохраняют знак, если ki - четное число. Тогда множеством решений неравенства (1) будет объединение промежутков, в каждом из которых поставлен знак +, а множеством решений неравенства (2) будет объединение промежутков, в каждом из которых поставлен знак – .
Замечание. Обобщенный метод интервалов справедлив и для целых рациональных неравенств P(x) > 0 или Q(x) ≥ 0, и для дробно-рациональных неравенств 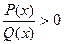 или
или 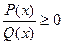 , причем последние равносильны неравенству
, причем последние равносильны неравенству 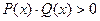 и системе
и системе 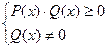 соответственно, где P(x), Q(x) – некоторые многочлены.
соответственно, где P(x), Q(x) – некоторые многочлены.
Пример 11. Решить неравенство 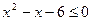 .
.
Решение: Находим корни квадратного трехчлена 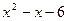 :
:
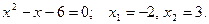 Данное неравенство равносильно следующему неравенству:
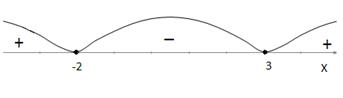
Данное неравенство равносильно следующему неравенству: 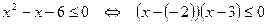 . Применяя метод интервалов к последнему неравенству, получим множество всех решений неравенства – отрезок [-2; 3].
. Применяя метод интервалов к последнему неравенству, получим множество всех решений неравенства – отрезок [-2; 3].
Ответ: 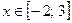 .
.
Пример 12. Решить неравенство 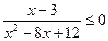 .
.
Решение:
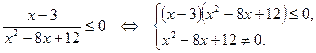
Находим корни числителя и знаменателя: 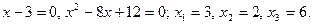
Указанная система равносильна следующей системе: 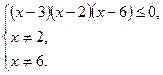
Нанесем найденные корни на числовую прямую. В интервалах справа налево расставим знаки плюс и минус.
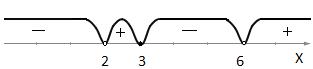
Множеством всех решений данного неравенства является объединение промежутков, в которых поставлен знак минус.
Ответ: 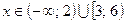 .
.
Дидактический материал.
Решите неравенства:
1. 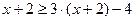 ; 2.
; 2. 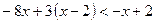 ;
;
3. 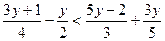 ; 4.
; 4. 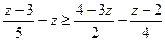 .
.
Решите системы неравенств:
5. 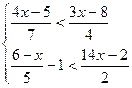 ; 6.
; 6. 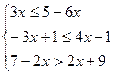 .
.
Найдите целые решения системы неравенств:
7. 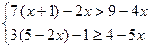 ; 8.
; 8. 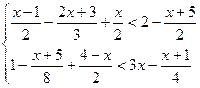 .
.
Решите неравенства:
9. 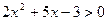 ; 10.
; 10. 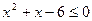 ; 11.
; 11. 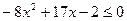 ;
;
12. 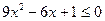 ; 13.
; 13. 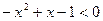 ;
;
14. 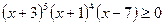 ; 15.
; 15. 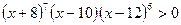 ;
;
16. 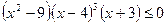 ; 17.
; 17. 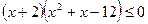 ;
;
18. 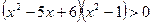 ; 19.
; 19. 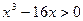 ;
;
20. 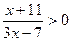 ; 21.
; 21. 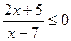 ; 22.
; 22. 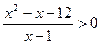 ;
;
23. 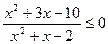 ; 24.
; 24. 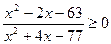 ;
;
25. 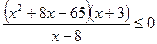 ; 26.
; 26. 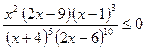 ;
;
27. 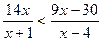 ; 28.
; 28. 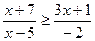 ; 29.
; 29. 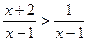 ;
;
30. 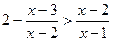 ; 31.
; 31. 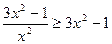 ; 32.
; 32. 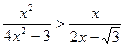 .
.
Тема №5.
Множество значений функции.
1º. Множеством (областью) значений E(y) функции y=f(x) называется множество всех таких чисел y0, для каждого из которых найдется число x0 такое, что f(x0)=y0.
2º. Областью значений всякого многочлена четной степени является промежуток 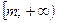 , где m – наименьшее значение этого многочлена, либо промежуток
, где m – наименьшее значение этого многочлена, либо промежуток 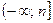 , где n – наибольшее значение этого многочлена.
, где n – наибольшее значение этого многочлена.
Областью значений всякого многочлена нечетной степени является R.
3º. Области значений основных элементарных функций:
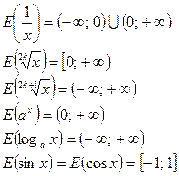
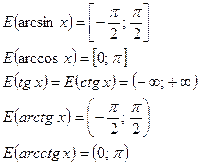
Пример 15. Найти множество значений функции 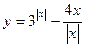 , если x≤1.
, если x≤1.
Решение: Данная функция не определена при x=0 и, следовательно, задана на множестве 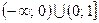 .
.
Рассмотрим x<0, тогда |x|=-x и функция принимает вид 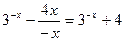 . Так как
. Так как 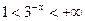 для x<0, то
для x<0, то 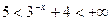 . Таким образом, на промежутке
. Таким образом, на промежутке 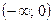 функция принимает значения от 5 до +∞.
функция принимает значения от 5 до +∞.
Если x>0, то |x|=x и функция имеет вид 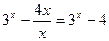 . Так как
. Так как 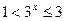 для
для 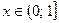 , то
, то 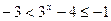 .
.
Ответ: 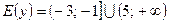 .
.
Дидактический материал.
Решите неравенства:
1. 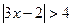 ; 2.
; 2. 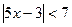 ; 3.
; 3. 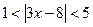 ;
;
4. 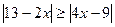 ; 5.
; 5. 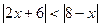 ; 6.
; 6. 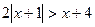 ;
;
7. 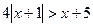 ; 8.
; 8. 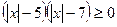 ; 9.
; 9. 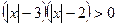 ;
;
10. 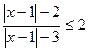 ; 11.
; 11. 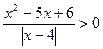 ; 12.
; 12. 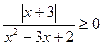 ;
;
13. 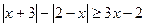 ; 14.
; 14. 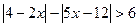 ;
;
15. 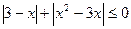 ; 16.
; 16. 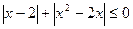 ;
;
17. 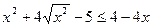 ; 18.
; 18. 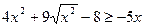 .
.
19. При каких x точки графика функции 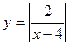 лежат выше прямой
лежат выше прямой 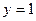 ?
?
20. При каких x точки графика 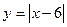 лежат не ниже точек графика функции
лежат не ниже точек графика функции 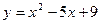 ?
?
Найти множество значений функции:
21. 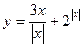 , если
, если 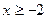 ; 22.
; 22. 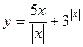 , если
, если 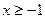 .
.
Тема №6.
Иррациональные уравнения.
1º. Иррациональным называют уравнение, в котором переменная содержится под знаком корня.
При решении иррациональных уравнений применяют 2 метода: метод возведения в степень обеих частей уравнения и метод введения новой переменной (замены переменной).
2º. Метод возведения обеих частей уравнения в одну и ту же степень состоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду 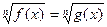 ;
;
б) возводят обе части полученного уравнения в n-ую степень: 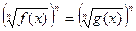 ;
;
в) учитывая, что 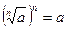 , получают уравнение
, получают уравнение 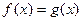 и решают его.
и решают его.
3º. Следует учитывать, что при возведении обеих частей уравнения в четную степень возможно появление посторонних корней. В этом случае обязательна проверка найденных корней путем их подстановки в исходное уравнение.
Пример 16. Решить уравнение 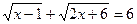 .
.
Решение: Преобразуем уравнение к виду 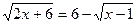 и возведем обе части его в квадрат. Получим:
и возведем обе части его в квадрат. Получим:
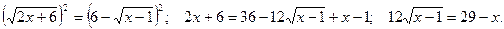
Еще раз возведем обе части уравнения в квадрат:
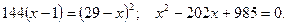
Откуда получим: 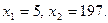
Проверка: 1) При x=5 имеем: 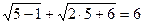 . Таким образом, x=5 является корнем заданного уравнения.
. Таким образом, x=5 является корнем заданного уравнения.
2) 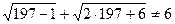 . Таким образом, x=197 – посторонний корень.
. Таким образом, x=197 – посторонний корень.
Ответ: 5.
4º. Метод замены переменной продемонстрируем на примере.
Пример 17. Решить уравнение 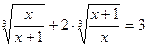 .
.
Решение: Область определения уравнения: 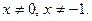 Пусть
Пусть 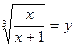 , тогда
, тогда 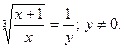 Поэтому
Поэтому 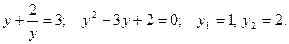 Отсюда:
Отсюда:
1) 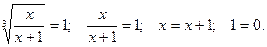 Получили неверное числовое равенство, значит, в этом случае нет корней.
Получили неверное числовое равенство, значит, в этом случае нет корней.
2) 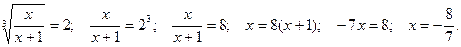
Ответ: -8/7.
Дидактический материал.
Решите уравнения:
1. 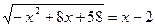 ; 2.
; 2. 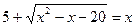 ;
;
3. 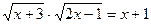 ; 4.
; 4. 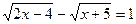 ;
;
5. 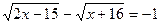 ; 6.
; 6. 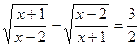 ;
;
7. 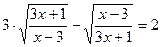 ; 8.
; 8. 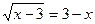 ;
;
9. 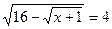 ; 10.
; 10. 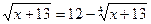 .
.
Найдите наименьший корень уравнения:
11. 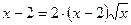 ; 12.
; 12. 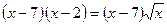 ;
;
13. 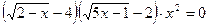 .
.
Найдите произведение всех корней уравнения:
14. 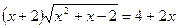 ; 15.
; 15. 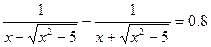 .
.
Решите уравнения:
16. 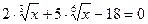 ; 17.
; 17. 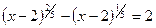 ;
;
18. 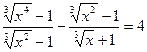 .
.
Тема №7.
Показательные уравнения.
Дидактический материал.
Решите уравнения:
1. 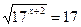 ; 2.
; 2. 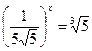 ; 3.
; 3. 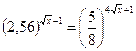 ;
;
4. 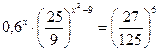 ; 5.
; 5. 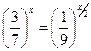 ; 6.
; 6. 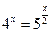 ;
;
7. 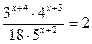 ; 8.
; 8. 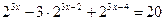 ;
;
9. 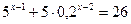 ; 10.
; 10. 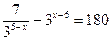 ; 11.
; 11. 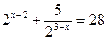 ;
;
12. 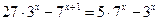 ; 13.
; 13. 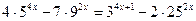 ;
;
14. 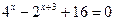 ; 15.
; 15. 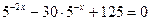 ;
;
16. 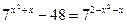 ; 17.
; 17. 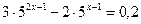 ;
;
18. 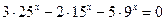 ; 19.
; 19. 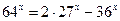 ;
;
20. 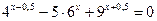 ; 21.
; 21. 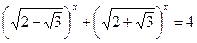 ;
;
22. 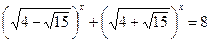 ; 23.
; 23. 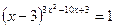 ;
;
24. 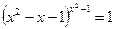 ; 25.
; 25. 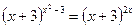 .
.
26. Найдите произведение корней уравнения 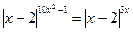 .
.
27. Найдите сумму корней уравнения 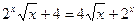 .
.
Найдите значение выражения:
28. 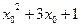 , где x0 – корень уравнения
, где x0 – корень уравнения 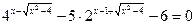 ;
;
29. 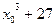 , где x0 – целый корень уравнения
, где x0 – целый корень уравнения 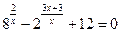 .
.
Решите уравнение:
30. 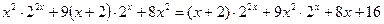 ;
;
31. 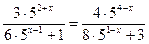 ; 32.
; 32. 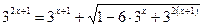 .
.
Ответы: 1. 0; 2. -2/9; 3. 1/36; 4. 0, 0.5; 5. 0; 6. 0; 7. -2; 8. 2; 9. 1, 3; 10. 8; 11. 5; 12. 1; 13. ¼; 14. 2; 15. -2, -1; 16. -2, 1; 17. 0; 18. 1; 19. 0; 20. -1, 0; 21. -2, 2; 22. -2, 2; 23. 4; 24. -1, 2; 25. -2, -1, 3; 26. -0.3; 27. 3; 28. 11; 29. 54; 30. -1, 0, 2, 3; 31. 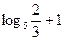 ; 32.
; 32. 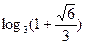 .
.
Тема №8.
Показательные неравенства.
1º. Неравенство, содержащее переменную в показателе степени, называется показательным неравенством.
2º. Решение показательных неравенств вида 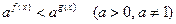 основано на следующих утверждениях:
основано на следующих утверждениях:
если 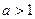 , то неравенство
, то неравенство 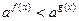 равносильно
равносильно 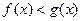 ;
;
если 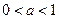 , то неравенство
, то неравенство 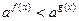 равносильно
равносильно 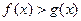 .
.
При решении показательных неравенств используют те же приемы, что и при решении показательных уравнений.
Пример 26. Решить неравенство 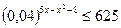 (методом перехода к одному основанию).
(методом перехода к одному основанию).
Решение: Так как 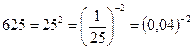 , то заданное неравенство можно записать в виде:
, то заданное неравенство можно записать в виде: 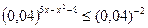 . Так как
. Так как 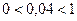 , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству 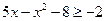 .
.
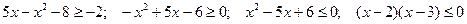 .
.
Решив последнее неравенство, получим 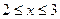 .
.
Ответ: 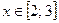 .
.
Пример 27. Решить неравенство: 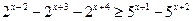 (методом вынесения общего множителя за скобки).
(методом вынесения общего множителя за скобки).
Решение: Вынесем за скобки в левой части неравенства 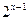 , в правой части неравенства
, в правой части неравенства 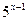 и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
и разделим обе части неравенства на (-2), поменяв знак неравенства на противоположный:
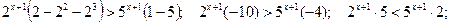
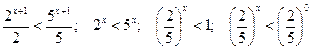 .
.
Так как 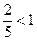 , то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем
, то при переходе к неравенству показателей знак неравенства опять меняется на противоположный. Получаем 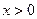 . Таким образом, множество всех решений данного неравенства есть интервал
. Таким образом, множество всех решений данного неравенства есть интервал 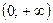 .
.
Ответ: 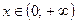 .
.
Пример 28. Решить неравенство 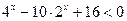 (методом введения новой переменной).
(методом введения новой переменной).
Решение: Пусть 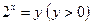 . Тогда данное неравенство примет вид:
. Тогда данное неравенство примет вид: 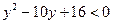 или
или 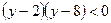 , решением которого является интервал
, решением которого является интервал 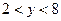 .
.
Отсюда 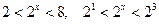 . Поскольку функция
. Поскольку функция 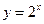 возрастает, то
возрастает, то 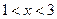 .
.
Ответ: 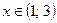 .
.
Дидактический материал.
Укажите множество решений неравенства:
1. 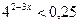 ; 2.
; 2. 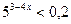 ; 3.
; 3. 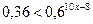 ;
;
4. 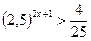 ; 5.
; 5. 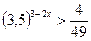 .
.
6. При каких значениях x точки графика функции 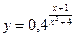 лежат ниже прямой
лежат ниже прямой 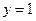 ?
?
7. При каких значениях x точки графика функции 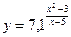 лежат не ниже прямой
лежат не ниже прямой 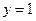 ?
?
Решите неравенство:
8. 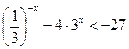 ; 9.
; 9. 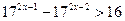 ; 10.
; 10. 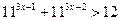 ;
;
11. 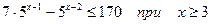 ; 12.
; 12. 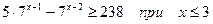 .
.
13. Укажите наибольшее целое решение неравенства 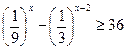 .
.
14. Найдите произведение наибольшего целого и наименьшего целого решений неравенства 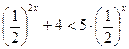 .
.
Решите неравенство:
15. 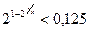 ; 16.
; 16.
