Алгоритмы письменных вычислений в десятичной системе счисления
Алгоритм сложения натуральных чисел, записанных в десятичной системе счисления (алгоритм сложения «столбиком»)
1. Записывают второе слагаемое под первым так, чтобы соответствующие разряды находились друг под другом.
2. Складывают единицы первого разряда. Если сумма меньше десяти, записывают ее в разряд единиц ответа и переходят к следующему разряду (десятков).
3. Если сумма единиц больше или равна десяти, то представляют ее в виде  , где
, где  – однозначное число; записывают
– однозначное число; записывают  в разряд единиц ответа и прибавляют 1 к десяткам первого слагаемого, после чего переходят к разряду десятков.
в разряд единиц ответа и прибавляют 1 к десяткам первого слагаемого, после чего переходят к разряду десятков.
4. Повторяют те же действия с десятками, потом с сотнями и т.д. Процесс заканчивается, когда оказываются сложенными цифры старших разрядов. При этом, если их сумма больше или равна десяти, то приписывают впереди обоих слагаемых нули, увеличивают нуль перед первым слагаемым на 1 и выполняют сложение  .
.
Алгоритм вычитания натуральных чисел, записанных в десятичной системе счисления (алгоритм вычитания «столбиком»)
1. Записывают вычитаемое под уменьшаемым так, чтобы соответствующие разряды находились друг под другом.
2. Если цифра в разряде единиц вычитаемого не превосходит соответствующей цифры уменьшаемого, вычитаем ее из цифры уменьшаемого, записывают разность в разряд единиц искомого числа, после чего переходят к следующему разряду.
3. Если же цифра единиц вычитаемого больше единиц уменьшаемого, т.е.  , а цифра десятков уменьшаемого отлична от нуля, то уменьшают цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитают из числа
, а цифра десятков уменьшаемого отлична от нуля, то уменьшают цифру десятков уменьшаемого на 1, одновременно увеличив цифру единиц уменьшаемого на 10, после чего вычитают из числа  число
число  и записывают разность в разряде единиц искомого числа, далее переходят к следующему разряду.
и записывают разность в разряде единиц искомого числа, далее переходят к следующему разряду.
4. Если цифра единиц вычитаемого больше цифры единиц уменьшаемого, а цифры, стоящие в разряде десятков, сотен и т.д. уменьшаемого, равны нулю, то берут первую отличную от нуля цифру в уменьшаемом (после разряда единиц), уменьшают ее на 1, все цифры в младших разрядах до разряда десятков включительно увеличивают на 9, а цифру в разряде единиц на 10: вычитают  из
из  , записывают разность в разряде единиц искомого числа и переходят к следующему разряду.
, записывают разность в разряде единиц искомого числа и переходят к следующему разряду.
5. В следующем разряде повторяют описанный процесс. Вычитание заканчивается, когда производится вычитание из старшего разряда уменьшаемого.
Алгоритм умножения многозначного числа  на однозначное число y.
на однозначное число y.
1. Записывают второе число под первым.
2. Умножают цифры разряда единиц числа  на число
на число  . Если произведение меньше 10, его записывают в разряд единиц ответа и переходят к следующему разряду (десятков).
. Если произведение меньше 10, его записывают в разряд единиц ответа и переходят к следующему разряду (десятков).
3. Если произведение цифр единиц числа х на число у больше или равно 10, то представляют его в виде  , где
, где  – однозначное число; записывают
– однозначное число; записывают  в разряд единиц ответа и запоминают
в разряд единиц ответа и запоминают  – перенос в следующий разряд.
– перенос в следующий разряд.
4. Умножают цифры разряда десятков на число у, прибавляют к полученному произведению число  и повторяют процесс, описанный в пп. 2 и 3.
и повторяют процесс, описанный в пп. 2 и 3.
5. Процесс умножения заканчивается, когда окажется умноженной цифра старшего разряда.
Алгоритм умножения числа  на число
на число  .
.
1. Записывают множитель x и под ним второй множитель у.
2. Умножают число x на младший разряд  числа у и записывают произведение
числа у и записывают произведение  под числом у.
под числом у.
3. Умножают число х на следующий разряд  , числа у и записывают произведение
, числа у и записывают произведение  , но со сдвигом на один разряд влево, что соответствует умножению
, но со сдвигом на один разряд влево, что соответствует умножению  на 10.
на 10.
4. Продолжают вычисление произведений до вычисления  .
.
5. Полученные  произведения складывают.
произведения складывают.
Алгоритм деления «уголком» целого неотрицательного числа 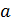 на натуральное число
на натуральное число 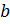
1. Если  , то частное
, то частное  , остаток
, остаток  .
.
2. Если  и число разрядов в числах
и число разрядов в числах 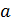 и
и 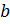 одинаково, то частное
одинаково, то частное  находят перебором, последовательно умножая
находят перебором, последовательно умножая 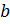 на
на  , так как
, так как  . Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел
. Этот перебор можно ускорить, выполнив деление с остатком цифр старших разрядов чисел 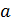 и
и 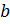 .
.
3. Если  и число разрядов в числе
и число разрядов в числе 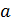 больше, чем в числе
больше, чем в числе 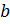 , то записывают делимое
, то записывают делимое 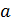 и справа от него делитель
и справа от него делитель 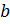 , который отделяют от
, который отделяют от 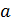 уголком и ведут поиск частного и остатка в такой последовательности:
уголком и ведут поиск частного и остатка в такой последовательности:
а) выделяют в числе  столько старших разрядов, сколько разрядов в числе
столько старших разрядов, сколько разрядов в числе  или, если необходимо, на один разряд больше, но так, чтобы они образовывали число
или, если необходимо, на один разряд больше, но так, чтобы они образовывали число  , больше или равное
, больше или равное  . Перебором находят частное
. Перебором находят частное  чисел
чисел  , и
, и  , последовательно умножая
, последовательно умножая  на
на  . Записывают
. Записывают  под уголком (ниже
под уголком (ниже  );
);
б) умножают  на
на  и записывают произведение под числом
и записывают произведение под числом  так, чтобы младший разряд числа
так, чтобы младший разряд числа  был написан под младшим разрядом выделенного числа
был написан под младшим разрядом выделенного числа  ;
;
в) проводят черту под  и находим разность
и находим разность  ;
;
г) записывают разность  , под числом
, под числом  , приписывают справа к
, приписывают справа к  старший разряд из неиспользованных разрядов делимого
старший разряд из неиспользованных разрядов делимого  и сравнивают полученное число
и сравнивают полученное число  с числом
с числом  ;
;
д) если полученное число  больше или равно
больше или равно  , то относительно него поступают согласно п. 1 или п. 2. Частное
, то относительно него поступают согласно п. 1 или п. 2. Частное  записывают после
записывают после  ;
;
е) если полученное число  меньше
меньше  , то приписывают еще столько следующих разрядов, сколько необходимо, чтобы получить первое число
, то приписывают еще столько следующих разрядов, сколько необходимо, чтобы получить первое число  , большее или равное
, большее или равное  . В этом случае записывают после
. В этом случае записывают после  то же число нулей. Затем относительно d3 поступают согласно пп. 1, 2. Частное
то же число нулей. Затем относительно d3 поступают согласно пп. 1, 2. Частное  записывают после нулей. Если при использовании младшего разряда числа
записывают после нулей. Если при использовании младшего разряда числа  окажется, что
окажется, что  , то тогда частное чисел
, то тогда частное чисел  и
и  равно нулю, и этот нуль записывается последним разрядом в частном, а остаток
равно нулю, и этот нуль записывается последним разрядом в частном, а остаток  .
.
Приложение 2
