Тема 6. Запись целых неотрицательных чисел и алгоритмы действий над ними
Теоретический материал
Система счисления – язык для наименования, записи чисел и выполнения действий над ними.
Десятичная система счисления
Запись числа в десятичной системе счисления
Десятичная запись числа:
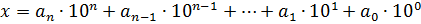
Краткая форма:
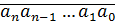
Сумма разрядных слагаемых (начальная школа)
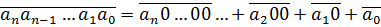
Позиционные системы счисления, отличные от десятичной
Записью натурального числа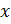 
в системе счисления с основанием p называют его представление в виде: 
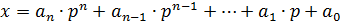, где коэффициенты 
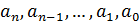принимают значения 
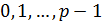и 
.
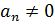Перевод чисел из произвольной системы счисления в десятичную
Пусть дана запись числа x в системе счисления с основанием p, т.е. 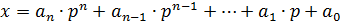. Так как в записи чис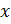ла числа 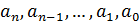и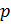 
представлены в десятичной системе счисления, то выполнив над ними действия по правилам, принятым в ней, получим десятичную запись числа .
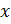Перевод чисел из десятичной системы счисления в произвольную
Запись числа 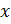в 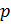-ичной системе находят так: число 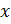делят (в десятичной системе) на p; остаток, полученный при делении, даст последнюю цифру 
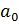в 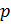-ичной записи числа 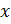; неполное частное снова делим на 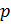, новый остаток даст предпоследнюю цифру 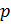-ичной записи числа 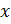; продолжая деление, найдем все цифры p-ичной записи числа .
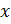1. Запишите число в виде десятичной записи (1) и в виде суммы разрядных слагаемых (2):
2. Замените следующие суммы краткой записью числа:
1)  | |
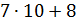2)  | |
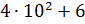3)  | |
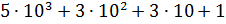4)  | |
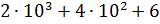5)  | |
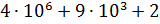6)  |
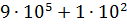3. Разность между наибольшим трехзначным числом и задуманным в 2 раза больше разности между задуманным числом и наибольшим двузначным числом. Найдите задуманное число. [3, с. 130]
4. Существует ли трехзначное число, в котором число десятков на 4 меньше числа единиц, но на 4 больше числа сотен? Если да, найдите это число.
5. Сумма цифр двузначного числа равна 16. Если из этого числа вычесть число, записанное теми же цифрами, но взятыми в обратном порядке, то получится 18. Найти это число.
6. Запишите наибольшее трехзначное число, в записи которого все цифры различные.
7. Сколько разрядов будет содержать наибольшее число, в котором все цифры различны? Запишите это число и представьте его в виде десятичной записи числа и суммы разрядных слагаемых.
8. Составьте два натуральных числа так, чтобы их произведение было наибольшим, при этом цифры, используемые для записи обоих чисел, не должны повторяться. [3, с. 130]
9. Найдите четырехзначное число, если сумма цифр в записи этого числа равна 24, а каждая последующая цифра (начиная с единиц) меньше предыдущей на 2. [3, 130]
10. Составьте таблицу сложения однозначных чисел в десятичной системе счисления в следующей форме:
11. Составьте таблицу сложения однозначных чисел в десятичной системе счисления в следующей форме:
12. Вычислите значения выражений, представив числа в развернутой форме:
а) 11+93+429+317;
б) 23+248+227+32;
в) 326+758+374;
г) 684+353+647;
д) 3567 – (1267 – 789);
е) 15395 – (4375 – 1297);
ж) (3128 + 7289) – (1028 + 5285);
з) 78589 – (58384 + 17108).
13. Выполните сложение столбиком:
а) 3170 + 9735;
б) 543290 + 37826;
в) 68730 + 659100;
г) 673545 + 775367.
14. Выполните вычитание столбиком:
а) 3567 – 1209;
б) 15395 – 4107;
в) 74538 – 3229;
г) 989465 – 778156.
15. На примере умножения следующих чисел проиллюстрируйте теоретические основы алгоритма умножения многозначного числа на однозначное:
а)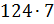 
;
б)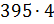 
;
в)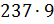 
.
16. Выполните умножение столбиком, объясняя каждый шаг алгоритма
а)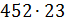 
;
б)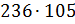 
;
в)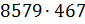 
;
г)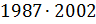 
.
17. Выполните деление уголком, объясняя каждый шаг алгоритма:
а)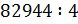 
;
б)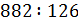 
;
в)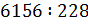 
;
г)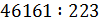 
;
д)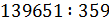 
.
18. Перейдите от краткой записи числа к развернутой:
а)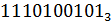 
;
б)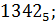 
в)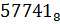 
.
19. Запишите числа 138, 2523, 32456 в двоичной, восьмеричной и шестнадцатеричной системах счисления:
| Система счисления | |||
| Двоичная | |||
| Восьмеричная | |||
| Шестнадцатеричная |
Решение:
20. Перевести числа в десятичную систему счисления:
| Исходные числа | Числа в десятичной системе |
 | |
 | |
 | |
 | |
 | |
 | |
 |
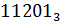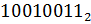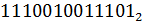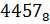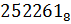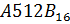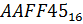Решение:
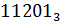
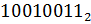
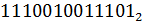
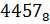
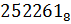
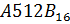
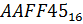
21. Составьте таблицу сложения однозначных чисел в восьмеричной системе счисления:
22. Составьте таблицу умножения однозначных чисел в восьмеричной системе счисления: