Получение математических моделей в приложениях Mathcad и Excel

В приложении Mathcadможно записать формулы приведенного выше алгоритма и вычислить коэффициенты функциональной зависимости.

Существуют также и встроенные функции для определения математических моделей. Например, пусть имеются значения х и у, полученные в результате проведения опытов. Надо найти математическую модель в виде полинома второй степени:

y = a0 + a1 × x + a2 × x²

Можно использовать для решения задачи встроенную функцию linfit. На листе Mathcadтогда нужно записать:

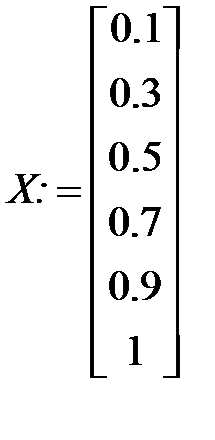
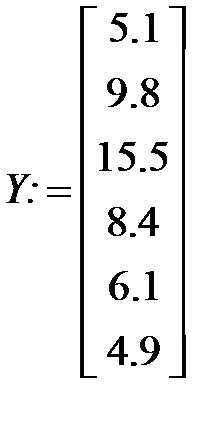
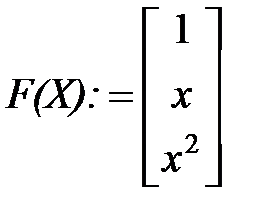
А:= linfit(Х, Y, F)

Вычисленные значения a0, a1, a2будут записаны в векторе А, который появится после ввода текста: A =

Для построения графика теперь можно определить значения:

i :=0..5 t := 0, 0.01..1 Z(t) := F(t)*A

Здесь Z(t) − искомая математическая модель. Если построить на одном графике зависимость Z(t) от t и зависимость Y_i от X_i, то можно сравнить, насколько хорошо полученный полином описывает данные опытов.

В приложении Excel предоставляется интересная возможность получения математических моделей через построение графиков функций.

Пусть имеются значения x₁, x₂, …, x_nи соответствующие им значения y₁, y₂, …, y_n. Надо для этих данных построить точечный график и выполнить команду Диаграмма/Добавить линию тренда. В появившемся окне на вкладке Тип определить вид математической модели, а на вкладке Параметры отметить флажок Показывать уравнение на диаграмме. После нажатия <ОK> искомое уравнение появится на графике.

Модель многомерного объекта

Предположим, что технологический процесс можно описать математической моделью вида

y = b₀ + b₁×x₁ +…+ b_n×x_n + b₁₂×x₁×x₂ +…+ b_n–1,n×x_n–1×x_n,

где y – выходной параметр процесса; b₀, b₁, …, b_n–1,n – искомые неизвестные коэффициенты процесса; x₁, …, x_n – входные параметры процесса.

Соотношения такого вида называются уравнениями регрессии.

Например, для процесса (рис. 21.2), имеющего три входных параметра (фактора), математическая модель примет вид

y = b₀ + b₁ × x₁ + b₂ × x₂ + b₃ × x₃ + b₁₂ × x₁ × x₂ + b₁₃ × x₁ × x₃ + b₂₃ × x₂ × x₃.

Чтобы определить коэффициенты математической модели процесса необходимо провести эксперимент по соответствующему плану, например по плану полного факторного эксперимента.

Рис. 21.2. Многомерный объект

Количество опытов в эксперименте рассчитывается по формуле N = 2ⁿ, где n – количество факторов. Входные воздействия принимают минимальные и максимальные значения. Для упрощения вычислений нужно перейти от физических переменных x₁, …, x_n к кодированным по следующей формуле:

z_i = 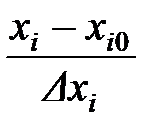,i = 1, 2, 3.

Здесь x_i0 – значение фактора на базовом (нулевом) уровне, равное среднему значению между минимальным и максимальным значениями; ∆x_i – интервал варьирования по данному фактору.

В случае трех входных параметров план проведения эксперимента имеет вид, представленный на рис. 21.3.

№ п/п z1 z2 z3 уэ –1 –1 –1 уэ1 +1 –1 –1 уэ2 –1 +1 –1 уэ3 +1 +1 –1 уэ4 –1 –1 +1 уэ5 +1 –1 +1 уэ6 –1 +1 +1 уэ7 +1 +1 +1 уэ8

Значение –1 соответствует минимальному значению входного параметра, +1 – максимальному значению входного параметра.

В соответствии с методом наименьших квадратов производится вычисление коэффициентов:

Рис. 10.3. План эксперимента

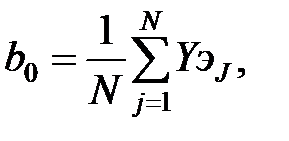
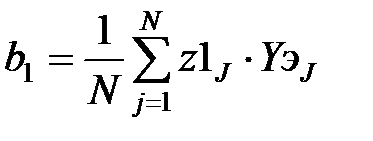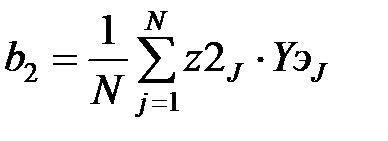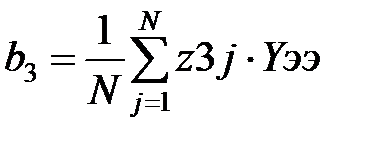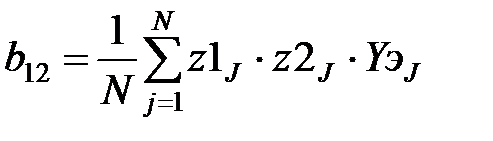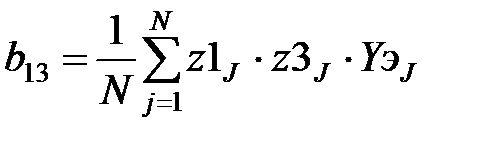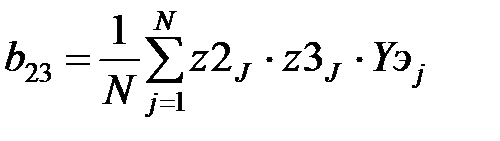, , , , , , i=1,2,…,N

Коэффициент регрессии b (b₀, b₁, …, b_n–1,n.) считается значимым, если выполняется условие

, ,

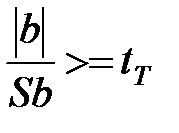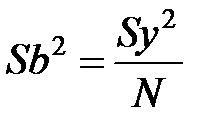где Sb – среднеквадратичная ошибка в определении коэффициентов регрессии; t_Т– табличное значение критерия Стьюдента, которое выбирается для числа степеней свободы f1 = m – 1.

Для расчета дисперсии воспроизводимости нужно выполнить дополнительно m опытов (m < N) по любой строчке плана, например, при значениях входных факторов на базовом уровне.

В результате получаются дополнительные значения экспериментальных данных yd₁,yd₂, …, yd_m.

Тогда

Sy² = 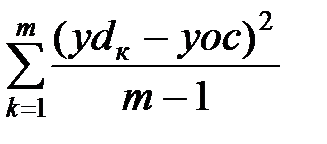, yoc =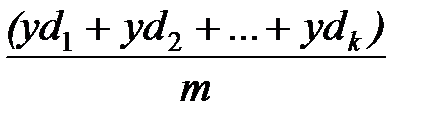, k=1, …, m.

В табл. 10.1 приведены значения критерия Стьюдента.

Таблица 10.1

Значения критерия Стьюдента

Число степеней свободы f1
Значение коэффициента	12.71	4.30	3.18	2.78	2.57	2.45	2.36

Если коэффициент не удовлетворяет критерию Стьюдента, то он считается незначимым и приравнивается к нулю.

Проверка адекватности (соответствия) полученного уравнения регрессии экспериментальным данным проводится с помощью критерия Фишера. Для этого вычисляются

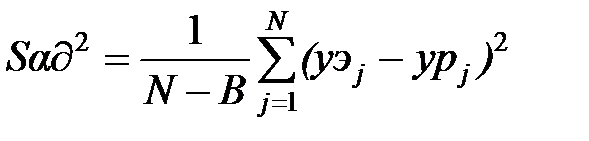, F = ,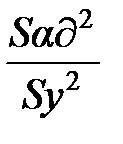

где 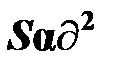– оценка дисперсии адекватности; B – число значимых коэффициентов уравнения регрессии; yэ_j, yp_j – экспериментальное и рассчитанное по найденной математической модели значения y в j-м опыте.

Определяется также табличное значение критерия Фишера F_Т из табл. 21.2 по числу степеней свободы f1 и числу степеней свободы f2 = N – B.

Если F < F_Т, то уравнение регрессии рассматривается как модель исследуемого процесса.

Таблица 10.2