Технология построения эпюр внутренних силовых факторов на пространственных стержневых конструкциях

Что такое пространственная стержневая конструкция?

Это конструкция, состоящая из связанных стержней, находящихся в разных плоскостях. Например:

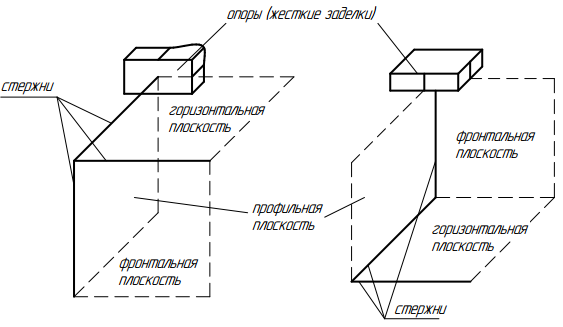
Обе пространственные конструкции консольного типа состоят из трех стержней, связанных между собой в узловых точках под углом в 90º.

Какие внутренние силовые факторы возникают в сечениях элементов пространственной стержневой конструкции?

При нагружении элементов конструкции внешними нагрузками в их поперечных сечениях могут возникнуть шесть внутренних силовых факторов: продольная сила N, поперечные силы Q_х и Q_у, изгибающие моменты M_х и М_у и крутящий момент М_z.

Какие существуют особенности при построении эпюр внутренних силовых факторов на пространственных стержневых конструкциях?

1. Воздействие внешних сил и, соответственно, возникающие от них внутренние силовые факторы на каждом стержне рассматриваются по плоскостям декартовой пространственной системы координат.

2. На каждом стержне используют локальную систему координат: ось z совмещают с продольной осью стержня, а оси x и y – горизонтальная и вертикальная оси, соответственно, в поперечном сечении стержня. Например:

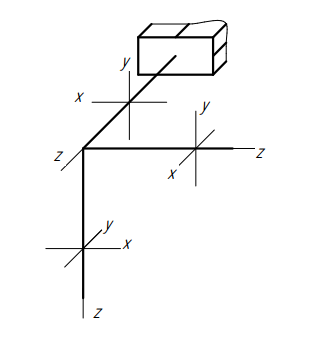
3. Силы, удаленные от рассматриваемого стержня, но находящиеся на рассматриваемой части конструкции, рекомендуется приводить к началу данного стержня по правилам переноса сил и включать в число внешних сил, воздействующих на данный стержень.

4. Эпюры следующих внутренних силовых факторов рекомендуется строить на одной базе:

· поперечные силы Q_x и Q_y, ординаты которых откладывают по осям х и y, соответственно;

· изгибающие моменты M_x и M_y, ординаты которых откладывают в сторону сжатых волокон в двух взаимно перпендикулярных плоскостях (плоскостях изгиба).

В остальном, все закономерности и приемы построения эпюр внутренних силовых факторов, рассмотренные на стержнях, балках и плоских рамах, применяются также на пространственных стержневых конструкциях.

1.5.2. Пример решения задачи

Задача

Для данной консольной пространственной стержневой конструкции построить эпюры внутренних силовых факторов.

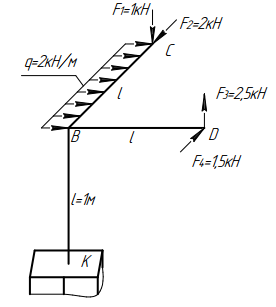
РЕШЕНИЕ

Перед началом решения задачи напоминаем :

1. База эпюры представляет собой геометрическую конфигурацию расчетной схемы без опорных элементов и внешних нагрузок.

2. Построение каждой эпюры для консольной конструкции начинаем со свободных концов, двигаясь через узловые точки к заделке.

3. При построении эпюр применяем метод построения по характерным сечениям с использованием основных закономерностей для каждого внутреннего силового фактора.

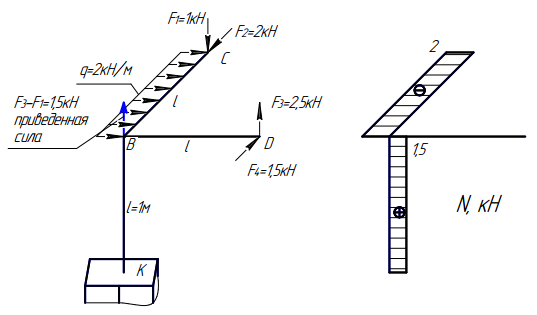
Построение эпюры продольной силы N

Участок СВ. Анализ состояния в начале участка: на свободном конце участка CB в т. «С» находится сила F₂=2кН, действующая по продольной оси стержня и производящая деформацию сжатия. От ее действия откладываем от базы скачок на величину -2кН в любой удобной для этого плоскости (горизонтальной или профильной). Мы отложили ординату -2кН в горизонтальной плоскости, приняв отрицательные значения слева от базы. Анализируем состояние по длине участка: при движении от свободного конца к узлу в т. «В» нет больше сил, действующих вдоль или параллельно продольной оси участка СВ. Поэтому проводим прямую, параллельную базе, ординатой ‑2кН до конца участка.

Участок DB. Анализ состояния в начале участка: на свободном конце участка отсутствует сила, действующая по продольной оси стержня, поэтому на эпюре будет 0. Анализируем состояние по длине участка: он пустой, ничем не загружен, т.е. по всей длине стержня продольная сила также будет отсутствовать.

Участок ВK. Анализ состояния в начале участка: для этого необходимо в точку «В» привести все силы, параллельные продольной оси стержня BK, со стержней «СВ» и «DB». Это силы F₁=1кН и F₃=2,5кН. Т.к. они имеют разное направление, то их суммарный вектор равен F₃-F₁=1,5кН и имеет направление силы F₃, т.е. вверх, и оказывает растягивающее воздействие на стержень «BK». На эпюре эта приведенная сила даст скачок величиной 1,5кН, который откладываем также в любой визуально удобной для этого плоскости: фронтальной или профильной. Мы отложили во фронтальной плоскости, приняв положительные значения справа от базы. Анализируем состояние по длине участка: он пустой, т.е. проводим прямую, параллельную базе, до конца участка ординатой 1,5кН.

Построение эпюры поперечных сил Q_x и Q_y

Участок СВ.

Эпюра поперечной силы Q_у. Анализ состояния в начале участка: в начале участка на свободном конце находится сосредоточенная сила F₁=1кН, дающая проекцию на ось у поперечного сечения участка. Это вызовет скачок на эпюре Q_y, равный величине силы. Знак скачка определим, поворачивая силу F₁ по направлению движения по участку (от т. «С» к т. «В»). Сила поворачивается по часовой стрелке, т.е. знак поперечной силы «+». Откладываем от базы ординату =1кН по оси у (вертикальной оси) вверх, приняв положительные значения выше базы. Анализ состояния по длине участка: т.к. больше нет внешних нагрузок, дающих проекцию на вертикальную ось у поперечных сечений стержня, то проводим прямую, параллельную базе, ординатой 1кН до конца участка.

Эпюра поперечной силы Q_x Анализ состояния в начале участка: сосредоточенных сил, дающих проекцию на ось х поперечного сечения в начале участка в т. «С» нет. Поэтому эпюру Q_x начинаем с 0. Анализируя состояние по длине участка, видим, что участок закружен в горизонтальной плоскости равномерно распределенной нагрузкой, которая проецируется на ось х поперечных сечений. Это означает, что от нуля в начале участка надо провести наклонную прямую с угловым коэффициентом q=2кН/м. Для построения наклонной прямой определим значение Q_x в конце участка в т. «В», умножив интенсивность нагрузки на длину участка: 2кН/м×1м=2кН. Знак поперечной силы Q_x определим, поворачивая стрелки нагрузки по направлению движения по участку (от т. «С» к т. «В»). Поворот происходит по часовой стрелке, значит знак Q_x «+». Откладываем в т. «В» участка CB от базы по оси х влево ординату 2кН, приняв положительные значения с левой стороны, и соединяем с 0 в т. «С».

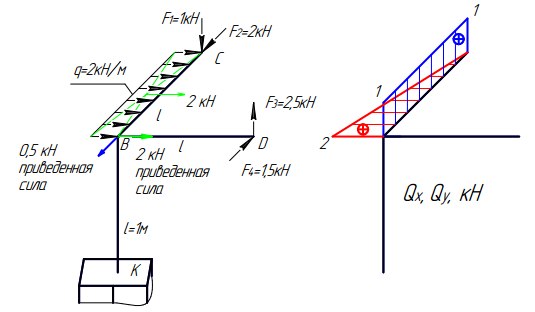
Участок DB. Анализ состояния в начале участка: в начале участка в т. D находятся две сосредоточенные силы:

· F₃=2,5кН, которая дает проекцию на ось у поперечного сечения и вызовет скачок на эпюре Q_y, равный -2,5кН, т.к. сила поворачивается по направлению движения по участку от т. «D» к т. «В» против часовой стрелки.

· F₄=1,5кН, которая дает проекцию на ось х поперечного сечения и вызовет скачок на эпюре Q_x =-1,5кН, т.к. сила тоже поворачивается против часовой стрелки по направлению движения по участку.

Откладываем соответствующие ординаты в т. «D» от базы по осям у и х -2,5кН вниз во фронтальной плоскости и -1,5кН вправо в горизонтальной плоскости. Анализ состояния по длине участка: участок ничем не загружен ни в горизонтальной, ни во фронтальной плоскости. Поэтому в горизонтальной и фронтальной плоскостях проводим прямые, параллельные базе, величиной соответствующих ординат.

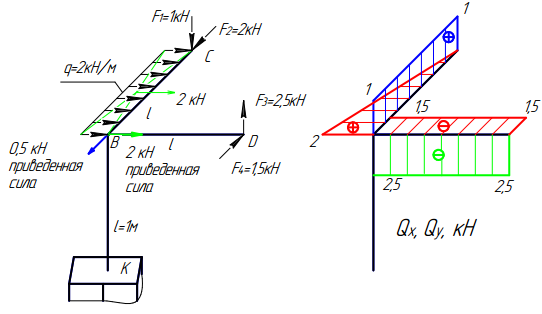
Участок BK. Сначала приведем в точку «B» все силы с участков CB и DB, дающие проекции на оси х и у. Это равнодействующая распределенной нагрузки 2qℓ=2кН, дающая проекцию на ось х поперечного сечения, и суммарный вектор сил F₂ и F₄, равный 0,5кН и направленный в сторону большей силы F₂, дающий проекцию на ось у поперечного сечения. Эти приведенные силы вызывают скачки в точке «В»: на эпюре Q_x=2кН и на эпюре Q_y=-0,5кН. Знак скачков определяем по той же технологии, поворачивая приведенные силы по направлению построения эпюр, от т. «В» к т. «K». Приведенная горизонтальная сила 2кН поворачивается по часовой стрелке, что говорит о положительном знаке Q_x. А приведенная сила в 0,5кН поворачивается против часовой стрелки, что определяет отрицательный знак скачка на эпюре Q_y. Анализ состояния по длине участка: участок ничем не загружен. Это означает, что на эпюрах Q_x и Q_y будут прямые, параллельные базе, которые проводим в профильной плоскости ординатой -0,5кН, а во фронтальной – ординатой 2кН.

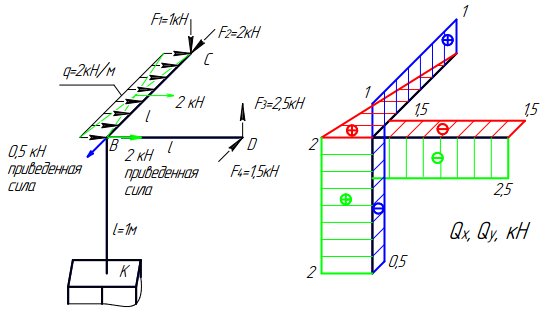
Построение эпюры изгибающих моментов M_x и М_у

Участок CB. Изгиб этого стержня возможен в двух плоскостях: горизонтальной и профильной. Момент М_х возникает в профильной плоскости, а М_у в горизонтальной.

Эпюра М_х в профильной плоскости: в начале участка на свободном конце стержня в т. «С» отсутствует сосредоточенный внешний момент, поэтому эпюру начинаем с 0. Анализ состояния по длине участка: участок пустой, т.е. должна быть наклонная прямая с угловым коэффициентом, равным Q_y этого участка. Для ее построения определим значение М_х в конце участка в т. «В» по части «СВ». Момент создает сила F₁=1кН с плечом ℓ=1м, т.е. М_х=F₁×ℓ=1кНм. Откладываем эту величину в т. «В» на нижние сжатые волокна по направлению момента от F₁ и соединяем с 0 в т. «С».

Эпюра М_у в горизонтальной плоскости: в начале участка в т. «С» отсутствует сосредоточенный внешний момент, поэтому эпюру М_у начинаем с нуля. Анализ состояния по длине участка: участок загружен в горизонтальной плоскости равномерно распределенной нагрузкой, поэтому должна быть парабола, выпуклость которой – навстречу направлению нагрузки. Вероятность наличия экстремума проверяем по эпюре Q_x на данном участке. Наклонная прямая на эпюре Q_x не пересекает базу, значит, парабола будет без экстремума. Такие параболы строят по двум точкам. Для этого определим значение М_у в конце участка в т. «В» по части «СВ» от распределенной нагрузки, заменяя ее равнодействующей, равной 2кН (вектор зеленого цвета на рис.), которую помещаем в точку центра тяжести площади, занимаемой нагрузкой. Расстояние от равнодействующей до т. «В» – 0,5 метра, тогда величина М_у=2кН×0,5м=1кНм. Откладываем эту величину в т. «В» по направлению действия момента от распределенной нагрузки на правые сжатые волокна в горизонтальной плоскости и соединяем с нулем параболой, выпуклость которой направляем вправо, навстречу вектору q.

Таким образом, на стержне CB мы получили эпюры M_x и М_у в виде двух плоских фигур: линейного треугольника (синего цвета) и параболического треугольника (красного цвета), которые находятся в профильной и горизонтальной плоскости, соответственно.

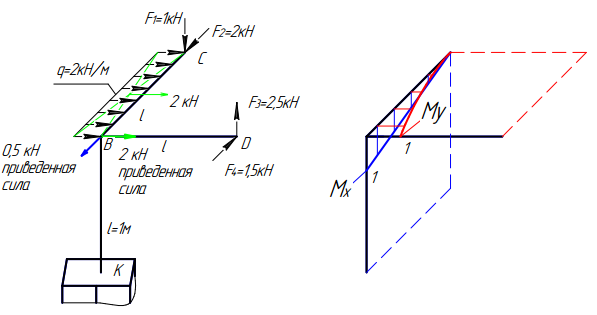
Участок DB. Изгиб данного участка может происходить в горизонтальной и фронтальной плоскостях. В горизонтальной плоскости будет возникать изгибающий момент М_у, а во фронтальной – М_х.

Эпюра М_х во фронтальной плоскости. Анализ состояния в начале участка: на свободном конце в т. «D» отсутствует сосредоточенный внешний момент, т.е. начинаем построение эпюры с 0. Анализ состояния по длине участка: участок ничем не загружен, т.е. должна быть наклонная прямая с угловым коэффициентом, равным Q_y данного участка. Для построения наклонной прямой определим значение М_х в конце участка в т. «В» по части DB. Момент будет создавать сила F₃=2,5кН с плечом 1м: М_х=2,5кН×1м=2,5кНм. Откладываем это значение в т. «В» на верхние сжатые волокна по направлению действия момента от силы F₃ и соединяем с нулем в т. «D».

Эпюра М_у в горизонтальной плоскости. Анализ состояния в начале участка: на свободном конце в т. «D» отсутствует сосредоточенный внешний момент, т.е. начинаем построение эпюры с 0. Анализ состояния по длине участка: участок ничем не загружен, т.е. должна быть наклонная прямая с угловым коэффициентом Q_х данного участка. Для построения наклонной прямой определим значение М_у в конце участка в т. «В» по части DB. Момент будет создавать сила F₄=1,5кН с плечом 1м: М_у=1,5кН×1м=1,5кНм. Откладываем это значение в т. «В» на правые сжатые волокна по направлению действия момента от силы F₄ и соединяем с нулем в т. «D». Таким образом, на стержне DB мы получили эпюры M_x и М_у в виде двух плоских фигур – линейных треугольников, которые находятся во фронтальной и горизонтальной плоскости, зеленого и красного цвета соответственно.

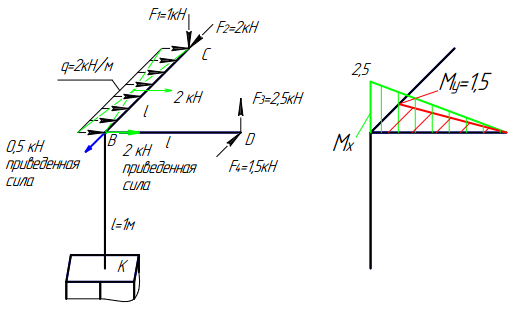
Участок BK. Изгиб данного участка может происходить во фронтальной и профильной плоскостях. В профильной плоскости будет возникать изгибающий момент М_х, а во фронтальной – М_у. В горизонтальной плоскости данный участок может подвергаться деформации кручения, что сопровождается возникновением внутреннего крутящего момента М_z.

Эпюра М_х в профильной плоскости. Анализ состояния в начале участка в т. «В». В профильной плоскости в данную точку приведен момент с участка CB, равный 1кНм, который передаем на участок BK по направлению действия данного момента, т.е. на правые сжатые волокна стержня в профильной плоскости. Анализ состояния по длине участка: участок ничем не загружен, т.е. должна быть наклонная прямая с угловым коэффициентом Q_y=-0,5кН. Для построения наклонной прямой определим значение М_х в конце участка в т. «K». Направление приведенной в т. «В» силы 0,5кН (синий вектор на рисунке) показывает направление изменения момента М_х с правых сжатых волокон в профильной плоскости на левые волокна. В пределах длины участка (1 метр) это изменение произойдет на величину 0,5кН×1м=0,5кНм. Вычисление момента М_х в точке «K» сделаем в табличном виде:

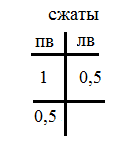
Здесь в таблице: пв – правые волокна, лв – левые волокна. Таким образом, отложив 0,5кНм на правые сжатые волокна в т. «K» в профильной плоскости и соединив с ординатой 1кНм в начале участка, получим трапецию (на рисунке синего цвета).

Эпюра М_у во фронтальной плоскости. Анализ состояния в начале участка в т. «В»: во фронтальной плоскости в данную точку приведен момент с участка DB, равный 2,5кНм (на рисунке зеленого цвета), который передаем на левые сжатые волокна стержня ВК по направлению действия момента. Анализ состояния по длине участка: участок ничем не загружен. Значит, должна быть наклонная прямая с угловым коэффициентом, равным Q_x=2кН данного участка. Направление изменения момента М_у от величины 2,5кНм в начале участка определим по направлению вектора приведенной в т. «В» силы, равной 2кН (на рисунке зеленого цвета), которое указывает на изменение момента с левых сжатых волокон на правые на величину, равную 2кН×1м=2кНм. Вычислим значение М_у в конце участка BK в табличной форме:

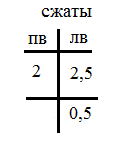
Отложив величину ординаты равную 0,5кНм в конце участка во фронтальной плоскости на левые сжатые волокна участка «BK» и соединив с величиной 2,5кНм, получим трапецию (на рисунке зеленого цвета).

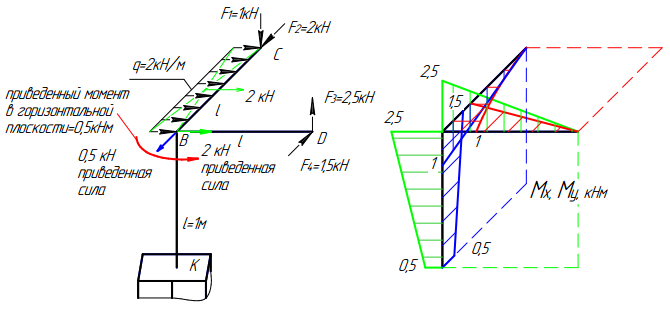
Эпюра крутящего момента М_z в горизонтальной плоскости. Анализ состояния в начале участка в т. «В»: в горизонтальной плоскости приведено два момента: с участка CB 1кНм и с участка DB 1,5кНм (на рисунке красные ординаты). Сначала алгебраически складываем эти моменты, учитывая направления их действия: момент, равный 1кНм, действует по часовой стрелке (согласно направлению действия равнодействующей распределенной нагрузки), а момент, равный 1,5кНм, – против часовой стрелки (согласно направлению действия силы F₄). Результирующий момент равен: 1,5-1=0,5кНм и имеет направление против часовой стрелки (на расчетной схеме красного цвета). Откладываем его на базе участка «ВК» в т. «В» в любой, удобной для визуального восприятия, плоскости. Мы отложили эту ординату на эпюре во фронтальной плоскости. Анализ состояния по длине участка: участок ничем не загружен. Согласно закономерностям при построении эпюры крутящего момента это означает, что на всем участке крутящий момент не изменяется и равен 0,5кНм. На эпюре это будет прямоугольник ординатой 0,5кНм.

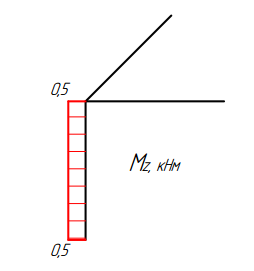
Эпюры построены!

1.5.3. Задача для самостоятельного решения на занятии

Для заданной расчетной схемы построить эпюры внутренних силовых факторов, используя метод построения по характерным сечениям.

1.5.4. Потренируемся?

· Пройти тестовый тренинг (Приложение 2, тесты к ПЗ №4, стр. 212)

· Решить задачу 1.5. из РПР№1 (Приложение 4, стр. 271)

Модуль №2
Напряжения и деформации при растяжении-сжатии. Механические испытания материалов при растяжении-сжатии. Расчет на прочность и жесткость при растяжении-сжатии

Цель занятий в модуле:

Освоить методику проведения испытаний материала при растяжении-сжатии. Научиться перестраивать машинную диаграмму испытания при растяжении в условную диаграмму и определять основные механические характеристики материала, используя результаты испытания. Научиться рассчитывать стержневые конструкции, работающие в условиях растяжения-сжатия, на прочность и жесткость.

Необходимые знания для достижения цели:

1. Типы образцов, используемые для испытания на растяжение, и методика проведения испытания на растяжение.

2. Машинная и условная диаграммы испытания.

3. Основные механические характеристики, определяемые по результатам испытания на растяжение.

4. Алгоритм перестроения машинной диаграммы испытания на растяжение в диаграмму условную.

5. Условие прочности по допускаемому напряжению при растяжении-сжатии.

6. Алгоритм расчета на прочность.

7. Задачи, вытекающие из условия прочности.

8. Условие жесткости при растяжении-сжатии по величине допускаемого перемещения.

9. Алгоритм расчета на жесткость.