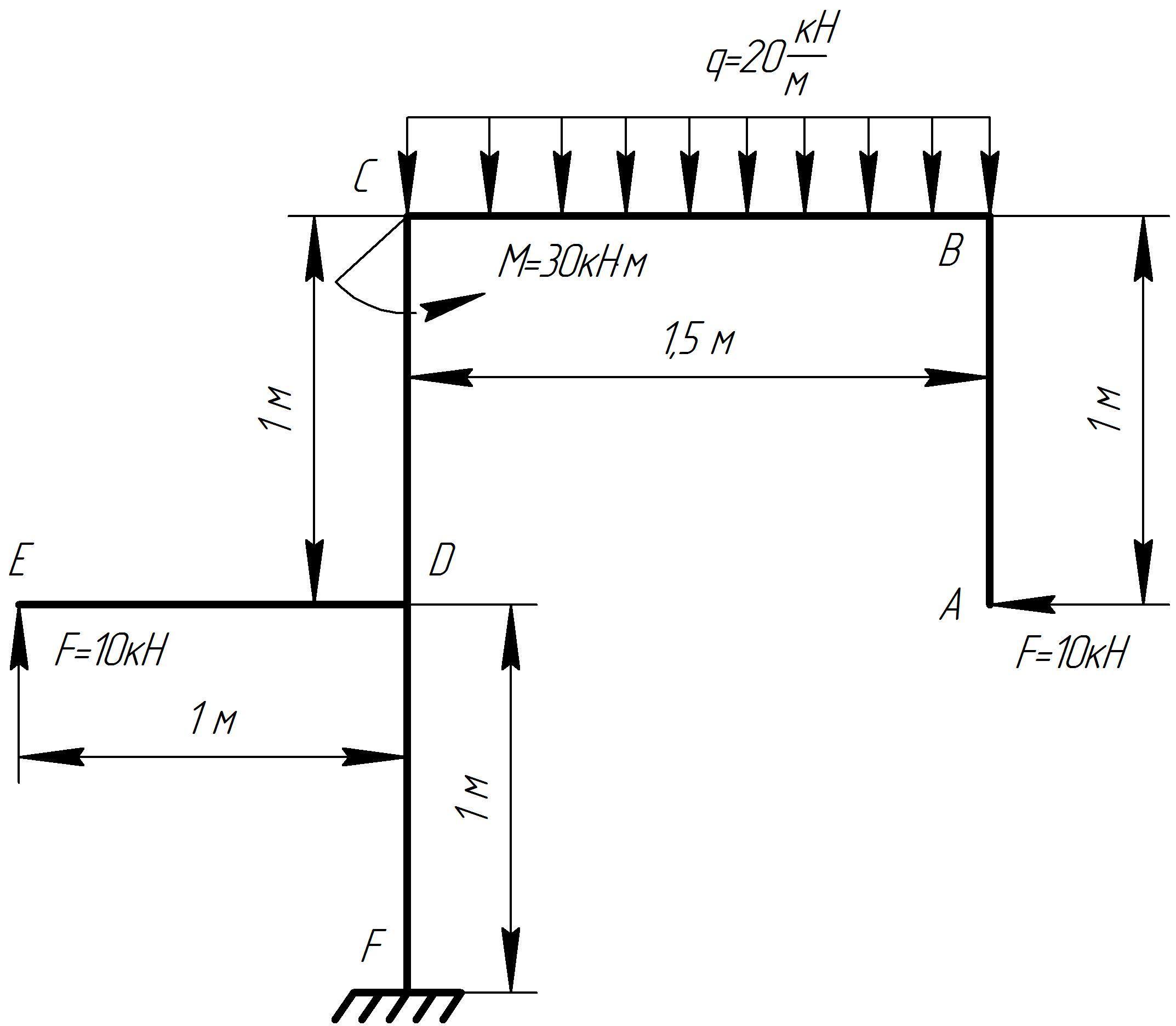
Часть 1. Построение эпюр внутренних силовых факторов на консольной раме
 Какие существуют особенности построения эпюр внутренних силовых факторов на консольных рамах?
Какие существуют особенности построения эпюр внутренних силовых факторов на консольных рамах?
При построении эпюр на консольных рамах так же, как и на консольных балках, используют возможность не определять реактивных усилий в заделке. При этом принимают строго определенное направление построения эпюр от свободного конца (концов) к заделке.
1.4.3.  Пример решения задачи
Пример решения задачи
Задача
Построить эпюры внутренних силовых факторов на данной консольной раме.
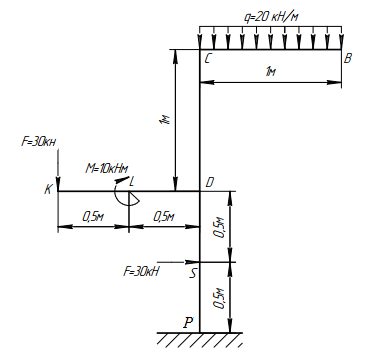
РЕШЕНИЕ
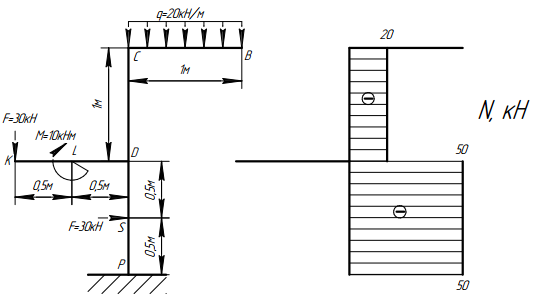
Построение эпюры продольной силы N
Выберем направление построения эпюры N. Т.к. рама консольного типа, строить эпюру будем, идя со свободных концов ригелей «ВС» и «KD» сначала к узлу «D», а затем от узла к заделке, не определяя реактивных сил.
1. Верхний ригель ВС. Движемся от точки «В» к точке «С». В начале участка в т. «В» отсутствует внешняя сила, способная дать проекцию на продольную ось участка, т.е. начинаем с нуля. Далее по длине участка действует равномерно распределенная нагрузка, которая также не дает проекцию на продольную ось. Таким образом, продольная сила на участке «ВС» равна 0.
2. Верхняя часть стойки CD. Движемся от точки «С» к точке «D», рассматривая стойку вместе с верхним ригелем. В точке «С» на продольную ось стойки дает проекцию равнодействующая распределенной нагрузки, равная q×1м=20кН. Т.к. распределенная нагрузка оказывает сжимающее воздействие на стойку «CD», в т. «C» стойки откладываем скачок относительно вертикальной базы стойки на величину 20кН (на эпюре принято отрицательное направление справа от базы). Т.к. участок «CD» пустой, проводим прямую, параллельную базе, до конца участка, т.е. до т. «D».
3. Левый ригель KD. Движемся от точки «K» к точке «D». В начале участка в т. «K» отсутствует сила, способная дать проекцию на продольную ось ригеля, начинаем эпюру N с 0. Т.к. сосредоточенный момент, находящийся в т. «L», не оказывает влияния на продольную силу, и оба участка ригеля «KL» и «LD» пустые, то далее можно сделать вывод об отсутствии продольной силы на всем ригеле.
4. Нижняя часть стойки DP. Движемся от точки «D» к точке «Р», рассматривая влияние всех сил, находящихся на обоих ригелях и верхней части стойки. В начале участка «DP» в точке «D» видим, что на продольную ось участка дает проекцию как равнодействующая распределенной нагрузки, так и сила F=30кН, находящаяся в точке «K» левого ригеля. Она также производит сжимающее воздействие на нижнюю часть стойки, поэтому вызовет скачок на эпюре N на 30кН в отрицательную сторону. Получим ординату, равную ‑50кН. Сосредоточенная сила F=30кН, находящаяся в точке «S», не дает проекции на продольную ось стойки, поэтому, игнорируя эту силу, проведем прямую, параллельную базе, величиной ординаты -50кН до конца участка.
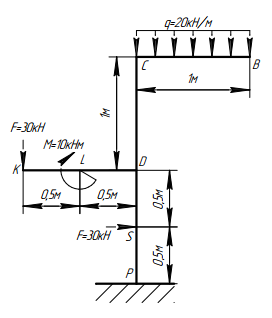
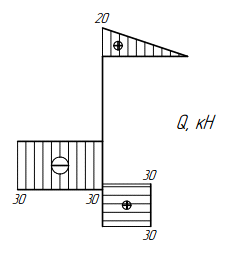
Построение эпюры поперечной силы Q
1. Верхний ригель ВС. Движемся от точки «В» к точке «С». В начале участка в т. «В» отсутствует внешняя сосредоточенная сила, способная дать проекцию на вертикальную ось поперечного сечения, т.е. начинаем с нуля. Далее по длине участка действует равномерно распределенная нагрузка, которая проецируется на вертикальную ось поперечного сечения и на эпюре Q дает наклонную прямую. Знак на эпюре Q определяем путем поворота стрелок интенсивности нагрузки по ходу движения по участку. Поворот происходит по часовой стрелке, т.е. распределенная нагрузка создает положительную поперечную силу. На длине участка в 1 метр распределенная нагрузка имеет равнодействующую, равную 20кН. Это значение откладываем в конце участка в т. «С» вверх, соединяя с нулем в начале участка.
2. Верхняя часть стойки CD. Движемся от точки «С» к точке «D», рассматривая стойку вместе с верхним ригелем. В точке «C» стойки отсутствует внешняя сосредоточенная сила, дающая проекцию на ось поперечного сечения, т.е. начинаем с 0. Т.к. участок «CD» пустой, то можно сказать, что на всем участке поперечная сила будет равна 0.
3. Левый ригель KD. Движемся от точки «K» к точке «D». В начале участка в т. «K» находится сосредоточенная сила F=30кН, способная дать проекцию на ось поперечного сечения ригеля. Она вызывает скачок на эпюре Q. Знак скачка определяем, поворачивая силу по ходу движения по ригелю. Поворот сила делает против часовой стрелки, т.е. откладываем в точке «K» величину -30кН. Т.к. сосредоточенный момент, находящийся в т. «L», не оказывает влияния на поперечную силу, два участка ригеля «KL» и «LD» пустые, то далее проводим прямую, параллельную базе, ординатой -30кН до конца участка.
4. Нижняя часть стойки DP. Движемся от точки «D» к точке «Р», рассматривая влияние всех сил, находящихся на обоих ригелях и верхней части стойки. В начале участка «DP» в точке «D» видим, что нет сил, которые могли бы дать проекцию на ось поперечного сечения. В пределах незагруженного участка «DS» поперечная сила равна 0. В точке «S» находится сосредоточенная сила F=30кН, которая дает проекцию на ось поперечного сечения и вызовет скачок на эпюре «Q». Знак скачка определим, поворачивая силу по ходу движения от точки «S» к точке «Р». Она поворачивается по часовой стрелке, т.е. откладываем от вертикальной базы стойки в точке «S» величину ординаты +30кН. Т.к. участок «SP» ничем не загружен, проводим прямую, параллельную базе, величиной ординаты +30кН до конца участка.
Построение эпюры изгибающего момента М
1. Верхний ригель ВС. Движемся от точки «В» к точке «С». В начале участка в т. «В» отсутствует внешний сосредоточенный изгибающий момент, способный дать скачок на эпюре момента, т.е. начинаем с нуля. Далее по длине участка действует равномерно распределенная нагрузка, которая на эпюре М дает квадратичную параболу, выпуклость которой направлена навстречу действию нагрузки. Т.к. на эпюре Q данного участка наклонная прямая не пересекает базу, квадратичная парабола будет без экстремума. Такие параболы можно строить по двум точкам. Поэтому определим величину внутреннего изгибающего момента в сечении «С» по части «ВС». Момент Мс будет равен моменту от равномерно распределенной нагрузки, т.е. q×1м×0,5м=10кНм. Эту ординату откладываем в точке «С» на нижние сжатые волокна и соединяем с нулем в т. «B» безэкстремальной параболой выпуклостью вверх. Т.к. точка «С» является узловой, передадим ординату момента 10кНм в данной точке на верхнюю часть стойки «CD» по направлению момента от q, т.е. на правые волокна стойки.
2. Верхняя часть стойки CD. Движемся от точки «С» к точке «D», начиная с ординаты 10кНм на правых волокнах, полученной с верхнего ригеля. Т.к. поперечная сила Q на участке «CD» равна нулю, то соответственно дифференциальной зависимости 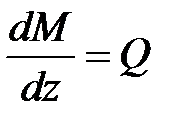 изгибающий момент будет константой, т.е. будет оставаться величиной 10кНм по всей длине верхней части стойки. Проводим прямую, параллельную базе, рассматривая стойку вместе с верхним ригелем.
изгибающий момент будет константой, т.е. будет оставаться величиной 10кНм по всей длине верхней части стойки. Проводим прямую, параллельную базе, рассматривая стойку вместе с верхним ригелем.
3. Левый ригель KD. Разбиваем на два участка «KL» и «LD». Движемся от точки «K» к точке «L». В начале участка в т. «K» отсутствует сосредоточенный внешний момент, поэтому начинаем эпюру с 0. Участок пустой, поэтому должна быть наклонная прямая с угловым коэффициентом, равным Q. Вычисляем значение внутреннего момента в точке «L» по части «KL», умножив величину силы F=30кН на плечо 0,5м: 30×0,5=15кНм. Откладываем это значение на нижние сжатые волокна в т. «L». На границе участков «KL» и «LD» находится внешний сосредоточенный момент М=10кНм, на который делаем скачок вверх от величины 15кНм по направлению данного момента. Получаем величину 5кНм на нижних волокнах, от которой вновь должна быть наклонная прямая до конца участка «LD». Значение момента в точке «D» определим по части «KD»: -F×1м+М= ‑30+10=-20кНм, приняв момент от силы F на нижних сжатых волокнах со знаком «–», а на сжатых верхних от действия момента М со знаком «+». Полученную величину -20кНм отложим в точке «D» на нижние сжатые волокна.
4. Нижняя часть стойки DP. Разбиваем на два участка: «DS» и «SP». Начинаем построение эпюры с участка «DS». Т.к. точка «D» – узловая точка, в которой сходятся три стержня: верхняя часть стойки, левый ригель и нижняя часть стойки, начнем с передачи моментов, приведенных в данную точку с верхней части стойки и левого ригеля. Передачу осуществляем на нижнюю часть стойки, исходя из направлений приведенных моментов: 10кНм с верхней части стойки находится на правых сжатых волокнах, момент с левого ригеля 20кНм передается на левые сжатые волокна. Вычитая из большего момента меньший, откладываем 10кНм на левые волокна в т.«D» нижней части стойки. Т.к. участок DS пустой, на эпюре М должна быть прямолинейная зависимость. Величину углового коэффициента определяем по эпюре Q данного участка. Поскольку QDS равна нулю, на эпюре момента будет прямая, параллельная базе. Т.е. ординатой 10кНм на левых волокнах проведем прямую до конца данного участка. В начале следующего участка SP в точке «S» нет сосредоточенного внешнего момента, поэтому значение момента 10кНм не изменится. Участок пустой, что определяет прямолинейный характер зависимости внутреннего момента с угловым коэффициентом, равным поперечной силе данного участка QSP=30кН. Для построения наклонной прямой определим значение момента в точке «Р», рассматривая влияние всех сил, находящихся на обоих ригелях и верхней части стойки. Определение момента проведем, используя табличную форму вычисления и следующие обозначения: лв – левые волокна стойки, пв – правые волокна стойки.
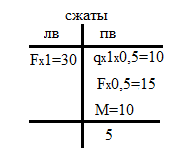
Сложив величины моментов в левом и правом столбцах и вычитая из большего значения меньшее, записываем результат в столбец с большим моментом. Таким образом, в точке «Р» откладываем ординату в 5кНм на правых сжатых волокнах и соединяем с величиной 10кНм в начале участка в точке «S». Получаем наклонную прямую с угловым коэффициентом 30кНм.

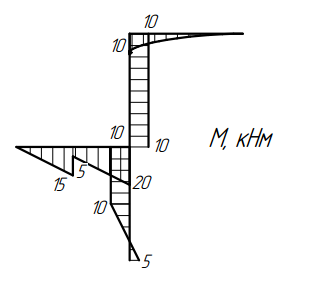
Эпюры построены. 
1.4.4. Задача для самостоятельного решения на занятии
Для данной расчетной схемы рамы построить эпюры внутренних силовых факторов, используя основные закономерности и определяя значения внутренних силовых факторов в характерных сечениях.