Проверка существенности и независимости переменных
Входные переменные подсистем изучаемой производственной системы должны обладать свойствами независимости и существенности.
Свойство независимости состоит в том, что все входные переменные должны быть взаимно независимы либо связь между ними должна быть достаточно слабой, чтобы её можно было игнорировать.
Свойство существенности — в том, что выходная переменная должна зависеть от каждой из входных, причём после получения информации о значениях всех входных переменных энтропия выходной переменной должна быть как можно меньше.
О наличии этих свойств у переменных, включённых в модель, судят на основе статистических показателей тесноты связей, проверки статистических гипотез о независимости переменных, доли энтропии (относительной информативности) переменной, снимаемой информацией о значении другой переменной. Выбирая методы оценки тесноты связи, следует учитывать особенности их содержания. В частности:
¨ критерий χ2 может быть использован применительно к дискретным переменным для проверки гипотез о независимости двух дискретных переменных на основании имеющихся наблюдений (см. Приложение 4), а также о том, не противоречит ли предполагаемая форма связи между переменными имеющимся данным;
¨ однофакторный дисперсионный анализ имеет целью проверку гипотезы о существовании статистически достоверной зависимости непрерывной нормально распределённой переменной[9] от дискретной (или приведённой к дискретной форме) переменной(см. Приложение 5);
¨ метод относительной информативности (см. Приложение 6) позволяет определить, какая доля энтропии одной дискретной переменной снимается другой дискретной переменной. Проверку тесноты связи по этому методу делают после построения таблиц условных вероятностей (см. ниже);
¨ корреляционный анализ оценивает тесноту связи между переменными непрерывными при условии, что связь между ними предполагается линейной. Если величина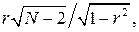 
где N — число наблюдений, а r — коэффициент парной корреляции по Пирсону, оказывается за пределами соответствующего выбранному уровню доверия квантиля распределения Стьюдента для числа степеней свободы N–2, гипотеза о независимости переменных отвергается[10]. Соответствующие вычисления можно выполнить по формуле Excel
=СТЬЮДРАСП(ABS(КоэфКор)/КОРЕНЬ(1-КоэфКор^2)*
КОРЕНЬ(СЧЁТ(Ряд1)-2);СЧЁТ(Ряд1)-2;2).
Здесь КоэфКор — имя ячейки, содержащей коэффициент парной корреляции по Пирсону, вычисляемый по формуле
=ПИРСОН(Ряд1;Ряд2),
Ряд1 и Ряд2 — имена диапазонов ячеек, содержащих наблюдаемые значения переменных, связь между которыми исследуется. В обоих рядах должно быть одинаковое количество ячеек, нечисловых значений и пустых ячеек быть не должно. В программе MathCad соответстствующие вычисления выглядят следующим образом:
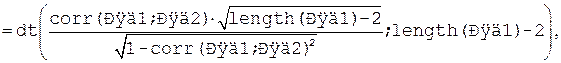
где Ряд1 и Ряд2 — имена векторов, содержащих наблюдения исследуемых переменных.
При исследовании систем принимают во внимание, что независимость некоторой переменной x1от каждой из остальных (x2...xn) ещё не означает, что x1не зависит от некоторой функции f(x2...xn).
Входную (факторную) переменную исключают из модели в следующих случаях:
¨ отсутствие её связи с выходной переменной статистически достоверно;
¨ она тесно коррелирует с другой входной переменной, не исключаемой из модели, либо снимает существенную часть её энтропии.