Раздел 6. Сложное сопротивление

Сложным сопротивлением называют различные комбинации простых деформаций бруса — растяжения или сжатия, сдвига, кручения и изгиба. При этом, на основании известного принципа независимости действия сил, напряжения и деформации при сложном сопротивлении определяют суммированием напряжений и деформаций, вызванных каждым внутренним усилием, взятым в отдельности.

Из большого числа возможных видов сложного сопротивления бруса мы будем рассматривать один из них — изгиб с кручением.

Изгибу с кручением подвергаются валы в зубчатых и ременных передачах, в результате чего в поперечных сечениях вала действуют нормальные и касательные напряжения.

При расчете на совместное действие изгиба и кручения, как правило, учитывают нормальные напряжения от действия изгибающего момента и касательные напряжения от действия крутящего момента. Касательными напряжениями от поперечной силы при расчетах валов обычно пренебрегают из-за малости этих напряжений по сравнению с касательными напряжениями от кручения.

Известно (разделы 4 и 5), что наибольшие напряжения от кручения и изгиба возникают на поверхности вала. Каждое из этих напряжений, взятое в отдельности, может быть меньше допускаемого напряжения, но одновременное их действие может оказаться для вала опасным. При совместном действии изгиба и кручения определяют приведенное или эквивалентное напряжение, используя одну из теорий прочности. Для валов механических передач, материалы которых являются пластичными, применяется третья (теория наибольших касательных напряжений) или четвертая (энергетическая теория). При этом расчеты по третьей теории дают больший запас прочности по сравнению с четвертой теорией. Если нет специальных указаний, то предварительный расчет диаметров валов механических передач выполняется по третьей теории прочности.

Если внешние силы, действующие на вал, не лежат в одной плоскости, то каждую из них раскладывают на составляющие: вертикальную и горизонтальную. Чтобы установить опасные сечения, строят эпюры крутящих моментов М_кр и изгибающих моментов М_изг в двух плоскостях — вертикальной М_в и горизонтальной М_г. Далее строят эпюры результирующего суммарного изгибающего момента М_Σизг:

, (6.1)

Если непосредственно по эпюрам М_кр и М_Σизг нельзя достоверно установить опасное сечение, то проверяют прочность вала в нескольких сечениях. Проверка прочности производится по расчетному (эквивалентному) моменту, величина которого по принятой нами третьей теории прочности равна:

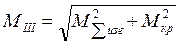, (6.2)

где М_III – расчетный эквивалентный момент по третьей теории прочности, кНм;

М_Σизг – суммарный изгибающий момент в данном сечении, кНм;

М_кр – крутящий момент в том же сечении, кНм.

Условие прочности при изгибе с кручением имеет вид:

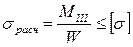, (6.3)

Формула (6.3) имеет аналогичный вид и физическую сущность, что и условие прочности при изгибе балки, только значение расчетного эквивалентного момента вычисляется с учетом дополнительного нагружающего эффекта от кручения.

В формуле (6.3)

σ_расч — расчетное эквивалентное напряжение от действия нормальных напряжений изгиба и касательных напряжений кручения, кН/см²;

W — момент сопротивления вала на изгиб, см³.

Для круглого вала (как известно)

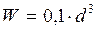, (6.4)

Практическая работа №6

Для вала, несущего три шкива, вращающегося со скоростью n (об/мин) и передающего мощность Р (кВт) построить эпюры крутящего и изгибающего моментов и подобрать из условия прочности диаметр вала d. Диаметр ведущего шкива D₁ два других ведомых шкива имеют одинаковые диаметры D₂ и каждый из них передает мощность Р/2. Ветви ремня ведущего шкива расположены в вертикальной плоскости, а двух других ведомых шкивов — в горизонтальной плоскости. Материал вала — сталь с [σ].

Конструктивные схемы валов со шкивами приведены на рис. 6.1. Данные своего варианта взять из табл. 6.1.

Схема I Схема II Схема III

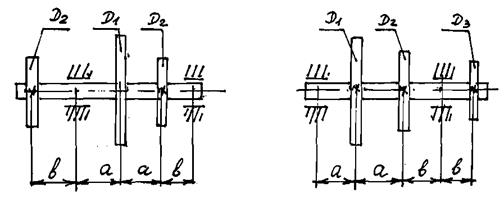
Схема IV Схема V

Сечение по ведущему шкиву Сечение по ведомому шкиву

Рисунок 6.1 – Конструктивные схемы валов со шкивами

Таблица 6.1 – Исходные данные для выполнения практической работы №6

Исходные данные	Варианты
Схема	I	II	III	IV	V	I	II	III	IV	V
n, об/мин
Р, кВт	2,0	2,4	2,6	2,7	2,8	2,9	3,0	2,5	2,6	2,7
D1, м	0,6	0,7	0,8	0,9	1,0	1,1	1,2	1,3	0,6	0,8
D2, м	0,4	0,5	0,6	0,7	0,8	0,9	1,0	1,1	0,5	0,7
а, м	0,5	0,6	0,7	0,8	0,9	1,0	1,1	1,2	0,5	0,6
b, м	0,3	0,4	0,5	0,9	1,0	0,6	0,7	0,8	0,7	0,8
[σ], кН/см2
Исходные данные	Варианты
Схема	I	II	III	IV	V	I	II	III	IV	V
n, об/мин
Р, кВт	2,8	2,9	3,0	3,2	2,4	2,6	2,8	3,0	3,2	3,4
D1, м	0,9	1,0	1,1	0,8	0,9	0,5	0,6	0,7	0,8	0,9
D2, м	0,4	0,6	0,7	0,5	0,6	0,3	0,4	0,5	0,6	0,7
а, м	0,7	0,8	0,9	1,0	1,1	0,5	0,6	0,7	0,8	0,9
b, м	0,5	0,6	0,7	1,1	1,2	0,4	0,5	0,6	0,9	1,0
[σ], кН/см2
Исходные данные	Варианты
Схема	I	II	III	IV	V	I	II	III	IV	V
n, об/мин
Р, кВт	3,6	2,8	3,0	3,2	3,4	3,6	3,8	4,0	2,8	3,0
D1, м	1,0	1,1	1,2	1,0	1,1	1,2	1,3	1,2	0,5	0,6
D2, м	0,8	0,9	1,0	0,7	0,8	0,9	1,0	0,9	0,4	0,5
а, м	1,0	1,1	1,2	0,5	0,6	0,7	0,8	0,9	1,0	1,1
b, м	0,6	0,7	0,9	0,7	0,8	0,6	0,7	0,8	1,2	1,3
[σ], кН/см2

Пример выполнения работы №6.

Дано: n=700 об/мин; Р = 7,4 кВт; D₁ = 1,0 м; D₂ = 0,7 м; а = 0,8 м; b = 0,6 м; [σ] = 54 кН/см²

Решение. 1. Изображаем расчетную схему вала в соответствии со своим вариантом. Под расчетной схемой вала оставляем место для эпюр крутящих М_кр и изгибающих М_изг моментов (рис. 6.2).

2. Определяем вращающие моменты на шкивах, используя зависимость между мощностью и скоростью вращения, которая в нашем случае имеет вид:

.

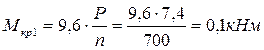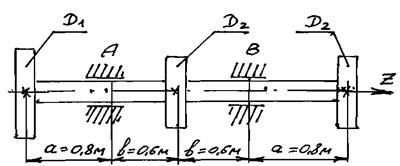
а) схема нагружения вала вращающими моментами

б) схема нагружения вала в вертикальной плоскости

в) схема нагружения вала в горизонтальной плоскости

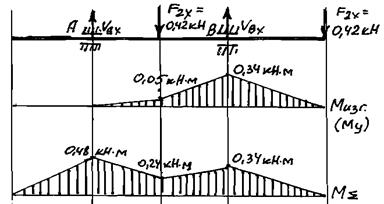
Рисунок 6.2 – Расчетные схемы вала в вертикальной и горизонтальной плоскостях и эпюры внутренних силовых факторов

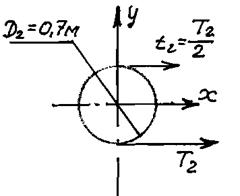Сечение вала по ведущему шкиву Сечение вала по ведомому шкиву

Рисунок 6.3 – Направление натяжения ветвей ремней в ведущем и

ведомых шкивах

Так как передаваемая валом мощность распределяется между ведомыми валами поровну, то вращающие моменты на ведомых валах одинаковы и равны:

3. Изображаем расчетную схему для определения крутящих моментов (а) и строим эпюру крутящих моментов (б).

4. Определяем окружные усилия из условий

;

;

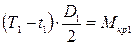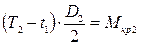Так как согласно заданным условиям Т=2t, получаем

;

.

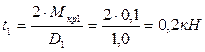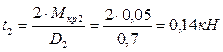5. Определяем вертикальные и горизонтальные составляющие внешней нагрузки, действующей со стороны шкивов на вал:

F_1y=T₁+t₁=3•t₁=3•0,2=0,6 кН

F_2х=T₂+t₂=3•t₂=3•0,14=0,42 кН

6. Изображаем расчетную схему для определения изгибающих моментов в вертикальной плоскости (в).

7. Определяем опорные реакции от вертикальных составляющих нагрузки

ΣМ_А=F_1y•a+V_By•2b=0

откуда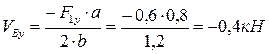

Знак "минус" показывает, что предварительно выбранное направление реакции V_Ву необходимо заменить на противоположное, т.е. реакция V_Ву направлена вниз, а не вверх.

ΣМ_В=F_1y•(a+2b)-V_А•2b=0,

откуда .

Проверяем правильность нахождения опорных реакций в вертикальной плоскости, используя третье уравнение равновесия статики

ΣF_y=-F_1y+V_Ау- V_Ву = -0,6 + 1,0 - 0,4 = 0

Реакции опор определены правильно.

8. Определяем изгибающие моменты в вертикальной плоскости и строим эпюру М_{изг В} (М_Х) (г)

В опоре А

М_изг = -F_y•a =0,6•0,8 = 0,48 кНм

В опоре В

М_изг = -F_y•(a+2b)+V_A•2b= -0,6•2,0+1,0•1,2=0

9. Изображаем расчетную схему для определения изгибающих моментов в горизонтальной плоскости. Условно переводим внешние горизонтальные нагрузки в вертикальную плоскость.

10. Определяем опорные реакции от горизонтальных составляющих нагрузки.

ΣМ_А=-F_2х•b+V_Вх•2b- F_2х•(2b+а)=0

откуда

ΣМ_В=- V_Ах •2b +F_2х•b - F_2х•а =0

Откуда

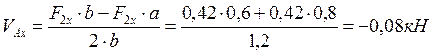
Знак «минус» указывает, что реакция V_А направлена вниз.

Проверяем правильность нахождения опорных реакций в горизонтальной плоскости по аналогии с вертикальной плоскостью:

ΣХ=-V_Ах- F_2х+V_Вх -F_2х = -0,08-0,42+0,92-0,42=0

Реакции опор определены правильно.

11. Определяем изгибающие моменты в горизонтальной плоскости и строим эпюру М_{изг Г} (М_Х) (е).

В опоре А

М_изг = 0

В сечении

М_изг = V_Aх•b= 0,08•0,6=0,05 кНм

В опоре В

М_изг = V_Aх •2b+ F_2х•b= 0,08•1,2+0,42•0,6=0,34 кНм

12. Определяем суммарные изгибающие моменты и строим их эпюру

В опоре А

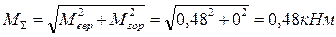
В сечении С (под шкивом 2, расположенным между опорами)

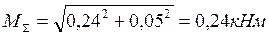
В опоре В

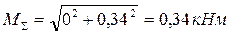
Анализ эпюр М_кр и М_Σ достоверно показывает, что наиболее опасным сечением вала является сечение в опоре А.

13. Определяем расчетный момент в опоре А по третьей теории прочности

.

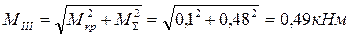14. Из условия прочности определяем диаметр вала. Все величины необходимо подставлять в одинаковой размерности.

М_III = 0,49 кНм = 49 кНсм

.

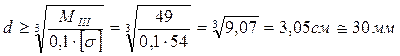Контрольные вопросы к разделу № 6

1. Что называется сложным сопротивлением?

2. В какой последовательности выполняется расчет валов, работающих на изгиб с кручением?

3. Как вычисляется расчетный эквивалентный момент?

4. Как записывается условие прочности при изгибе с кручением?