Полюс или нуль на действительной оси

Сначала рассмотрим амплитудно-частотные и фазочастотные характеристики для полюсов, расположенных на действительной оси. Затем обобщим полученные результаты на нули, используя обратную зависимость между полюсом и нулем.

Ярким примером системы с полюсом на действительной оси является фильтр низких частот. Передаточная функция H (p) = 1/(1 + pτ) имеет один полюс p = –1/τ. Амплитудная и фазовая характеристики определяются выражениями:

|H (jω)| = 1/ 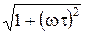; arg H (jω) = –arctg (ωτ),

где τ = RC.

Прежде чем анализировать аналитическое выражение, используем графическое построение для общего представления происходящего. Диаграмма для одного полюса показана на рис. 26. На нем показаны три стрелки, соответствующие трем разным частотам. Для самых низких частот (вблизи ω₁) модуль М фактически постоянен и угол ψ близок к нулю. При увеличении частот модуль начинает неограниченно расти, а угол увеличиваться, стремясь в пределе к 90°. Границу между областями нижних и верхних частот можно примерно провести при ω = 1/τ (аналогично ω₂ на рис. 26). Для частот ниже 1/τ модуль М слабо зависит от частоты, а для частот, много больших 1/τ, модуль М изменяется примерно пропорционально частоте.

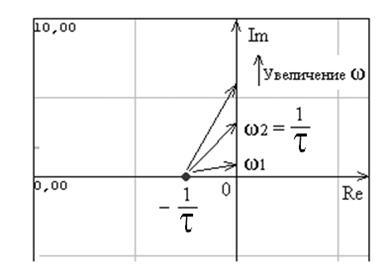
Рис. 26. Диаграмма для полюса на вещественной оси

Следует иметь в виду, что изменения М отражаются на знаменателе |H (jω)|, а изменения фазы равны ψ. Поэтому можно сделать вывод, что для одиночного полюса в точке 1/τ амплитуда примерно постоянна для ω << 1/τ и пропорциональна 1/ω для ω > 1/τ, а фаза близка к нулю для ω << 1/τ и составляет около 90° для ω > 1/τ.

Из анализа выражений |H (jω)| и arg H (jω) можно получить те же результаты. Рассматривая сначала выражение для модуля, видим, что, если ω << 1/τ, его величина равна 1. Если же ωτ >> l, этот член преобладает в знаменателе и амплитуда примерно равна 1/ωτ. Эти два крайних случая для изменения частоты и соответствующие приближенные значения амплитуды определяют ее асимптотическое поведение:

низкочастотная асимптота: ωτ << 1, |H (jω)| = 1;

высокочастотная асимптота: ωτ >> 1, |H (jω)| = 1/ωτ.

Первая из этих асимптот, соответствующая низким частотам, представляет собой постоянную величину, как это и должно быть в резистивной цепи. Вторая асимптота, соответствующая высоким частотам, ведет себя аналогично тому, как если бы полюс находился в начале координат. Поэтому можно ожидать, что для достаточно высоких частот график |H (jω)| в зависимости от ω в двойном логарифмическом масштабе будет иметь наклон –1. Эти асимптоты исключительно удобны для определения примерной формы амплитудно-частотной характеристики.

Отметим, что асимптоты сопрягаются на частоте, где значение второй асимптоты 1/ωτ равно значению первой асимптоты, т. е. 1/ωτ = 1. Частота сопряжения асимптот ω_p = l/τ. Она также соответствует по величине положению полюса и называется частотой полюса передаточной функции. Частота полюса f_p = 1/2 πτ.

На рис. 27 вычерчены обе асимптоты в двойном логарифмическом масштабе, сопрягающиеся на частоте полюса. Также показана точная зависимость |H (jω)| от f. Наибольшие отклонения асимптот от точной зависимости наблюдаются на частоте полюса. Оценим величину отклонения асимптоты от точного решения.

Если f = 1/2πτ, модуль |H (j2πf)| = 1/ 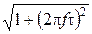= = 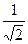0,707, или в децибелах: 20 lg 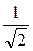= –3 дБ.

Следовательно, на частоте полюса модуль меньше на 3 дБ. Обычно частотные границы систем определяются по уменьшению уровня частотной характеристики на 3 дБ ниже некоторого определенного заранее. Можно довольно быстро построить график амплитудно-частотной характеристики с одним полюсом, если учесть, что низкочастотная асимптота представляет ее постоянной до частоты полюса, а потом высокочастотная асимптота – убывающей с наклоном –1. На частоте полюса наносится точка на 3 дБ (или в 0,707 раза) ниже низкочастотной асимптоты. На частотах в 2 раза выше и в 2 раза ниже частоты f_p погрешность асимптотической аппроксимации составляет –1 дБ. Соединяя показанные на рис. 27 точки плавной кривой, можно очень быстро построить АЧХ. Такие построения весьма полезны при оценке характеристик цепей. Они известны как графики или диаграммы Боде [6].

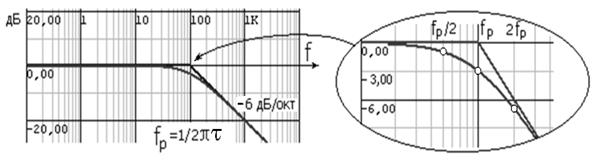
Рис. 27. Амплитудно-частотная характеристика

для одиночного полюса в точке p = –1/τ

Аналогично можно оценить изменения фазы с частотой. Для очень низких частот модуль частотной характеристики постоянен. Так как постоянство амплитуды соответствует поведению резистивной цепи, можно ожидать, что фаза на низких частотах примерно равна нулю.

Поскольку изменение амплитуд на высоких частотах аналогично изменению амплитуд для полюса в начале координат, можно ожидать, что на достаточно высоких частотах угол будет близок к –90°. Точная кривая для зависимости фазы от частоты показана на рис. 28, где приведены также асимптоты, используемые при проведении быстрых оценок.

Для частот ниже 1/10 частоты полюса фазовый угол близок к нулю, а для частот, в 10 раз превышающих частоту полюса, примерно равен –90°. На частоте полюса (ωτ = 1) фаза определяется как –arctg 1, который равен –45°. Ломаная линия кусочно-линейной аппроксимации фазочастотной характеристики (рис. 28) использует все эти особенности. Она равна нулю до 1/10 частоты полюса, плавно убывает, проходя через –45° на частоте полюса, до –90° при частотах f ≥ 10f_p и далее остается постоянной.

Это приближение к точной кривой имеет погрешность не более 7° во всей области частот и очень удобно для быстрой оценки поведения цепей. На рис. 29, а, б приведены частотные характеристики для нуля, находящегося на отрицательной части действительной оси.

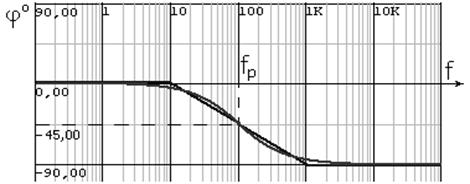
Рис. 28. Фазочастотная характеристика для одиночного полюса в точке p = –1/τ

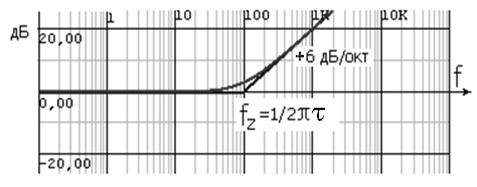
Рис. 29, а. Амплитудно-частотная характеристика для нуля,

находящегося на отрицательной части действительной оси

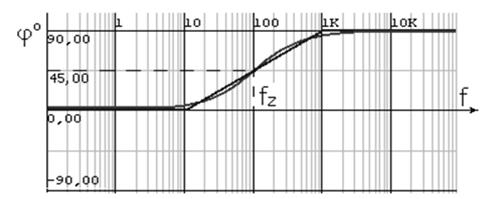
Рис. 29, б. Фазочастотная характеристика для нуля,

находящегося на отрицательной части действительной оси

Предполагается, что нуль расположен в точке p_a = –2πf_z. Отметим, что амплитудная и фазовая характеристики для нуля идентичны характеристикам для полюса, за исключением того, что каждая кривая является перевернутой. Амплитуда постоянна до частоты, соответствующей положению нуля, а затем растет с наклоном +1, тогда как фаза равна нулю на низких частотах, проходит через +45° на частоте нуля и на высоких частотах становится постоянной, равной +90°.

Комплексно-сопряженные пары

Совершенно иная ситуация может иметь место в цепи, описываемой уравнением второго порядка. Для примера возьмем структуру с передаточной характеристикой

.

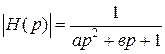Корни этого уравнения определяются выражением

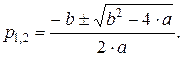
Учитывая, что добротность 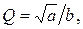упрощаем выражение и получаем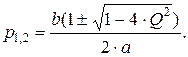

В зависимости от того, какое значение принимает добротность, получаются либо действительные корни (Q ≤ 0,5), либо комплексно-сопряженные корни (Q > 0,5). При Q = 0,5 корни кратные (рис. 33).

При Q < 0,5 два полюса расположены на действительной оси (рис. 30, а), с увеличением добротности Q они стремятся друг к другу (рис. 30, б). При Q = 0,5 полюса кратные (рис. 30, в), а при Q > 0,5 полюса комплексно-сопряженные (рис. 30, г).

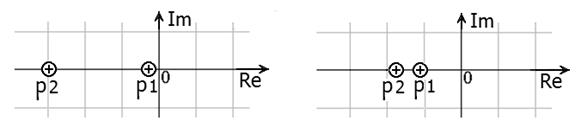
а) б)

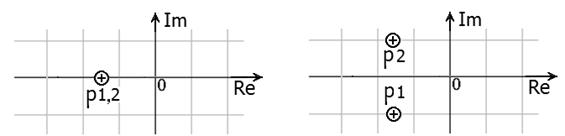
в) г)

Рис. 30. Диаграммы полюсов

На рис. 31–34 представлены амплитудно-частотные характеристики с передаточной функцией при различных значениях Q.

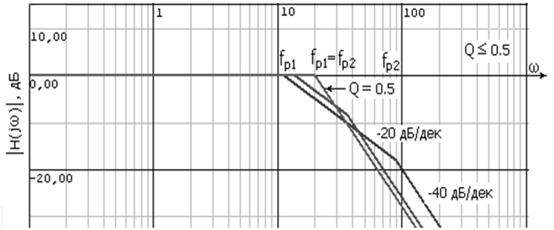
Рис. 31. Амплитудно-частотные характеристики при Q ≤ 0,5

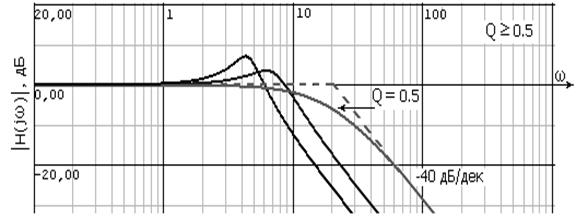
Рис. 32. Амплитудно-частотные характеристики Q ≥ 0,5

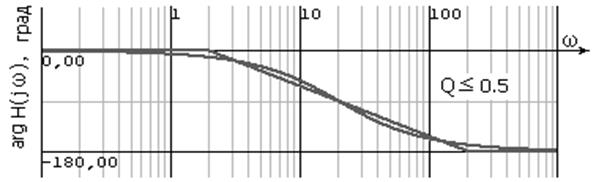
Рис. 33. Фазочастотная характеристика при Q ≤ 0,5

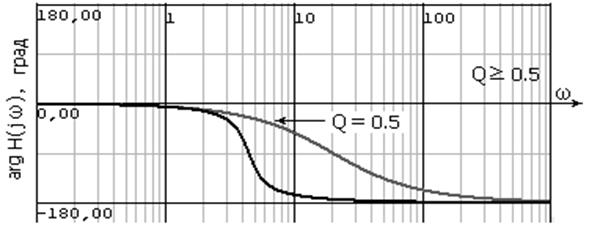
Рис. 34. Фазочастотная характеристика при Q ≥ 0,5

Глава 4