Оптимизация конструктивных параметров пневматического уравновешивающего механизма

Рассмотрим задачу оптимального параметрического синтеза конструкции пневматического уравновешивающего механизма (УМ). Подобные механизмы, как известно, не обеспечивают полного уравновешивания качающейся части в пределах заданного диапазона углов возвышения ствола. Тем

не менее соответствующий подбор конструктивных параметров механизма позволяет получить моменты неуравновешенности, допускаемые эксплуатационными ограничениями нагрузки на механизм, вертикальной наводки.

До недавнего времени решение этой задачи представляло значительные трудности, вызываемые большим числом переменных, наличием различного рода конструктивно-компоновочных ограничений, определяющих область изменения переменных. Привлечение алгоритмов оптимального управления процессом поиска рациональных сочетаний конструктивных: параметров УМ позволяет за короткое время подобрать на ЭВМ оптимальную конструкцию.

Впервые эта задача была решена Н. Н. Худковым и В. В. Самковичем. При этом уравновешивающий механизм в качестве объекта для оптимального синтеза был выбран не случайно. Это один из немногих узлов артиллерийского орудия, функционирование которого описывается сравнительно простой и малоразмерной математической моделью, а качество конструкции характеризуется ярко выраженной скалярной функцией цели — моментом неуравновешенности качающейся части.

В терминах математического программирования задача формулируется следующим образом: найти такие значения вектора конструктивно-настраиваемых параметров 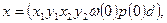которые минимизируют па заданном отрезке углов возвышения ствола 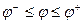наибольшее значение модуля момента неуравновешенности

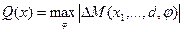
в области R, задаваемой конструктивно-компоновочными, технологическими и эксплуатационными ограничениями

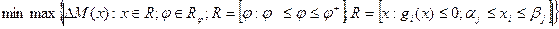
Здесь х₁, у₁ — координаты подвижной опоры на люльке при 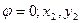— координаты неподвижной опоры на верхнем станке; v(0), р(0) — объем и давление воздуха при 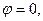, d — диаметр поршня.

Область R определяется следующими ограничениями.

1. Минимальное расстояние между подвижной опорой на люльке и неподвижной опорой на верхнем станке должно быть достаточным, чтобы разместить между опорами конструкцию УМ:

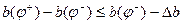
если механизм толкающего типа;

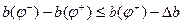
если механизм тянущего типа.

Здесь 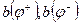— наибольшее и наименьшее расстояния между опорами; 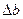— размер под конструктивное оформление опор, поршня, уплотнений и др.

Записывая неравенства в форме односторонних ограничений, получим

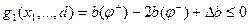
при тянущем уравновешивающем механизме

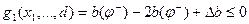
при толкающем уравновешивающем механизме

2. Минимальное давление в рабочей полости УМ (при наибольшем угле возвышения ствола) не должно превышать заданного уровня, обусловленного возможностями стандартных устройств для заправки УМ воздухом. Например, в буксируемых орудиях заправка УМ воздухом производится специальными пневмогидравлическими насосами, рассчитанными на вполне определенные давления. Таким образом,

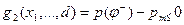
где р_m— наибольшее давление, обеспечиваемое заправочным устройством.

3. Из конструктивно-компоновочных соображений на вектор оптимизируемых параметров х = (x₁ .. . , d) накладываются двусторонние ограничения;

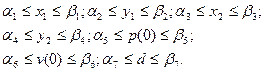
Связь между конструктивно-настраиваемыми переменными х и параметрами состояния УМ устанавливается математической моделью функционирования УМ. Если пренебречь статическими сопротивлениями в подвижных сочленениях УМ, а состояние газа в рабочей полости подчинить уравнению политропы, то математическая модель представляется в виде (рис. 4.11)

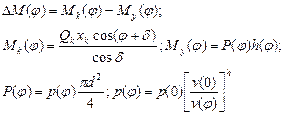
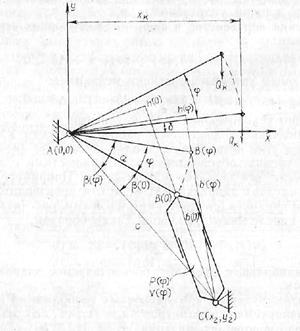
Рис. 4.11. Кинематическая схема УМ

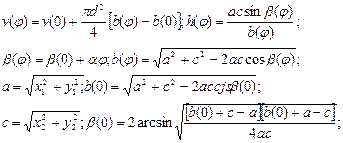
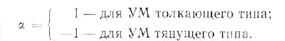
На рис. 4.11 и в модели функционирования УМ приняты следующие обозначения: А (0, 0)—-след от пересечения оси цапф с плоскостью чертежа (начало координат); В(x₁, y₁) — подвижная опора на люльке при 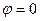; 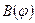— подвижная опора при текущем значении угла 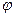; Q_k — вес качающейся части; х_k— смещение центра тяжести относительно оси цапф; 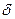— угол, характеризующий положение центра тяжести качающейся части при 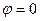; 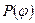— текущее усилие на штоке УМ; 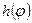— плечо силы Р( 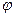) относительно оси цапф; с(х₂, у₂)—неподвижная опора на верхнем станке; а, с,

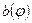— стороны разре­шающего треугольника AВС; 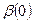, 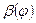— угол при вершине А при φ = О и при текущем значении угла φ; ΔM(φ), M_K(φ), Му(φ) -- соответственно момент неуравновешенности, момент от веса качающейся части и момент, создаваемый УМ; п — показатель политропы.

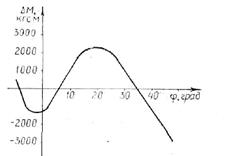
Рис. 4.12. Характер изменения момента неуравновешенности ΔМ(φ)

Данная минимаксная задача оптимизации относится к классу задач нелинейного программирования, где функция цели не является дифференцируемой в области задания переменных. Покажем, как можно свести ее к дискретной минимаксной задаче с гладкими дифференцируемыми функциями.

Анализ модели функционирования УМ и ограничений показывает, что ΔМ(х, φ), g₁(x) и g₂(x) непрерывны, т.е. эти функции гладкие в заданной области R. Тем не менее ΔM{x, φ) в некоторых точках недифференцируема, поскольку на заданном промежутке углов возвышения она может дости­гать экстремальных значений более чем в одной точке (рис. 4.12). Поэтому задачу приходится формулировать приближенно, заменяя функцию ΔМ(х, φ) при каждом значении вектора xk ее точками, достаточно строго ее моделирующим (рис.4.13):найти

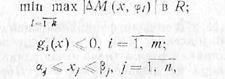
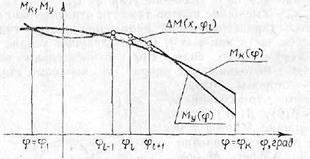
Рис. 4.13. Дискретное моделирование функции ΔМ(х, φ)

где т = 2, п = 7.

Далее, путем введения в задачу дополнительной переменной х_п+1 и k дополнительных ограничений, получаем новую задачу, эквивалентную предыдущей: найти

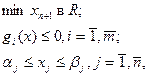
где т = k + 2, n=8; g₁(x), g₂(x) определены выше, а для i>2 —g_i(x) = \ΔМ(х, φ _i_₂)|—х_n+1 i=3, k + 2.

Чем больше k, тем меньше x_n+1, т. е. тем в меньшей степени решение данной задачи отличается от задачи, где надо найти

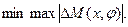
Дискретная минимаксная задача с ограничениями в виде неравенств путем введения дополнительной переменной свелась, таким образом, к задаче нелинейного программирования с гладкими дифференцируемыми функциями.

Приведем пример оптимизации конструктивных параметров УМ методом возможных направлений. Требовалось найти значения х₁ ,у_ь ,х₂ ,y₂, p(0), и(0), х_п+1 которые минимизируют х_п+1 в области R, задаваемой ограничениями

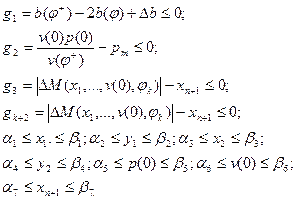
Задача решалась с исходными данными, соответствующими УМ 122-мм гаубицы Д—30: Q_k = 1483 кг, х_k = 119,6 см, Δb = 20 см, р_т = 63,5 кг/см³, φ ^- = — 7°, φ + - 50°, α₁ = 20 см, β₁ = 30 см, α₂ = 10 см, β₂ = 20 см, α₃ - 80 см, β₃= 95 см, α₄ = —60 см, β₄ = —40 см, α₅ = 80 кг/см², β₅ = 120 кг/см², α₆ = 4000 см³, β₆ = 6000 см³.

Диаметр поршня не варьировался и был принят d = 9,5 см, В гаубице Д-30 УМ комбинированный, пневмопружинный. Дополнительный упругий элемент — пружина, корректирующая силовую характеристику УМ, включается при φ = 50°. В связи с этим, в данном примере верхняя граница диапазона углов возвышения ствола принята равной φ = 50°. Значения φ₂, ..., φ _k-1 находились из формулы

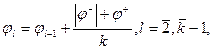
где k — принимаемое число дискретных значений углов возвышения ствола.

Результаты решения оптимизационной задачи приведены па рис. 4.14. По осям ординат откладывались значения оптимизируемых параметров, по осям абсцисс — число итераций. Сходимость параметров к оптимальному значению проверялась решением задачи при различных исходных векторах конструктивно-настраиваемых параметров х. С целью проверки сходимости варьировалось также, число дискретных точек к

Из графиков рис. 4.14 следует, что оптимальный вектор параметров УМ имеет следующий вид: координаты верхней опоры х₁ = 24 cм, y₁, — 10 см; координаты нижней опоры

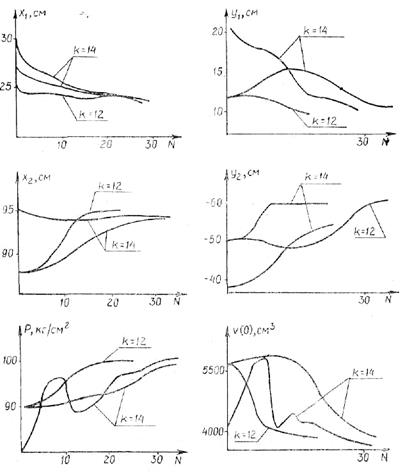
Рис. 4.14. Сходимость конструктивно-настраиваемых параметров к оптимальному значению

x₂= 95 см, у₂ = - 60 см; давление воздуха р(0) = 100 кг/см²; объем воздуха u(0) = 4000 см³. При этом момент неуравновешенности качающейся части принимает минимальное значение max \ΔМ\ = 3000 кгс • м.

На решение задачи методом возможных направлений, как видно из рис. 4.15,-требуется около 30 итераций. Время счета одной итерации на ЭВМ составляет 0,5—2 мин.

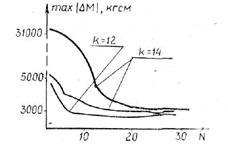
Рис. 4.15. Поведение целевой функции в процессе итеративной процедуры оптимального поиска

Задача оптимизации параметров пневмогидравлического досылателя полевого орудия по критерию стабильности функционирования

Схема пневмогидравлического досылателя приведена на рис. 4.16. При накате цилиндр ускорителя встает на упор.

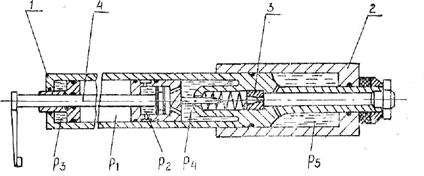
Рис. -1.16. Схема пневмогидравлического досылателя: / - цилиндр ускорителя; 2 - рабочий цилиндр; 3- клапан; 4 - шток

Приняты следующие обозначения; M₁ — масса выстрела; x₁ — перемещение выстрела; М₂ — масса штока; x₂ — переме­щение штока; М₃ — масса цилиндра ускорителя; x₃ — перемещение цилиндра ускорителя; р₁ ,р₂ , p₃, p₄, p₅ — Давление жидкости в полостях досылатсля; А₁,A₂, А₃, A₄, А₅ —соответст­вующие рабочие площади досылателя; р₁, w_1о — начальные давления и объем газа в рабочем цилиндре (в невзведенном состоянии); F_K — сила взаимодействия между выстрелом и клодцем; /_к — длина хода клоца; T_i — силы трения;'А_x — пло­щадь отверстия истечения клапана; 0 — показатель политро­пы; у - удельный вес жидкости; с_к — жесткость клоца. Модель процесса функционирования досылатсля:

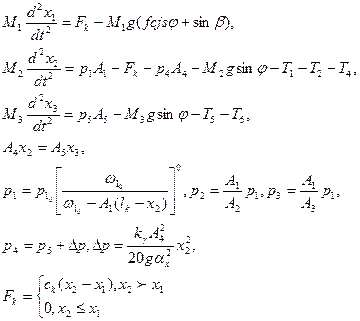
Начальные условия;

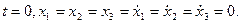
Расчет при заданных значениях конструктивных величин рассматриваемого досылзтеля 122-мм орудии (в том числе а_х = 0,66В см², p₁ = 25 кгс/см²) показал значительное отличие (нестабильность) конечных скоростей досылки при Ψ = 0 и Ψ= Ψ_max углах возвышения для одного типа выстрела {рис. 4.17).

Рассматривается задача обеспечения стабильности скорости в конце досылки dx₁/dt при заданных ограничениях в виде неравенств на Ψ— углы наведения, k — коэффициенты сопротивления истечению жидкости, изменяющиеся вследст­вие нагрева жидкости, и М, — массу выстрела, изменяющую­ся в зависимости от типа снаряда. Оптимальным будет досылатель, который в указанной области (G_ψ, G_k, Gm₁) изменения ψ, k, Mi обеспечивает

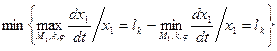
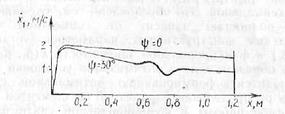
Рис. 4.17. Результаты расчета скорости досылки

Параметры, которые можно варьировать при конструиро­вании досылателя, —a_x ,p₁,ώ₁,M₂, М₃, с_к - На эти параметры задаются ограничения из условий конструктивной целесообразности. Оказалось что min целевой функции достигается на верхних границах значений, ώ₁, M₂, М₃, с_{к .}Поэтому варьировались только а_x- и p₁ .

Результат поиска представлен на рис. 4

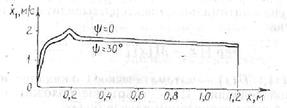
Рис. 4,18. Результаты расчета скорости досылки ■ после оптимизации

Решение: а_х - 0,80 см², p₁= 36,2 кгс/см²

Задана уточнения конструктивных параметров

элементов артиллерийского орудия с учетом требования по надежности функционирования

Исходя из общих физических соображений, конструкцию можно считать оптимальной по надежности тогда, когда конструктивные параметры ее элементов с учетом режимов функционирования выбраны такими, что при плотности распределения f_опт (β₁,β₂, . ..,β_r) вероятность вер (х ?[х]) будет максимальной. Это обусловлено тем, что закон распределения полностью зависит от совместной плотности распределения конструктивных параметров установки f(β₁,β₂, . ..,β_r) и функциональной зависимости x(β₁,β₂, . ..,β_r) .

Таким образом, задача оптимизации установки по надежности сводится к формированию оптимальной совместной плотности распределения параметров ее элементов f_опт с учетом режимов работы и функциональной связи параметров элементов с выходными параметрами арторудия х.

Пусть дан вектор {β} с составляющими (β₁,β₂, . ..,β_r), у которых совместная плотность распределения f(β) =f(β₁,β₂, . ..,β_r). Известна также функция x= x(β₁,β₂, . ..,β_r), которая должна находиться в допустимой об­ласти x?[х]. Необходимо определить такие значения β₀чтобы вер (х ? [х]) была максимальной.

Поскольку расчет вероятностных характеристик даже при использовании современных ЭВМ связан с трудоемкими вычислениями, целесообразно формулировку задачи изменить таким образом, чтобы иметь возможность оперировать исключительно детерминированными величинами. Критерий для определения оптимального вектора выводится из неравенства Чебышева:

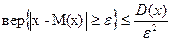
где М(х), D(x) -математическое ожидание и дисперсия случайной величины х; ε — некоторое положительное число, которое в рассматриваемом случае будет

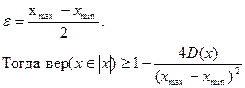
Это неравенство не зависит от закона распределения случайной величины X. Анализируя последнее выражение, можно сделать вывод, что если потребность максимума вер(х ?[x]),то это равносильно обеспечению такого вида закона распре­деления x, которому соответствует минимум дисперсии D(x):

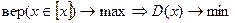
Любая непрерывная функция случайных аргументов х = x(β₁,β₂, . ..,β_r) cточностью до множителя второго по­рядка может быть представлена в виде

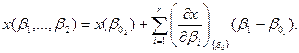
в окрестности β₀= M(βi) математического ожидания слу­чайных аргументов. Тогда дисперсия

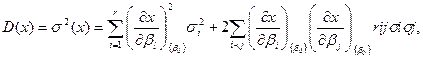
где σ — среднее квадратическое отклонение по параметру β_i;; rij — коэффициент корреляции между i-м и j-м аргументами.

Таким образом, σ(х) является функцией β_о. и σ_i

Так как необходимо минимизировать дисперсию, то эта операция должна осуществляться по параметрам β_о, и σ_i;.

Очевидно, что σ²(х) будет минимальным в том случае, когда σ_i = 0. Однако этот тривиальный случай мало интересен, так как конструктивные параметры элементов арторудия всегда обладают какой-то конечной, не равной нулю дисперсией. Поэтому необходимо проводить минимизацию σ²(х) по пара­метрам β_о для какого-то вполне определенного вектора σ_k = σ_k(σ_k,…, σ_k), Практически σ_k может быть получено бесконечным числом сочетаний, поэтому целесообразно искать минимальное значение дисперсии σ²(х) относительно σ_i; в среднем, учитывая всю возможную область изменения σ_i;.

Чтобы не учитывать физическую природу и размерность каждого конструктивного параметра, производится нормировка σ²(х) по М(х) и M(β)=β₀ .

Тогда

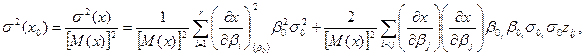
где σ_0; — относительное значение среднего квадратического отклонения по параметру β_i т. е. .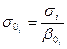

Для усреднения σ²(х_о) по σ₀ можно воспользоваться следующим результатом:

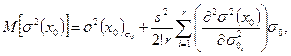
где индекс σ₀ при σ² (x₀))_σ и 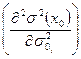указывает на то, что значения этих величин вычислены при σ_0i = σ₀ ,а s - некоторое положительное число второго порядка малости.

Тогда

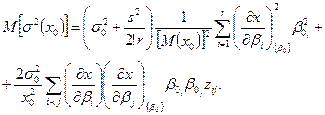
Так как необходимо минимизировать это выражение по параметрам β₀, , то постоянные множители можно опустить.

В этом случае минимизируемая функция может быть представлена в виде

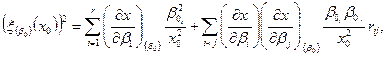
где 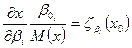представляют собой нормированные коэффициенты влияния.

Тогда минимизируемая функция представляет собой суммарную чувствительность по всем конструктивным элементам:

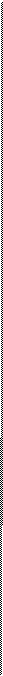
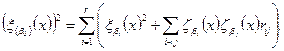
Если r_ij= 0, то выражение упрощается:

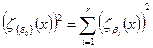
Таким образом, чтобы достигнуть оптимума надежности конструкции арторудия или его агрегатов, необходимо определить такие значения параметров β_i, чтобы суммарная чувствительность для всех элементов была минимальна с учетом ограничений функционального и физического характера, накладываемых на минимизируемые функции.

Пример. Рассматривается решение задачи уточнения конструктивных параметров компенсатора жидкости тормоза откатных частей для автоматической артиллерийской установки.

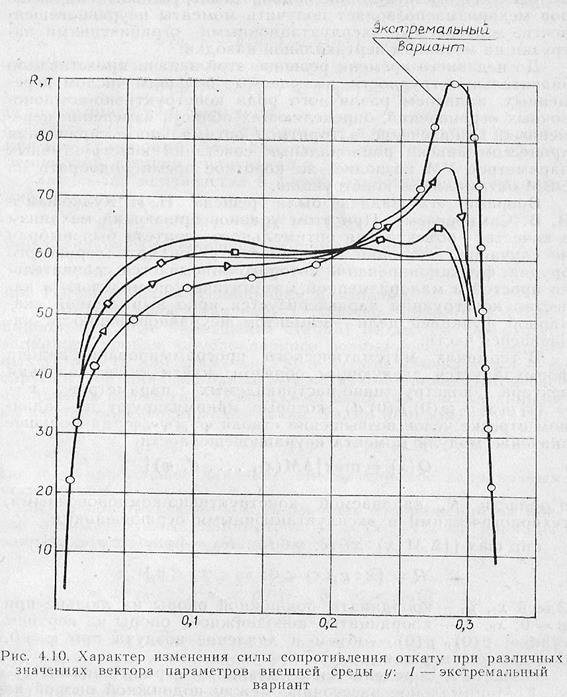
Целевой функцией здесь является суммарная чувствитель­ность разброса значений скорости откатных частей в конце наката к нарнациям конструктивных параметров компенсатора. Рассмотрение движения откатных частей в конце наката объясняется необходимостью обеспечения строгих ограничений скорости конца наката v_KH сверху и снизу. Ограничение v_KH сверху обусловливается прочностью опорных узлов орудия, а также возможным падением характеристик точности стрельбы из-за колебаний элементов орудия при ударе откатных частей в крайнем переднем положении при накате; ограничение v_KH снизу связано с необходимостью исключить так называемые «ползучие скорости» на конечном участке наката.

В рассматриваемом случае движение откатных частей автоматической артиллерийской установки описывается уравнением

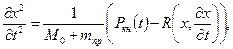
где x, 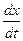, 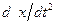— перемещение, скорость и ускорение от­катных частей; Р_kн(t)—сила действия пороховых газов; М₀ — масса откатных частей; т_пр — масса механизмов автоматики, приведенная к движению откатных частей.

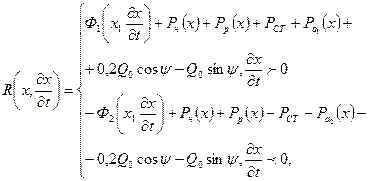
где Р_н, Р_р — соответственно, сопротивление пружины накат­ника и рекуператора; p_ст — сила трения; Q_o—вес откатных частей; ψ — угол наведения; Р_а(х), Р_а2{х)-— силасопротивления, действующая со стороны механизмов автоматики на откатные части, соответственно, при откате и накате.

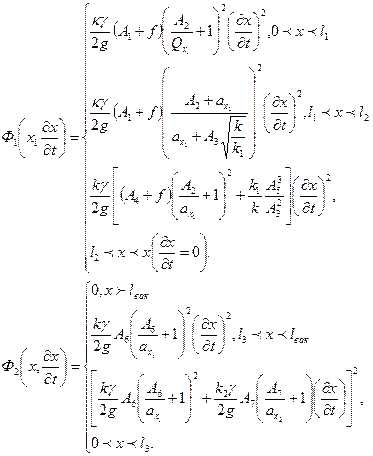
Для уяснения структуры силы гидросопротивления на рис. 4.19 приведена схема тормоза отката. Здесь

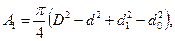
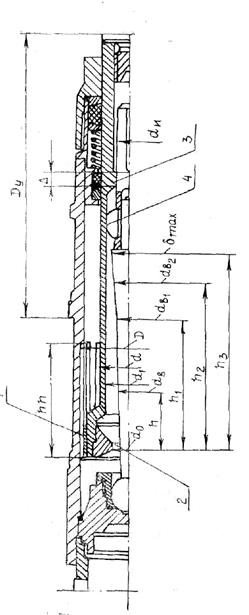
Рис. 4.19. Схема тормоза откатных частей: 1-зазор между рубашкой поршня и цилиндром; 2 — зазор между веретеном и регулирующим коль­цом; 3 — зазор между иглой и очком штока; 4—зазор между направляю­щей веретена и штоком

где D — диаметр поршня тормоза; d — диаметр штока тормоза; d₁ — внутренний диаметр штока; d_Q — диаметр регулирующего очка.

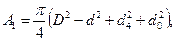
где d_н — диаметр иглы; а_х, a_x.₂ — переменная площадь отверстий истечения жидкости, соответственно, при откате и накате;

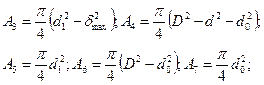
где f — характеристика сопротивления пары воротник-шток; у — удельный вес жидкости; k, k_1. ,k₂ k₃,k₄ — коэффициенты гидропотерь при протекании жидкости, соответственно, через регулирующее очко, в заверенную область, по канавкам тормоза наката, между поршнем и цилиндром, в зазор между очком штока и иглой; l₁, — перемещение откатных частей при откате до выхода иглы из цилиндра-тормоза наката; l₂ — перемещение откатных частей при откате до момента заполнения жидкостью заверетенной полости; l_вак; — перемещение откатных частей при накате до выбора вакуума; l₃ — перемещение откатных частей при накате до входа иглы в очко штока.

Поскольку наличие компенсатора жидкости вносит опре­деленные изменения в характеристики процесса движения откатных частей в конце наката, имеет смысл уточнить значения его конструктивных параметров. Для учета влияния работы компенсатора необходимо внести уточнения в матема­тическую модель процесса движения откатных частей. Уточ­нение вводится на основе рассмотрения баланса рабочей жидкости между полостью компенсатора и гидротормоза. Перемещение откатных частей при накате до выбора вакуума в нерабочей полости тормоза отката соответствует некото­рому х, при котором справедливо равенство

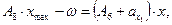
где x_max — длина отката.

За промежуток времени от начала отката до момента выбора вакуума в нерабочей полости тормоза при накате некоторый объем жидкости перетекает из компенсатора в нерабочую полость тормоза отката. После выбора вакуума в нерабочей полости тормоза отката скачком повышается давление и жидкость перетекает в компенсатор до тех пор, пока давление в нерабочей полости тормоза отката не станет равным давлению в компенсаторе. Суммарное изменение объема жидкости в гидротормозе от начала отката до текущего момента времени

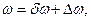
где 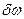— увеличение объема рабочей жидкости в тормозе с момента начала отката за счет разогрева жидкости при торможении откатных частей; Δώ— изменение объема рабочей жидкости, обусловленное ее- перетеканием из компенсатора в нерабочую полость тормоза и обратно, определяемое выражением

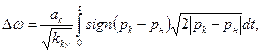
где а_k,_; — площадь отверстия, соединяющего полость компенсатора с полостью гидротормоза; р_к — давление в полости компенсатора; k_к — коэффициент гпдросопротивления при перетекании рабочей жидкости между полостями гидротормоза и компенсатора;

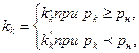
здесь р_н— давление рабочей жидкости в нерабочей полости тормоза отката, определяемое из равенства

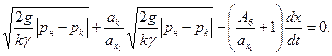
Тогда, перемещение откатных частей х =l₄при накате, соответствующее моменту выбора вакуума в рабочей полости тормоза отката, определится из равенства A₈ ∙ х— w = 0.

Вид зависимости для силы гидротормоза при накате с учетом компенсатора

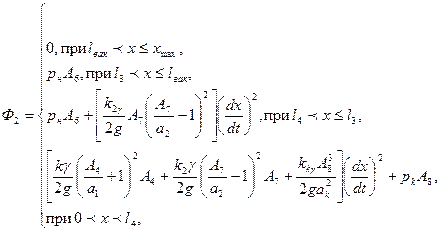
Оптимизация осуществляется с учетом изменений в пределах, предусмотренных конструкцией орудия, углов возвышения, характеристик рабочей жидкости тормоза отката, а также импульса приведенной силы давления пороховых газов на дно канала ствола.

В качестве управляющих параметров принимаются следующие параметры компенсатора: а_к; w_ж - начальный объем жидкости в компенсаторе; w_в — начальный объем газа в ком­пенсаторе.

Ограничения:

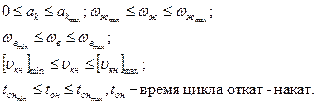
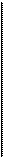В качестве" алгоритма поиска может быть использован адаптивный случайный поиск, рассмотренный ранее.

Рис. 4.20. Сходимость d_ак к оптимальному значению

В результате расчетов определяются параметры компенсатора, обеспечивающие пониженную чувствительность скорости откатных частей в конце наката к изменению таких факторов, как приведенная сила давления пороховых газов на ствол, угол возвышения, температура рабочей жидкости в тормозе откатных частей.

Характер изменения в процессе поиска величины отверстия, соединяющего полость компенсатора с полостью гидротормоза, приведен на рис. 4.20.

При этом такие параметры управления, как начальный объем жидкости и газа в компенсаторе, приняли свои граничные (штатные) значения. Найденное значение d_ак = 2,9 мм обеспечило уменьшение значения дисперсии скорости откатных частей в конце наката на 20% по сравнению со штатным.

С п и с о к литературы

1 Анализ систем оружия в США по методу «затраты-эффективность». — М.: ИМЭ и МО АН СССР, 1971, ДСП.

2. Проектирование ракетных и ствольных комплексов / Пол ред. Б. В. Орлова. — М.: Машиностроение, 1974.

3. Тараканов К. В., Овчаров Л. Л Тырышкан А. И. Аналитическиеметоды исследования систем. — М.: Сов. радио, 1974.

4. Чуев Ю В Проектирование ствольных комплексов (теоретические
основы). — №.: Машиностроение, 1976. 5

5. Чуев Ю. В., Спехова Г. П. Технические задачи исследования операций. — М.: Сов. радио,1971.