Краткие сведения из теории стрельбы

Теория стрельбы — это дисциплина, которая на основе исследования явлений, сопровождающих стрельбу, и оценки ее эффективности вырабатывает рациональные методы подготовки и ведения огня, а также предлагает исходные данные разработки требований к ствольным комплексам. Классическая теория стрельбы рассматривает процесс стрельбы огневого противодействия противника, полагая, кроме того, что орудие является абсолютно надежным. В этом ее отличие от исследования операций, где анализируются результаты стрельбы с учетом огневого противодействия противника, надежности комплекса, а изучение процессов функционирования арткомплекса не ограничивается изучением процесса стрельбы, но предполагает рассмотрение и других процессов (перемещения, управления, разведки и т.н.).

В зависимости от вида цели применяют тот или иной показатель эффективности Э, характеризующий результат стрельбы. Так, если цель одиночная (малоразмерная), то в качестве показателя применяется вероятность поражения цели Э = Р (A), где А — поражение цели. Если цель групповая (группа одиночных), используют показатель Э=МО 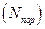—математическое ожидание числа пораженных единиц 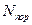. Если цель площадная (рассредоточена по площади), то в качестве показателя применяется Э = МО (S„/S_ц), где S_п — пораженная площадь, S_ц— площадь цели.

Показатели эффективности стрельбы определяются законами рассеивания снарядов и законами поражения. Явление рассеивания состоит в том, что траектория каждого снаряда в одних и тех же условиях стрельбы отличается одна от другой. Причины рассеивания изложены в подразд. 3.1 при рассмотрении боевого свойства арторудия — точности стрельбы. Дополнительно нужно иметь в виду, что рассеивание зависит также от типа снарядов (ударных, дистанционных), от способа стрельбы (одиночная, залповая, очередями), от выстрелов независимых и зависимых (зависимость характеризуется корреляцией координат точек попадания снарядов). При одиночной стрельбе выстрелы независимы. Рассеивание при одиночной стрельбе описывается законом распределения

,

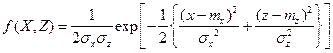где x, z—координаты точек попадания снарядов; 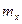, 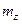— математические ожидания; 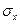, 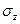— средние квадратические отклонения случайных величин х и z.

, ,

,

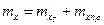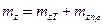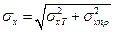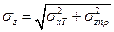
где 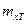, , 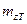, 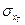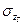—математические ожидания и средние квадратические отклонения технического рассеивания;

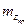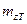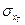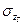, , , --математические ожидания и средние квадратические отклонения прицельного рассеивания.

Схема определения вероятности попадания в цель Р при-ведена на рис. 3.9: площадь цели разбита на элементарные прямоугольники: 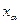, , 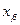, 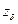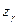— координаты вершин этих пря-моугольников.

ц [г—тг 2

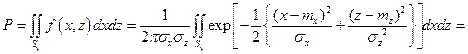
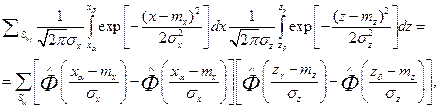
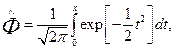
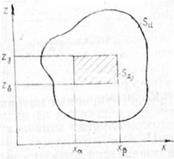где 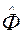—табулированная функция Лапласа. | Рассеивание при стрельбе залпами характеризуется двумя видами ошибок: ошибками первой группы - случайными (неповторяющимися) для любого снаряда в залпе и ошибками второй группы – постоянными Рис. 3.9 Представле-

(повторяющимися) для каждого ние площадной цели

снаряда в залпе, но случайными от одного залпа к другому.

Если в залпе доля повторяющихся ошибок велик, то выстрелы в залпе будут сильно зависимы.

Координаты точек попадания для i-го выстрела ,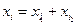

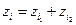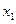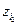, где , - составляющие координат, определяемые ошибками

первой группы, 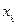, 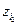-- ошибками второй группы.

Математические ожидания координат в рассматриваемом случае будут 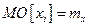, , 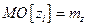а их средние квадратические отклонения

.

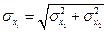
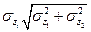Зависимость между выстрелами i и j при стрельбе залпами принято характеризовать коэффициентом корреляции раздельно по координатам х и z, т. е.

; ,

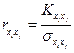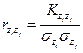Где 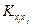, 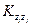—корреляционные характеристики, учиты­вающие взаимное влияние между выстрелами.

,

, .

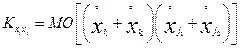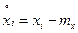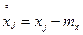Корреляционная матрица для n выстрелов

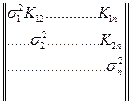
Корреляционная матрица нормированная

Чем больше значимость ошибок второй группы, тем боль­ше значение коэффициента корреляции.

Рассеивание при стрельбе очередями вызвано разбросом траектории каждого отдельного выстрела (или ошибками каждого отдельного выстрела в очереди), а также ошибками, возникающими из-за влияния предыдущих выстрелов па по­следующие.

Числовые характеристики рассеивания при стрельбе оче­редями можно получить только на основании специальных стрельб. Характерным для картины рассеивания на плоскости при стрельбе очередями является то, что можно выделить рассеивание первых, вторых, третьих, и т.д. выстрелов.

обработкой результатов стрельб получают нормированные корреляционные матрицы отдельно по координатам x и z, т.е.

=

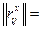
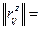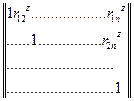
При решении большинства практических задач значения коэффициентов корреляци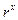и и 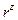мало отличаются друг от друга, поэтому значение коэффициента 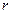можно определить по

формуле 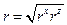, где r^x, r^z, в свою очередь, могут быть определены как осредненные значения:

,

.

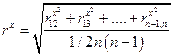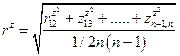Законы поражения целей обычно рассматриваются применительно к двум типам снарядов: ударного и дистанционного. Ударные снаряды поражают цель, при непосредственном в нее попадании, а дистанционные могут поражать цели и при разрыве снаряда на некотором расстоянии. Для оценки эффективности поражения цели недостаточно располагать только характеристиками рассеивания снарядом, необ­ходимо также знать и характеристики уязвимости цели. При стрельбе ударными снарядами уязвимость цели определяется функцией 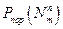(закон поражения цели), являющейся условной вероятностью поражения цели при условии попада­ния в нее 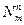снарядов. При стрельбе снарядами дистанционного действия уязвимость цели зависит от координат x и z точки разрыва снаряда.

В общем виде координатный закон поражения есть функция координат точек разрыва снарядов, взятых относительно

цели:

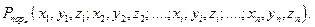
При независимости выстрелов и отсутствии накопления

ущерба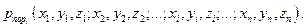

При независимости выстрелов и отсутствия накопления ущерба

.

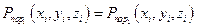Тогда 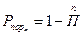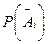, где 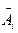--непоражение цели при разрыве снаряда в точке с координатами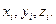

Для вычисления функции 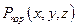для снарядов осколочного действия используют данные опытов — подрывов снарядов в специальной мишенной обстановке и в бронекамере. В результате серии подобных опытов в зависимости от углов разлета определяют весовые данные осколков, их ко­личество н начальные скорости.

Снаряды ударного действия поражают цель при непосред­ственном попадании. Поэтому для такого типа снарядов закон поражения рассматривают в зависимости не от координат точек попадания, а от числа попавших снарядов в цель 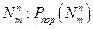. Очевидно: 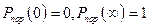. Число попаданий, при котором цель поражается, является случай­ной величиной 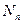. Числовой характеристикой закона пораже­ния является среднее необходимое число попаданий

.

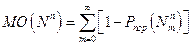При допущении отсутствия накопления ущерба

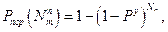
где 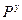— вероятность попадания в уязвимый отсек. Вероятность поражения цели определяется:

— для ударных снарядов

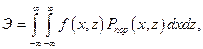
где f(x, z) —закон рассеивания снарядов;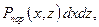

где f(x,z)-- закон поражения цели;

— для дистанционных снарядов

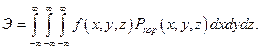
Рассмотрим вероятность поражения цели при нескольких случаях стрельбы:

а) одним ударным снарядом:

,

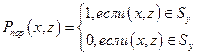где 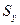--уязвимая площадь цели. Тогда

;

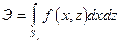б) очередью при n независимых выстрелах:

гипотезы: вероятности выполнения

гипотез:

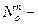в цель не попало ни одного снаряда,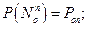

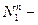в цель попал один снаряд,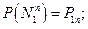

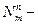в цель попало 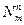снаряда, .

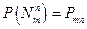Соответствующие вероятности поражения цели

Тогда но формуле полной вероятности (формуле Колмогорова)

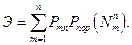
Формулу Колмогорова можно представить в другом виде:

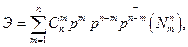
где p — вероятность попадания в цель при одном выстреле;

p=1-p -- вероятность непопадания в цель при одном выстреле;

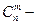число сочетаний из n по m.

В каждом случае, если для поражения цели достаточно одного попадания, т. е.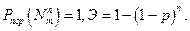

в) очередью при зависимых выстрелах:

пусть событие 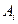— попадание снаряда в цель при i-м выстреле

тогда

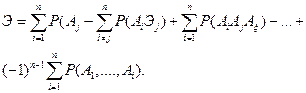
Используя выражение, характеризующее зависимость между выстрелами,

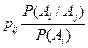
для независимых выстрелов р= 1, так как в этом случае

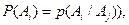можно выражение для Э записать ви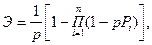де

где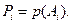

Существуют также различные приближенные зависимости для определения вероятности поражения цели. Так, при стрельбе одним дистанционным снарядом

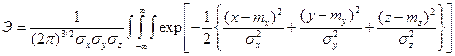
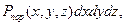
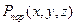определяется соотношением

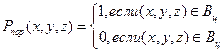
Тогда

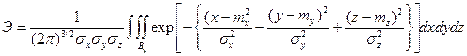
Здесь 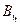--эллипсоид равной плоскости, уравнение которого

.

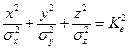После преобразований тройной интеграл приводится к виду

.

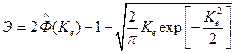В рамках традиционной теории стрельбы рассчитывается и расход выстрелов на поражение нелеп. Результатами этих расчетов пользуются для приближенной оценки ожидаемых затрат на поражение цели при решении задач проектирова­ния операционными методами.

Так, например, расход снарядов на поражение танка мо­жет быть вычислен с помощью формулы

,

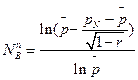где 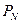— средняя вероятность поражения цели;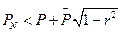

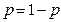; р — вероятность поражения танка при одном выстреле; г — коэффициент корреляции выстрелов;

; ; .

.

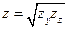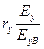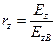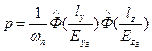где 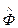табулированная функция 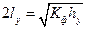; 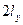и 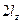— приведенные размеры цели; , 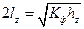; 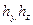— вертикальные и горизонтальные размеры цели (для танка 3,6 и 2,8); 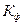--коэффициент фигурности цели, т.е. отно­шение площади цели к площади описанного прямоугольника со сторонам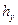и и 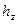(для танка — 0,85); 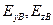—средин­ные ошибки выстрела.

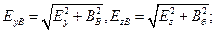
где 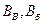--характеристики рассеивания снарядов;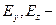

характеристики систематических ошибок выстрелов;

3.4. Внешняя модель функционирования артиллерийского комплекса.

Для построения внешних моделей функционирования артиллерийских систем, кроме результатов теории стрельбы, используются математические методы описания процессов, характеризующих динамику боевых действий. Поток выстрелов. При исследовании динамики боевых действий последовательность выстрелов, осуществляемых каждой единицей, участвующей в бою, удобно представлять как поток случайных событий.

Математическое описание потока выстрелов определяет математический аппарат для описания процессов боевых действий. При этом наиболее эффективным оказывается применение теории марковских процессов.

Краткие сведения из прикладной теории марковских случайных
процессов с непрерывным временем и дискретными
состояниями. Любой случайный процесс может быть представлены как марковский. Представление процесса функционирования всех средств системы в виде марковского процесса с конечным числом состояний и непрерывным временем дает возможность привлекать для исследования эффективности систем хорошо разработанный аппарат обыкновенных диффе­ренциальных уравнений.

Рассмотрим процесс (систему) Y(t), который в любой мо­мент времени может находиться в одном из своих состояний: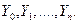

Это дискретный случайный процесс, причем, если 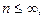то это процесс конечный (счетный).

Пусть событие заключается в том, что 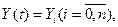а вероятность этого событии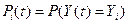

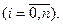
Тогда в любой момент времени t выполняется условие нормирования 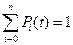— первое свойство марковского процесса.

Одна из основных задач исследования состоит обычно в отыскании вероятностей 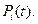В качестве допущения обычно считается, что переход из состояния в состояние происходит скачком (мгновенно). Тогда рассматриваемый процесс может быть представлен как блуждание некоторой точки по своим возможным состояниям.

Характеристикой процесса является также 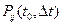— условная вероятность того, что в момент 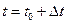система будет в состоянии 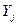, если в момент 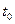она была в состоянии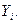

Дискретный случайный процесс называется марковским, если вероятность 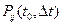зависит только от указанных в обозначении вероятности параметров: в каком состоянии 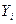была система в момент времени 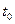и в какое состояние 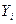система должна попасть в момент 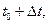и не зависит от того, в каких состояниях процесс находился до момента .

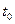Второе свойство марковского процесса:

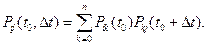
Марковским случайным процессом с непрерывным време­нем называется процесс, у которого переход из одного состоя­ния 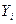в другое, соседнее состояние 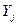, возможен в любой мо­мент времени t. Марковские процессы с непрерывным временем тесно связаны с Пуассоновскими потоками. Можно до­казать утверждение: если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими, то случайный процесс, протекающий в системе, будет марковским с непрерывным временем (пуассоновский процесс:

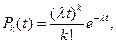где—интенсивность потока.

Рассмотрим простейшую систему, состоящую из двух состояни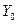й и 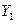, которая может переходить только из 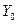в 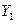под воздействием пуассоновского потока событий с интенсивностью 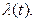Граф такой системы представлен на рис. 3.10. Для рассматриваемого случая имеет место дифференциальное уравнение для вероятности нахождения системы в состоянии 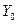(или вероятности невыхода из системы Y₀):

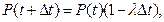
где 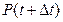--вероятность невыхода

из состояния 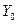за время ;

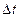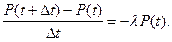
Переходя к пределу, получим дифференциальное уравнение для P(t):

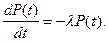
В случае пуассоновских потоков событий, переводящих систему из состояния 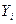в состояние 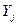, исчерпывающей характеристикой марковского случайного процесса, имеющего (n+1) состояний 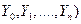, является квадратная матрица интенсивностей пуассоновских потоков 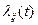при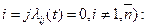

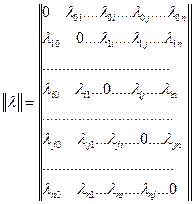
Система дифференциальных уравнений для вероятностей состояний:

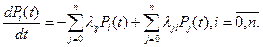
Решение этой системы дифференциальных уравнений — решение задачи Коши, которое в данных условиях существует. Решение такой системы уравнений легко реализуется на ЭВМ.

Рассмотрим частный случай: простейший марковский процесс, у которого матрица интенсивностей простейшая, т.е. все элементы матрицы--постоянные величины ( 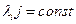). Это означает, что все потоки, переводящие систему из состояния в состояние —простейшие (т.е. обладают свойством однородности и ординарности).

При исследовании таких систем дифференциальных уравнений применяется операторный метод решения дифференциальных уравнений для отыскания вероятностей состояний 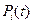.Используется преобразование по Карсону—Хэвисайду, изображение которого имеет вид

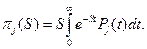
В этом случае система дифференциальных уравнений пре­вратится в систему алгебраических уравнений для изображе­ний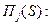

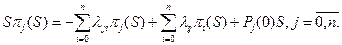
Определив неизвестные 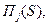по формулам обращения находятся искомые

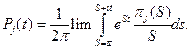
При стационарном режиме, когда 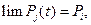вёроятности отыскиваются из системы линейных однородных алгебраических уравнений:

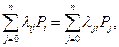
откуда

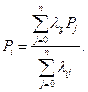
Характеристики случайных процессов гибели и размножения Это дискретные марковские случайные процессы, множество состоянии которого ( 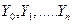) ставится в однозначное соответствие с рядом целых неотрицательных чисел 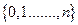и для любого состояния этого процесса (кроме граничных 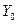и 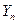) соседними могут быть только те, индексы которых отличаются на величину ±1 (рис. 3.11). На рисунке:

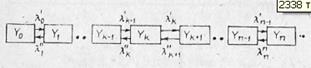
Рис. 3.11. Граф состояний процесса гибели и размножения

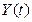--скачкообразная случайная функция,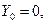 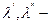интенсивности перехода (соответственно размножения и гибели).

Существуют: процесс чистого размножения 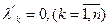и процесс чистого гибели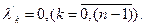

Определим 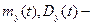математическое ожидание и дисперсию числа единиц вооружения в строю в момент t.

Пусть 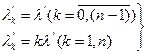--процесс накопления техники одного вида,

где 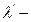интенсивность производства вооружения, 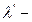интенсивность выхода из строя одной единицы техники, 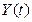— число единиц вооружения в строю в момент t.

Система дифференциальных уравнений для вероятностей

состояний:

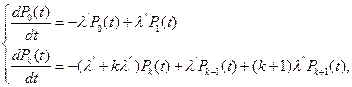
где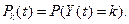

Умножим второе уравнение на k и просуммируем по всем k:

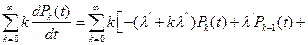
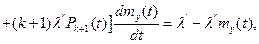
где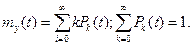

При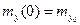

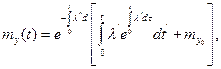
При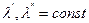

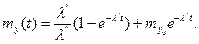
При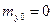

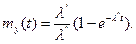
Если уравнение умножить на k² и просуммировать, то получим

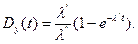
Можно убедиться, что

.

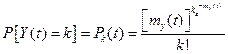Полученные выражения говорят о пуассоновском законе распределения (для распределения Пуассона .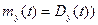

Рассмотренный теоретический аппарат используется для описания боевых действий и построения моделей боя.

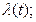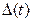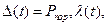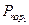Плотность потока выстрелов (рис. 3.12). На рисунке обозначено —поток выстрелов, характеризующийся интенсивностью * *— поток успешных выстрелов с интенсивностью . Очевидно, что где — вероятность поражения цели одним выстрелом.

Простейшая модель боя. Имеются две противодействующие группировки. Каждая состоит из однородных между собой боевых единиц. Первая группировка из 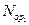, единиц, вторая из 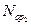единиц.

Пусть любая боевая единица, пока она не поражена, производит случайный пуассоновский поток выстрелов с некоторой средней скорострельностью; любая боевая единица первой

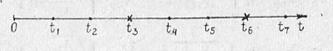
Рис. 3.12. Поток выстрелов

группировки может стрелять по любой из второй и, наоборот, одним выстрелом нельзя поразить больше одной цели; если цель поражена мгновенно, огонь переносится на другую цель.

Используются обозначения: 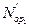— среднее число боевых единиц первой группировки, сохранившихся непораженными к моменту t; 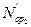— среднее число боевых единиц второй группировки, сохранившихся непораженными к моменту t; 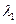--средняя скорострельность (число выстрелов в единицу времени) для одной боевой единицы первой стороны; 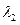— средняя скорострельность для одной боевой единицы второй стороны;

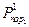—вероятность, с которой поражает цель один выстрел орудия первой стороны; 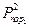— вероятность, с которой поражает цель один выстрел орудия второй стороны,

Тогда 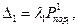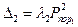— пуассоновские потоки успешных выстрелов. За малый промежуток времени 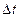наблюдаются изменения:

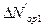-среднего числа боевых единиц первой группировки;

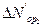среднего числа боевых единиц второй группировки

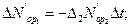
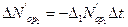
Через предельный переход получаются уравнения динамики боя:

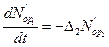---уравнения Ланчестера 2-го рода.

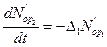
при t=0: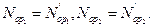

Решение системы при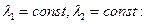

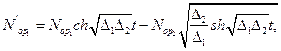
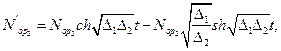
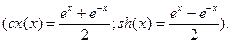
Рассмотренная модель динамики средних, оперирующая математическими ожиданиями числа участвующих в бою единиц, построена для простейшего случая: противоборствующие группировки состоят из определенного количества однотипных единиц, характеризуемых скорострельностями и вероятностями поражения единицы противника. Такая модель обладает достаточной точностью при сравнительно большом числе единиц (>10).

При новых обозначениях 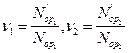система уравнений имеет вид

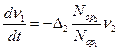
при t=0,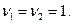

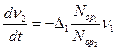
Здесь 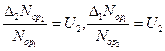— характеристики интенсивности воздействия.

Тогда

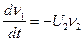
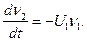
Решение системы уравнений при этом запишется как

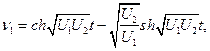
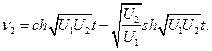
При обозначении 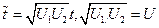решение получает вид

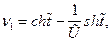
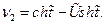
При 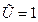(силы сторон равны)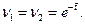

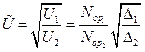— характеризует преимущество первой стороны над второй.

Если 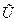>1, то победит первая группировка, если 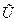<1, победит вторая группировка.

При обозначении 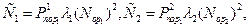время окончания боя

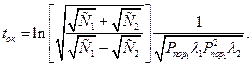
Количество сохранившихся единиц более сильной стороны

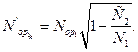Условие победы >

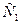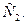
Несмотря на кажущуюся простоту, эта модель дает возможность учесть влияние многих факторов. В частности, если | рассматривается противотанковая артиллерия и танки, то можно учесть влияние скорострельности, точности и кучности стрельбы (через 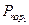), размеры и степень защищенности противотанковых комплексов (через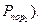

Суммарные затраты на поражение группировки танкой в этом случае

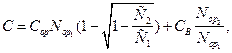
где 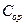— стоимость орудия; 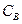— стоимость выстрела.

Пример. Подразделение из восьми противотанковых пушек, любая из которых обладает скорострельностью 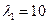в/мин и вероятностью поражения танка 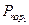= 0,8, противостоит группировке в десять танков, каждый из которых обладает практической скорострельностью 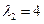в/мин и 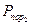= 0,4. Определить исход боя и суммарные затраты противотанковой группировки, если стоимость орудия 1000 усл. ед., стоимость выстрела 10 усл. ед.

Решение. 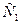= 10 * 0,8 * 8² = 512, 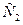= 4 *4* 10²== 160 >

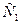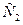> , таким образом, противотанковая группировка выигрывает бой.

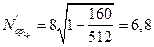орудий — число сохранившихся противотанковых пушек.

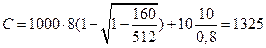усл. ед.

Если бы противодействие противника не учитывалось, то 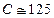усл. ед. всего. Модель может усложняться за счет учета влияния маневренности, разведки и т. п.

При более полном описании боевых действий необходимо рассмотреть по возможности все физические состояния, позволяющие учесть все основные факторы, влияющие на эффективность функционирования системы.

Для разработки модели системы, описываемой уравнением для марковского процесса с непрерывным временем и дискретным числом состояний, необходимо определить основные типы средств, входящих в систему; основные физические состояния; значения интенсивностей; начальные условия для интегрирования, а также составить систему дифференциальных уравнений, описывающую вероятности состояний системы в процессе функционирования.

В качестве примера модели, учитывающей маневренность арткомплекса, рассматривается система, изображенная на рис. 3.13.

Состояния данной системы:

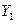— выдвижение артсистемы из выжидательного района (BP) или перемещение па новую огневую позицию (ОП);

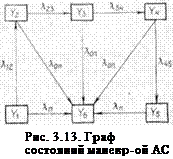
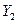— перевод артсистемы из походного положения в боевое (развертывание);

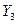— выполнение огневой задачи;

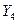— перевод из боевого положения в походное (свертывание) ;

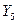— перемещение с заданной ОП на другую (или в ВР);

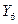— переход в состояние Поражения;

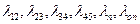— интенсивности перехода из состояния в состояние ( 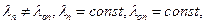так как цель точечная).

Каждое состояние артсистемы характеризуется своей ве­роятностью 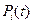Вероятности 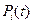определяются системой уравнений Колмогорова:

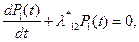
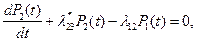
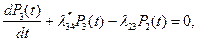
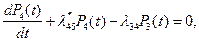
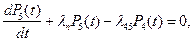
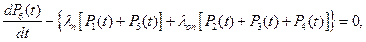
где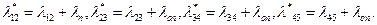

Начальные условия:

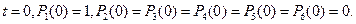
Решение системы может быть получено аналитически (в виде суперпозиции экспонент, например: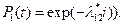

Среднее время пребывания артсистемы и i-м состоянии при наличии противодействия противника может быть определено как

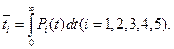
Анализируя результаты решения (например, значения 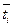), можно определить направления улучшения характеристик артсистемы. Одним из резервов повышения непоражаемости является конструктивное усовершенствование артсистемы в направлении уменьшения временных характеристик 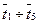(например, уменьшение времени 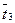за счет механизации и автоматизации процессов подготовки и выполнения огневых задач).

В качестве примера модели, учитывающей влияние разведки на функционирование основных средств системы, рассматривается марковский процесс двусторонних боевых действий группировок, каждая из которых состоит из однородных боевых средств (подвижных). 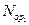— общее число средств первой стороны, 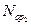— о