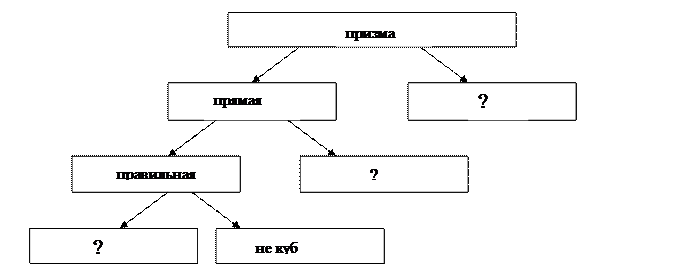
Нахождение основных элементов призм.
Цель работы
Научиться изображать призму и находить длину основных элементов, используя определение и свойства призм
Ход работы
Вариант
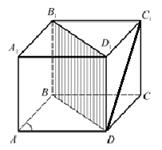
2.1.1 Сделайте рисунок
_____________________________________________________________ обозначьте её и запишите:
- вершины,
- основания,
- боковые рёбра,
- боковые грани,
- проведите одну из диагоналей её боковой грани и выпишите её,
- проведите две диагонали призмы и выпишите их,
- постройте одно диагональное сечение и выпишите его.
2.1.2 Дан прямоугольный параллелепипед
___________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.3 Дана правильная четырёхугольная призма
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.4 Дана правильная четырёхугольная призма
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.5 Дана правильная треугольная призма
___________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.6 Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.7 Дана прямая четырёхугольная призма, в основании которой лежит ромб
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
 |
2.1.8 Дана прямая четырёхугольная призма, в основании которой лежит параллелограмм
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.9 Дана прямая треугольная призма, в основании которой лежит равнобедренный треугольник
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.10 Дано:
_________________________
_________________________
_________________________
Найти:
_________________________
_________________________
Допуск к работе
2.2.1  Заполните пропуски
Заполните пропуски
2.2.2 Заполните таблицу
| Название | Основание | Взаимное расположение боковых рёбер и основания |
| Правильная треугольная призма | Правильный треугольник | Боковое ребро перпендикулярно основанию |
| Правильная четырёхугольная призма | ||
| Прямой параллелепипед | ||
| Прямоугольный параллелепипед | ||
| Наклонный параллелепипед | ||
| Прямая треугольная призма | ||
| Куб | ||
| Прямая четырёхугольная призма |
2.2.3 Дана правильная четырёхугольная призма АВСДА1В1С1Д1. Запишите теорему Пифагора для треугольника В1ДВ.
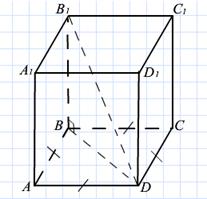
_____________________________
 |
2.2.4 Заполните таблицу
| Фигура | Рисунок | Площадь |
| Равносторонний треугольник | 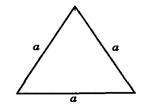 | |
| Ромб | 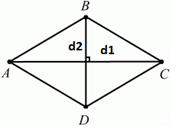 |
2.2.5 Дана правильная четырёхугольная призма, сторона основания которой равна 5, а высота 10. Заполните пропуски:
1) Площадь основания - _______________
2) Диагональ основания - ______________
3) Площадь диагонального сечения - _____________
4) Диагональ боковой грани - ____________________
2.2.6 Запишите теорему косинусов:
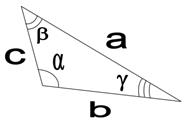
а2 = ___________________________
К работе допускается ______________
Результаты работы
 ПРАКТИЧЕСКАЯ РАБОТА 23
ПРАКТИЧЕСКАЯ РАБОТА 23
Нахождение основных элементов пирамид.
Цель работы
Научиться изображать пирамиду и находить длину основных элементов, используя определение и свойства пирамид
Ход работы
Вариант
2.1.1
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
____________________________________________________________________
2.1.2 В треугольной пирамиде площадь основания равна см2, площадь параллельного сечения см2, расстояние от сечения до вершины пирамиды равно см. Найдите высоту пирамиды.
2.1.3 Основание пирамиды – прямоугольник со сторонами и см; каждое боковое ребро пирамиды равно см. Найдите высоту пирамиды.
2.1.4 В правильной треугольной пирамиде боковое ребро равно см и образует с плоскостью основания угол 0. Найдите сторону основания пирамиды.
2.1.5 В правильной треугольной пирамиде по стороне основания м и боковому ребру м определить площадь сечения, проведенного через боковое ребро и высоту пирамиды.
2.1.6 Длины сторон основания правильной четырехугольной усеченной пирамиды равны и см, длина бокового ребра равна см. Найдите площадь диагонального сечения.
Допуск к работе
2.2.1 SABC - правильная треугольная пирамида, SO - высота пирамиды. Запишите теорему Пифагора для треугольника SAO.
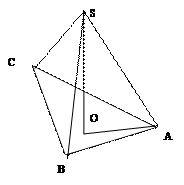
__________________________________
2.2.2 Найдите неизвестный член пропорции 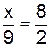
2.2.3 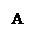 Дан прямоугольный треугольник АВС. Найдите синус угла САВ
Дан прямоугольный треугольник АВС. Найдите синус угла САВ
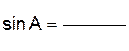
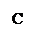

2.2.4 Продолжите утверждение:
А) Если боковые рёбра пирамиды равны, то основание высоты, проведённой из вершины на основание совпадает_______________________________________
____________________________________________________________________
Б) Если все боковые грани пирамиды образую с плоскостью основания равные двугранные углы, то основание высоты, проведённой из вершины на основание совпадает ____________________________________________________________
____________________________________________________________________
В) Апофемой правильной пирамиды называется __________________________
________________________________________________________________________________________________________________________________________
2.2.5 АВСДА1В1С1Д1 – усечённая пирамида. Какой фигурой является четырёхугольник АА1С1С? _____________________________________________
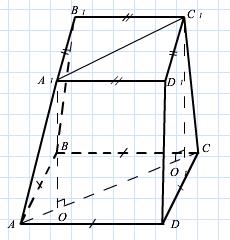
Запишите формулу для вычисления площади этого четырёхугольника

К работе допускается ______________
Результаты работы

 ПРАКТИЧЕСКАЯ РАБОТА 24
ПРАКТИЧЕСКАЯ РАБОТА 24
