Построение графиков тригонометрических функций.

Цель работы

1. 1 Научиться строить графики тригонометрических функций и выполнять преобразование графиков

Ход работы

Вариант

Постройте графики функций:

2.1.1.	2.1.3
2.1.2	2.1.4
2.1.5

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 11

Решение тригонометрических уравнений.

Цель работы

1. 1 Научиться решать простейшие тригонометрические уравнения;

1.2 Научиться решать тригонометрические уравнения, приводимые к простейшим;

1.3 Научиться решать однородные тригонометрические уравнения первой и второй степени.

Ход работы

Вариант

Решите уравнения:

2.1.1.	2.1.6.
2.1.2	2.1.7
2.1.3	2.1.8
2.1.4	2.1.9
2.1.5	2.1.10

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 12

Последовательности. Способы задания и свойства числовых последовательностей.

Цель работы

1.1 Научиться вычислять n-ые члены последовательностей, заданных различными способами;

1.2 Научиться изображать последовательности различными способами;

1.3 Научиться вычислять пределы числовых последовательностей.

Ход работы

Вариант

1) Найдите знаменатель и сумму геометрической прогрессии (b_n), если

b₁ = , b₂ = .

2) Задайте последовательность аналитически и найдите первые пять членов этой последовательности: каждому натуральному числу ставится в соответствие ______________________________________________________________________________________________________________________________________________

3) По заданной формуле n-го члена вычислите пять первых членов последовательности (у_n):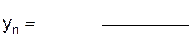

4) Выпишите первые пять членов последовательности, заданной рекуррентно:

х₁ = , x_n = . Постройте график последовательности.

5) Найдите сумму первых трёх членов последовательности

6) Выясните, является ли число b членом последовательности b_n и укажите номер n

b_n = 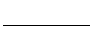, b =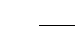

7) Укажите, начиная с какого номера все члены последовательности (х_n) будут меньше заданного числа А?

, A =

8) Выпишите первые пять членов последовательности. Изобразите точками на числовой прямой члены последовательности. Найдите, если возможно, отрезок или интервал, которому принадлежат все члены последовательности. Является ли данная последовательность ограниченной сверху, ограниченной снизу, или ограниченной.

Вычислите пределы:

9)	10)
11)	12)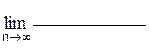
13)	14)
15)

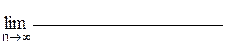Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 13

Нахождение производных функции.

Цель работы

Научиться вычислять производную функции, используя таблицу производных и правила

дифференцирования

Ход работы

Вариант

Найдите производную функции с помощью формулы :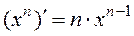

1)

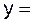
Найдите производную функции, преобразовав по свойству :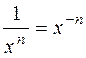

2)

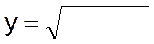
Найдите производную функции, преобразовав по формуле :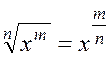

3)

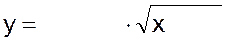4)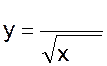

Найдите производную функции, применив правило :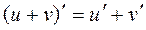

5)

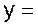6)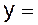

Найдите производные сложных функций :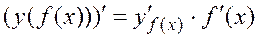

7)	8)
9)	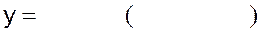10)
11)	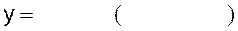12)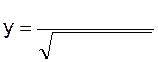
13)

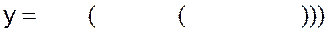Найдите производные, применив правило :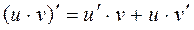

14)	15)
16)

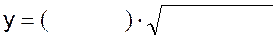17)Вычислите значение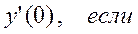

Найдите производные, применив правило :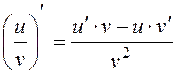

18)	19)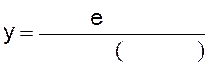
20)Вычислите значение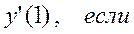

Результаты работы

ПРАКТИЧЕСКАЯ РАБОТА 14

Построение графиков функции с помощью производной.

Цель работы

Научиться исследовать функцию с помощью производной и строить по результатам исследования график

Ход работы

Вариант

Исследовать функцию и построить её график:

2.1.1

2.1.2

2.1.3

2.1.4

Результаты работы

3.1

y =

1) Область определения функции D(f) =

2) Четность, нечетность функции

f(-x) =

_____________________________________________________________________________________

3) Точки пересечения графика функции с осями координат

А) с осью ОХ ( у=0)

Б) с осью ОУ ( х=0)

4) Первая производная: y’ =

5) Стационарные точки: (y’ = 0)

____________________________________________________________________________________

6) Промежутки монотонности (возрастания, убывания)

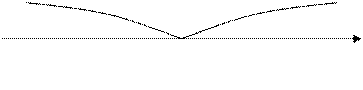
Возрастает _______________________

Убывает __________________________

7) Экстремумы:

Максимум: x_max = y_max =

Минимум: x_min = y_min =

8) Вторая производная у ‘’ =

Выпукла ____________________

Вогнута _____________________

9 ) График функции:

х
у

3.2

y =

1) Область определения функции D(f) =

2) Четность, нечетность функции

f(-x) =

_____________________________________________________________________________________

3) Точки пересечения графика функции с осями координат

А) с осью ОХ ( у=0)

Б) с осью ОУ ( х=0)

4) Первая производная: y’ =

5) Стационарные точки: (y’ = 0)

____________________________________________________________________________________

6) Промежутки монотонности (возрастания, убывания)

Возрастает _______________________

Убывает __________________________

7) Экстремумы:

Максимум: x_max = y_max =

Минимум: x_min = y_min =

8) Вторая производная у ‘’ =

Выпукла ____________________

Вогнута _____________________

9 ) График функции:

х
у

Наши рекомендации Построение графиков функций Построение ряда чисел. Вычисления со строкой формул. Сводные таблицы. Построение расчетных таблиц, графиков функций. Консолидация данных» Тема: Применение математических, статистических и логических функций, построение графиков функций в табличном процессоре MS Excel’2000/2003 Тема: Применение математических, статистических и логических функций, построение графиков функций в табличном процессоре MS Excel’2000/2003. Построение графиков функций. Mathcad допускает создание новых функций от одного и более аргументов Построение графиков функций Построение графиков функций Построение графиков функций Исследование функций и построение графиков функций. Построение графиков функций. Задание 7.На новом листе Графики функций выполнить задания ← Предыдущая страница | Следующая страница →