The nominative with the infinitive construction (complex subject).
FOR +INFINITIVE.
Ex 1. The Objective with the Infinitive Construction (Complex Object)
a) With the verbs: to want, to wish, to like, to love, to prefer and to desire.
Example. I want you to participatein the experiment.
Я хочу, чтобы вы участвовали в этом эксперименте.
1. The teacher wanted his students to learn as quickly as possible.
2. I prefer you to call me by my first name.
3. He would like me to change my mind.
4. They wished the article to be published next month.
5. We want one of her best students to be granted a scholarship.
b) With the verbs: to order, to ask, to tell, to advise, to allow, to forbid and to cause.
Example.Did he allow you to take thedictionary?
Он разрешил тебе взять словарь?
1. Professor permitted us to be helped with the solution of the problem.
2. We don’t allow students to cheat or talk to each other during exams.
3. I advise you to look for a new job.
4. They ordered us to finish our projects until Tuesday.
5. She asked everybody not to use the office photocopier.
c) With the verbs: to think, to believe, to mean, to admit, to expect, to suppose, to consider, to know and to prove.
Example.. She knows Yorkto be a historic city in England with many ancient buildings.
Она знает, что Йорк исторический город в Англии, где много древних зданий.
1. In the future they suppose students to use computers instead of text books.
2. We expect you to be able to account for this mistake.
3. I suppose the sense of beauty to be very personal and subjective.
4. We consider the algebraic language of analytic geometry to have bothadvantages and disadvantages.
5. They know maths to provide basic tools for computer science.
Complex Object + with Infinitive without ‘to’
d) With the verbs: to see, to feel, to watch, to notice and to hear.
Example.Do you feel the Earth move?
Вы чувствуете, как Земля движется?
1. We cannot see a point move along the line.
2. We both heard him say that I was leaving.
3. The students watched their teacher draw two perpendicular lines.
4. Nobody heard him complain about being overworked.
5. He noticed them walk out of the building together laughing and joking.
e)With the verbs: to let, to make (заставлять), to have.
Example.Let him stay up late tonight.
Разрешите ему позже лечь спать сегодня вечером.
1. She made him accept full responsibility for the accident.
2. Shall I have my secretary send you the details?
3. Let him solve this cubic equation in terms of substitution.
4. You can’t make her come on time. She is not punctual.
5. The teacher let his students use a calculator in the test.
Ex.2. Translate these sentences into English using Complex Object.
1. Мне бы хотелось, чтобы эта задача была решена другим способом.
2. Декарт (R. Descartes) хотел, чтобы методы, используемые математиками были обобщены и расширены.
3. Гений и трудолюбие Эйлера (L. Euler) позволили ему стать самым плодовитым (prolific) математиком за всю историю ее существования.
4. Ученые полагают, что эта теория может стать основой для получения многих новых идей в науке.
5. В соответствии с постулатом геометрии мы знаем, что точка M и направляющий вектор q определяют прямую линию L.
6. Сегодня мы заставляем компьютер решать сложные задачи, запоминать непростые цепочки операций, рисовать графики и выполнять другую полезную и нужную работу.
Ex 3. The Nominative with the Infinitive Construction (Complex Subject)
Subject + /predicate/ + to – Infinitive.
a) With the predicate in the passive voice: to see, to believe, to suppose, to expect, to think, to know, to announce, to report and to say.
Example. He is believed to be a great authority on the subject.
Считают, что он крупный специалист по этой теме.
1. Unless stated otherwise, curves are always assumed to be simple, that is they do not intersect.
2. The binary system is expected to be appropriate to the nature of an electronic machine.
3. The Earth is known to rotate and as a result it has the shape of a ball.
4. When the limits of integration to be performed are stated, the integral is said to be definite.
5. Lack of oxygen is believed to make people lose health.
b) With the predicate in the active voice: to seem, to appear, to happen, to chance, to prove, to turn out.
Example. His method proved to bethe only possible one. Оказалось, что его метод является единственно возможным методом.
1. I chanced to be passing when she fell and hurt herself.
2. Computers do not seem to be able to use their memories in the way human beings use theirs.
3. The fundamental concepts of many branches prove to have been suggested by physical experiments.
4. This function, whose graph is a line, appears to be classified as a linear function.
5. The graph turned out to be drawn without picking up the pencil.
c) The predicate to be + adjective (likely, unlikely, sure, certain).
Example. The computer is not likely to make such mistakes.
Маловероятно, что компьютер делает такие ошибки
1. When the quantity is a constant multiple of another quantity, they are certain to be directly proportional to one another.
2. He is unlikely to know what a discontinuous function is.
3. Such an effect is likely to be the result of an experimental error.
4. The traditional role of science seems to make people healthy and the world a brighter place to live in.
5. Any quantity associated with a curve (e.g. the coordinates of a point on a curve, the length of a tangent to the curve) are sure to represent a function.
Ex.4. Translate these sentences into English using Complex Subject.
1. Маловероятно, что этот план утвердят на собрании.
2. Несомненно, что они выбрали другую систему координат.
3. Оказывается, что если значение одной тригонометрической функции А будет дано, то все остальные функции будут однозначно определены.
4. Предполагали, что полученные данные будут точными.
5. Говорят, что такое уравнение (х+1)2 + y2 = - 4 не имеет решения и описывает мнимую окружность.
6. Известно, что такие поверхности как сфера или эллипс характеризуются квадратными уравнениями.
7. Несомненно, что значение математики непрерывно возрастает.
Ex. 5. Replace the Object Clause with Complex Object. See the models.
Example 1.I would like to draw both axes (she).
She would likeme to draw both axes.
1. The astronomers wish to locate this distant object in the sky. (they)
2. We expect to find the equation of the ellipse with foci at the
points (0,4). (he)
3. We want to use analytic methods to find the equation of loci. (she)
4. I expect to prove the advantages of this system of notation in this
particular case.( you)
5. He wants to interpret these facts correctly. (they)
Example 2.Scientists suppose that non-Euclidean geometries liberated the science.
Scientists suppose non-Euclidean geometries to have liberated the science.
1. We know that P. Fermat and R. Descartes came to develop analytic geometry almost simultaneously.
2. We believe that Cybernetics is the twentieth century Queen of sciences.
3. I know that more and more prospective employees take lie-detector tests.
4. Programmers assume that community networks, like public libraries, serve citizens and society.
5. He believed that concepts of importance in science had come to men with great difficulty.
Ex.6. Change the sentences with Complex Object to the sentences with Complex Subject.
Example.We know the concepts of gravity, of energy and of limitless space to have takenyears to develop.
The concepts of gravity, of energy and of limitless spaceare known to have taken years to develop.
1. They believe men of genius to be required to express the concepts of importance in science.
2. We expect the best mathematical proofs to be short and direct.
3. I believe CD-ROM to be going to replace printed books and newspapers.
4. She supposes him to understand such simple sentences.
5. My science adviser expects me to take part in the international conference.
For + Infinitive Construction
For + object + to - Infinitive
(Can be used in different functions).
a) The Subject(подлежащее).
It’s for you to decide what university to choose.
Тебе решать, какой университет выбрать.
b) The Predicative (именная часть сказуемого).
The best thing to do is for us to come to an agreement.
Лучшее, что мы можем сделать, это прийти к соглашению.
c) The Object (дополнение).
The conference called for the government to take measures against growing unemployment.
Конференция потребовала, чтобы правительство приняло меры против растущей безработицы.
d) The Adverbial modifier of purpose(обстоятельство цели).
For the expected results to be obtained, we have to use the computations.
Чтобы получить ожидаемые результаты, мы должны использовать эти вычисления.
e) The Attribute (определение).
The speaker proposed a new method for the experiment to be carried out successfully.
Выступающий предложил новый метод для успешного выполнения эксперимента.
Ex. 7. Translate these sentences into Russian.
1. I must find somewhere for him to practice his English.
2. It’s important for the meeting to start at eight a.m.
3. It seems unnecessary for him to start his work this week.
4. It was a real shame for them not to have won after all their attempts.
5. For us to fail the experiment now would be a disaster.
6. Two conditions must be met for the phenomenon to occur.
Ex. 8. Translate these sentences into English using the for + Infinitive Construction.
1. Математикам важно помнить, что строгий метод легче понять.
2. Возможно, что фигура будет иметь больше, чем одну ось симметрии.
3. Чтобы этот закон выполнялся, необходимо соблюдать два условия.
4. Потребуется больше экспериментальной работы, чтобы мы смогли объяснить это явление.
5. Необходимо, чтобы финансовые сделки (transactions) в Интернете были безопасны. Однако существует определенная проблема.
6. Жизненно важно (vital), чтобы существовала хорошая система общественного транспорта в больших городах.
Ex. 9. Make up sentences about the mathematicians using the same models with any of the given verbs: alleged, believed, claimed, considered, known, reported, said, supposed, thought and understood.
Model.1. Marie Curie was thought to be the greatest scientist of her generation.
2. She is known to have succeeded where all others had failed.
3. It used to be said that she owed her success to her husband Pierre.
L. Euler - a great geometer of 18th century;
- worked at the St. Petersburg Academy;
- dealt with analytic functions;
- was the first to solve the equation in three variables;
- his greatest discovery was the calculus of quaternion (кватернион).
P. Fermat - the greatest “amateur in the history of mathematics”;
- enjoyed classical literature, wrote verses;
- inventor and discoverer of coordinate geometry;
- the proofs of his famous theorems are not obtained.
- his books were not lost after his death.
W.P. Hamilton - one of the greatest scientists;
- at the age of 21 submitted to the Royal Irish Academy a paper “A Theory of Systems of Rays”;
- when an undergraduate was elected to the chair of Professor of Astronomy at Trinity College;
- devised math tools for the exploration of physical space;
- thanks to his mathematical tools the subject of vector analysis appeared.
Ex.10. Rewrite each sentence, beginning as shown. Do not change the meaning and use the word given.
1. Some people can’t remember historical dates.
For some people … (impossible)
2. It goes without saying, we’ll be very happy to accept your invitation.
We are sure … (delighted)
3. You must remember to check your work through for mistakes.
It is … (essential)
4. I think they were very much pleased with my work.
I expect them … (extremely)
5. There’s no doubt, her business was successful, as she was a very capable person.
Her business is certain … (gifted)
6. To make notes before you start writing is very important.
For you … (essential)
7. My teacher has checked my answers for slips of the pen.
I’ve had … (carefully)
8. He normally stays up late on Saturdays.
To stay up late … (normal)
9. I had to write my name in block capitals.
They made … (clearly)
10. It’s hard for her to live up to her mother’s expectations.
She finds … (difficult)
Ex.11. Complete the answers to the questions. For some of them use the words or phrases suggested.
1. What’s the Latin version of the name R. Descartes?
-We know … (Renatus Cartesius)
2. Who is considered to be the founder of analytic geometry?
- Descartes and Fermat …
3. What does the name analytic mean?
- Analytic geometry is certain to be …
(general method of geometry; the basis of all modern applied maths)
4. What is the heart of Descartes’ and Fermat’s idea concerning studying geometric figures and curves?
- To each curve there belongs an equation, and it is expected …
(points of the curve, no other points, to describe)
5. Was Descartes the original creator of rectangular coordinates?
- No, he wasn’t. But it often … (to refer to as, Cartesian)
- It’s due to his …
(to introduce, his coordinate geometry, innovations, to improve algebraic notation)
6. Who was the first to introduce the concepts of a variable and a function?
- Everybody knows … .
7. What allowed negative numbers to become legitimate in maths as directed ordinates?
- The rule of signs and his coordinate geometry appear … .
8. Who devised the method of plotting graphs with x and y coordinates?
- French mathematicians Descartes and Fermat are supposed … .
9. To Descartes maths served to solve philosophical and scientific problems and master nature, didn’t it?
- Yes, he expected maths … .
10. How can you characterize his life and his philosophy?
- In contrast to Fermat’s life his life is said … .
(to devote, thinking about the nature of truth and the physical structure of the universe)
Pre-Reading Activity
Guess the meaning of the following words:
function (n) ['fANkSn] formula (n) ['fO:mjulq]
graph (n) ['grxf] distance (n) ['dIstqns]
real (a) ['rIql] temperature (n) ['temprItSq]
condition (n) [kqn'dISn] reflect (v) [rI'flekt]
qualify (v) ['kwOlIfaI] assistance (n) [q'sIstqns]
physical (a) ['fIzIkql] special (a) ['speSql]
coordinate (n) [kou'O:dnIt]
Read and learn the following words:
approach (v,n) [q'proutS] приближаться, подходить; подход
assign (v) [q'saIn] ставить в соответствие
assume (v) [q'sjHm] предполагать, допускать
concept (n) ['kOnsept] логическое понятие
convex (a) ['kOn'veks] выпуклый
correspond (v) ["kOrIs'pOnd] соответствовать
describe (v) [dIs'kraIb] описывать, изображать, начертить
domain (n) [dq'meIn] область (определения)
dimension (n) [dI'menSn] размерность
emerge (v) [I'mWG] появляться, выходить, выяснять
feed (v) ['fJd] подавать, питать
graph (n) ['grxf] диаграмма, график
instance (n) ['Instqns] случай, пример
mapping (n) ['mxpIN] отображение
modify (v) ['mOdIfaI] (видо)изменять, модифицировать
notion (n) ['nouSn] понятие, определение
original (a) [O'rIGInql] первоначальный
obey (v) [q'beI] удовлетворять условиям
qualify (v) ['kwOlIfaI] определять, квалифицировать
regardless (a) [rI'gRdlIs] независимо от, несмотря на
require (v) [rI'kwaIq] нуждаться, требовать
restrict (v) [rI'strIkt] ограничивать, заключать
satisfy (v) ['sxtIsfaI] выполнять, удовлетворять
statement (n) ['steItmqnt] утверждение, формулировка
suitably (adj) ['sjHtqblI] соответственно, подходяще
whereas (cj) [wFqr'xz] тогда как, поскольку
unique (a) [jH'nIk] единственный, однозначный
yield (v) ['jJld] производить, вырабатывать
NOTES
to bear in mind помнить
according to согласно
to refer to …as называть
side by side рядом
by analogy по аналогии
an ordered pair упорядоченная пара
at least по крайней мере
TEXT A
FUNCTIONS AND GRAPHS
The notion of functionis essentially the same as that of correspondence. A numerical-valued function f assigns to each point p in its domain of definitiona single real number f(p) called the value of f at p. The rule of correspondence may be described by a formula such as
f (p)=x2 – 3xy, when p=(x, y)
or by several formulas, such as
f (p) = x when x › y
x2 +y y ≤ x
or by geometric description.
F (p) is the distance from p to the point (4,7)
or even by an assumed physical relationship:
f (p) is the temperature at the point p.
In all of these instances, it is important to bear in mind that the rule of correspondence is the function f, whereas f (p) is the numerical value which fassigns to p. A function may be thought of as a machine into which specific points may be fed, while the corresponding values emerge at the other end.
Real-valued functions are often classified according to the dimension of their domain of definition. If f (p)is defined for all p є S and S is a subset of the plane, then we may write p as (x, y) and f (p) as f (x, y) and refer to f as a function of two real variables. Similarly, when S is a set in 3-space, we may write f (x, y, z) for f (p) and say that f is a function of three real variables. When S is a set on the line, we usually write f (x) and call f a function of one real variable. In all these cases, however, f can still be thought of as a function defined for the single variable point p.
Other cases also arise. A function f may be defined only for points p which lie on a certain curve C in space.
Side by side with the notion of a function as a correspondence or mapping between two sets (e.g. points and numbers), we have the concept of graph. If fis a function of one real variable, the graph of f is the set f points (x, y) in the plane for which y = f(x). If f is a function of two real variables, the graph of f is the set of points (x, y, z) in 3-space for which z = F (x, y). Conversely, it is possible to base the notion of function on that of graph. Let A and B be any two sets, and let E be any set composed of ordered pairs (a, b) with a є A and b є B. By analogy, (a, b) may be called the “point” in a A x B space having coordinates a and b, regardless of the nature of the sets A and B. Any such set E can be called a graph or relation, and those that have the special property of being single-valued are called functions.
Many special properties of a function are reflected in simple geometrical properties of its graph. A function f defined on the line is said to be monotonic increasing if f (x) ≤ f (x')whenever x < x'; this means that the graph of f “rises” as we move along it from left to right. Again, a function of two variables is said to be convex if it obeys the condition
f (p1) + f (p2) ≤ 2 f ;
this says that Σ, the graph of f, is a surface with the property that if A and B are any two points on Σ, their mid – point lies on or below Σ.
Sometimes it is said that equation in x and y defines y as a function of x. This must both be explained and qualified. What is meant is that, given an equation E (x, y) = 0, one is generally able (at least in theory) to “solve for y”, getting y = f (x). Again, solution of the equation for y seldom gives a unique answer, while in writing y = f (x),we require that exactly one value of y corresponds to a given value of x.We must therefore modify the original statement and say that if the function E is suitably restricted, the equation E (x, y) = 0defines a set of functions (possibly just one) such that if f is one of these, then E (x, F (x)) =0for all x in the domain of definition of f. The equation x2 + y2 – 16 =0yields two functions,
f (x) = √ 16 – x2and g (x) = -√16 – x2.
Post-Reading Activity
Ex. 12. Answer the questions on the text:
1. What may the notion of function be compared with? 2. What can the rule of correspondence be described by? 3. In what way are real-valued functions related to the concept of graph? 4. How are the special properties of a function reflected in geometrical properties of its graph? 5. Can it be explained that any equation in x and y defines y as a function of x ?
Ex. 13. Match the English words and word combinations with their Russian equivalents.
| 1. a mapping | a. называться |
| 2. to assign to | b. область определения |
| 3. a domain of definition | c. правило соответствия |
| 4. the rule of correspondence | d. быть монотонно возрастающей |
| 5. to bear in mind | e. помнить |
| 6. to refer to... as | f. допускаемая величина |
| 7. a value assumed | g. упорядоченная пара |
| 8. a function defined | h. определяемая функция |
| 9. to lie on a curve | i. лежать на кривой |
| 10. the concept of graph | j. подчиняться условию |
| 11. an ordered pair | k. без ограничений |
| 12. to be monotonic increasing | l. однозначный ответ |
| 13. to obey a condition | m. первоначальное утверждение |
| 14. without restrictions | n. отображение |
| o. соответственно ограниченный |
| p. понятие графика |
| q. ставить соответствие |
Ex. 14. Replace the Russian words by their English equivalents according to the text.
1. Describe (область определения) of each function f defined below.
2. (Правило соответствия) may be described by a formula.
3. A function f (может быть определена) only for points p, which lie on a certain curve С in space.
4. We must modify (первоначальное утверждение).
5. Real-valued functions are often classified (в соответствии с размером) of their domain of definition.
6. It is important (помнить) that the rule of correspondence is the function f.
7. Many (особые свойства) of a function are reflected in simple geometrical (свойства) of its graph.
8. A function of two variables, (говорят, выпуклая) if it obeys the certain conditions.
Ex. 15. Complete the sentences using the required forms of the verb “to participate” (Infinitive or Gerund):
1.to participate
2.participatein the scientific research
3.participating
a) I had no desire …
b) In fact I was fully against …
c) But my colleagues wanted me …
d) Of course, my plans for future wouldn’t let me …
e) But then my boss insisted on me …
f) I wasn’t too keen on …
g) But he made me …
h) And finally I came round to the idea of …
i) And I must say I don’t regret …
Ex. 16. Translate the following sentences with the emphatic construction
“It is (was) … that (who, which, when…)”.
Model. It is the method of elimination that is used for solving such equations.Именно этот метод исключения используется для решения таких уравнений.
1. It was the Arabs who preserved the Greek and Hindu scientific writings through the Dark Ages of Europe.
2. It was Italy that produced the greatest algebraists during 1200–1620 period.
3. It was the Greeks’ mathematics rigour that forced them to use line segments to express numbers as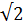 
in their geometrical algebra.
4. It was not until the next century that L. Euler supplied a proof for the case n=3.
5. It was principally through the Arabs that algebra entered Europe.
6. It was Euler who introduced the new standard notation f (x).
Ex. 17. Translate the sentences with the Infinitive Constructions into Russian.
1. We consider one of the axes of the ellipse to be the major axis, while the other – the minor axis.
2. The scientists think the orbital path of a planet around the sun to be an ellipse such that the sun is located at a focus.
3. Professor watched his student draw the number lines making the axes of a coordinate system.
4. He made us plot the ordered pairs above and connect the points with a smooth curve.
5. Let us remove the parentheses on the right side of the equation and combine similar terms.
6. I want you to make conclusion about the validity of the formula.
7. If n= - 1, then we expect the equation y = 
to describe the hyperbola.
8. One should understand all functions to be relations, but not all relations are functions.
9. Functions are considered to be parts of our everyday thinking, converting from degree Celsius to degree Fahrenheit, DNA testing, determining stock values, and the sale price of a shirt.
10. The comprehension of limits seems to create the necessity for understanding the other concepts in calculus.
11. In order to demonstrate the unity of various approaches to this concept, we are supposed to combine intuitive arguments with rigorous proofs of propositions.
12. The above definition proved to be easily translated into the rigorous mathematical language.
13. The graph of the even function is believed to be symmetric with respect to the y-axis and that of the odd function is known to be symmetric with respect to the origin.
14. The method of math induction turns out to be very helpful in proving many statements about integers.
15. A geometric progression is certain to be a sequence in which each term is determined by multiplying the preceding term by a constant.
16. When we try to prove the truth of some general statement, it’s quite natural for us to check its validity in a particular case.
17. It’s for you to decide how to determine this function: by means of tables
or graphically.
18. You must factor a polynomial expression, i.e. represent it as a product
of the irreducible polynomial for the equation to be solved.
19. It was essential for us to understand that the sign of the discriminate is
an important characteristic of the quadratic equation.
20. I asked for the function to be determined on the interval.
21. His idea is for us to understand that a coordinate system locates points in a
plane by means of numbers.
Ex. 18. Topics for discussion.
1. Dwell on the notion of a function as a correspondence.
2. Give the classification of real-valued functions.
3. Speak about the relation between the concept of a function and that of a graph.
4. Show some special properties of a function using the properties of a graph.
5. Prove or disprove the statement that equation in x and y defines y as a function of x.
Ex. 19. Read the text and answer the following questions.
1. What did a word ‘function’ mean to mathematicians a century ago?
2. When and why did sufficient grounds appear to extend the notion
of a function?
3. What is the key idea of the function definition used today?
TEXT B.
FUNCTIONS
We now turn to the discussion of the fundamental notion of a function or mapping. It will be seen that a function is a special kind of a set, although there are other visualizations which are often suggestive.
To the mathematician of a century ago the word “function” ordinarily means a definite formula, such as f(x) = x2 + 3x + 5, which associates to each real number x another real number f(x). The fact that certain formulas, such as
g(x) = √x – 5, do not give rise to real numbers for all real values of x was, of course, well-know but was not regarded as sufficient grounds to require an extension of the notion of function. Probably one could arouse controversy among those mathematicians as to whether the absolute value h (x) = │x│ of a real number is an “honest function” or not. For, after all, the definition of │x│ is given “in pieces” by
│x│ = x, if x ≥ 0, │x│ = - x, if x < 0.
As mathematics developed, it became increasingly clear that the requirement that a function be a formula was unduly restrictive and that a more general definition would be useful. It also became evident that it is important to make a clear distinction between the function itself and the values of the function.
Our first revised definition of a function would be:
A function f from a set A to a set B is a rule of correspondence that assigns to each x in a certain subset D of A, a uniquely determined element f (x) of B.
Certainly, the explicit formulas of the type mentioned above are included in this definition. The proposed definition allows the possibility that the function might not be defined for certain elements of A and also allows the consideration of functions for which the set A and B are not necessarily real numbers.
However suggestive the proposed definitions may be, it has a significant defect: it is not clear. There remains the difficulty of interpreting the phrase “rule of correspondence”. The most satisfactory solution seems to define “a function” entirely in terms of sets and the notions introduced above.
The key idea is to think of the graph of the function, that is, a collection of the ordered pairs.
Definition. Let A and B be sets. A function from A to B is a set f of ordered pairs in A x B with the property that if (a, b) and (a', b') are elements of f, then b = b'. The set of all elements of A that can occur as first members of elements in f is called the domain of f and will be denoted D (f). The set of all elements of B that can occur as second members of elements f is called the range of f (or the set of values of f) and will be denoted by R (f). In case D (f) = A, we often say that f maps A into B (or is a mapping of A into B) and write f : A → B.
If (a, b) is an element of a function f, then it is customary to write b = f (a) or f : a → b instead of (a, b) Є f. We often refer to the element b as the value of f at the point a, or the image under f of the point a.
Ex. 20. Say these sentences in English.
Основныепонятия функции.
Если каждому значению х изнекоторой области D поставлено в соответствие значение переменной у, то говорят, что в области D задана функция у аргумента х:
y = f(x)
Это типичное обозначение функции. Область D называется областью определенияфункции, а совокупность значений переменной у - областью ее изменения.Уравнение у = f(x) можно интерпретировать графически как уравнение кривой в х, у - плоскости. Говорят, что функция f задает отображение множества X на множество Y, если для любого y є Y существует такое х є Х,что f(x) = у. Это отображение является взаимно однозначным, если из равенства f(x) = f(z) следует, что
x = z.
Функции можно также задавать с помощью таблиц.
Примером такого задания является нижеприведенная таблица.
Таблица 1
| x | -3 | -2 | -1 | ||||
| f (x) | -1 |
Кроме того, зависимость между переменными х и у можно задавать графически. Каждая пара чисел в вышеприведенной таблице задает точку в плоскости х 0 у.Если нанести эти точки и соединить их плавной кривой, то мы получим график функции у = f (х).
UNIT VI
Grammar: Conditional Sentences. Mixed Conditionals. Inversion.