Numbers 4.12 and 3.5 being names for fractional numbers, we may write them as complex fractions.

b) After the experimental work had been completed, they could publish the results obtained.

The experimental work having been completed, they could publish the results obtained.

1. As the speed of light is extremely great, we cannot measure it by ordinary methods. 2. After the first question had been considered, we could pass over to the next one. 3. Since other conditions are equal, the acceleration will be the same. 4. After the set of axioms had been accepted, we could predict many new properties of the system involved. 5. After the theorem had been stated, the students could begin solving it. 6. After all the necessary changes had been made, the experiment showed different results. 7. Since a and b are real numbers, the general expression a + bi represents a complex number. 8. As the measure of the circumference is given, you can find the area of the interior of the circle.

Ex. 5. Translate the sentences into Russian paying attention to the Objective Participial Constructions and Participle II in the construction “have something done”

I saw him entering the University building.	Я видел, как он входил в здание университета.
She wants to have several copies ofthis article made.	Она хочет, чтобы ей сделали несколько копий этой статьи.

1. We saw her reading a book in the library. 2. The students had their tests checked a few days ago. 3. She heard him making a speech at the conference. 4. The teacher listened to the text being translated from Russian into English by the student. 5. The supervisor had the report presented last week. 6. We are having the results of the test announced at the moment. 7. I saw her talking to the lecturer. 8. We didn’t notice him entering the classroom. 9. I’ve never heard him speaking English. 10. Can I have my documents typed immediately?

Ex. 6. Translate the sentences into English, use the Absolute Participle Construction.

1. Так как температура постоянно изменяется, мы не можем сделать точных измерений. 2. Когда занятия окончились, студенты начали обсуждать свои планы на выходной день. 3. Если дана длина окружности, можно найти площадь внутренней части круга. 4. Существует много методик обучения иностранным языкам, причем данная методика – самая эффективная. 5. В предыдущей главе рассматривались многоугольники, этот вид геометрических фигур является очень важным в изучении геометрии. 6. Поскольку квадрат любого числа положительный, то квадратный корень от отрицательного числа является мнимым. 7. Если даны две точки А и В, мы можем начертить прямую, соединяющую их.

Pre-Reading Activity

Guess the meaning of the following words:

collection (n) [kq'lekSqn] algebra (n) ['xlGIbrq]

object (n) ['ObGIkt] phrase (n) ['freIz]

element (n) ['elImqnt] symbol (n) ['sImbql]

theory (n) ['TIqrI] standard (a) ['stxndqd]

concrete (a) ['kOnkrJt] season (n) ['sJzqn]

real (a) ['rIql] variation (n) [vFrI'eISqn]

interest (n) ['IntrIst] idea (n) [aI'dIq]

abstract (a) ['xbstrqkt] vertical (a) ['vWtIkql]

sphere (n) ['sfIq] fact (n) ['fxkt]

special (a) ['speSql] mathematics (n) [mxTI'mxtIks]

Read and learn the basic vocabulary terms.

set (n) [set] множество

belong (v) [bI'lON] принадлежать

introduce (v) [Intrq'djHs] вводить, представить

capital (a) ['kxpItql] заглавный

convention (n) [kqn'venSqn] договоренность, условие

keep (to) (v) [kJp] придерживаться, держаться (ч-л)

rigidly (adv) ['rIGIdlI] строго

occur (v) [q'kW] встречаться, происходить

currently (adv) ['kArqntlI] в настоящее время

find out (v) ['faInd'aut] узнать, выяснить

specify (v) ['spesISaI] точно определять

list (v) ['lIst] перечислять

notation (n) [nou'teISqn] обозначение, запись

enclose (v) [In'klquz] заключать

curly (a) ['kWlI] фигурный

mention (v) ['menSqn] упоминать, ссылаться

denote (v) [dI'nqut] обозначать

allow (v) [q'lau] позволять

property (n) ['prOpqtI] свойство

precisely (adv) [prI'saIslI] точно, определенно

exact (a) [Ig'zxkt] точный

infinite (a) ['InfInqt] бесконечный

finite (a) ['faInaIt] конечный

notion (n) ['nquSqn] понятие

turn out (v) [tWn'Qut] оказываться, выпускать, выводить

confuse (v) [kqn'fjHz] путать, смешивать

empty (a) ['emptI] пустой

distinguish (v) [dI'stINgwIS] различать, выделять, распознавать

establish (v) [Is'txblIS] установить

concisely (adv) [kqn'saIslI] кратко, сжато

Notes:

none at all – ни один вообще;

to tell them apart – отличить друг от друга;

instead of a list – вместо списка (перечня);

at any rate – во всяком случае, по меньшей мере.

TEXT A

SETS

A set is a collection of objects. The objects belonging to the set are the elements or members of the set. Although in introducing set theory it is helpful to work with concrete sets, whose members are real objects, the sets of interest in mathematics always have members which are abstract mathematical objects: the set of all circles in the plane, the set of points on a sphere, the set of all numbers.

As in ordinary algebra we shall use letters to represent sets and elements, small letters being used for elements and capital letters for sets. But it is impossible to keep rigidly to this convention because sets can themselves be elements of other sets. The phrase “is a member of” occurs so often that it is convenient to have a symbol, the one currently in use is 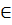. So x 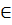S means “x is a member of S”.

A set is considered to be known if we know what its elements are – or at any rate if in theory we can find out. There are many ways of specifying a set, of which the simplest is to list all the members. The standard notation for this is to enclose the list in curly brackets. So {1, 2, 3, 4} is the set whose members are 1, 2, 3, 4 and only these, while {spring, summer, autumn, winter} is the set of seasons.

Two sets are equal if they have the same elements. We can easily write things like {1, 2, 3, 4, 4}. Despite being mentioned several times, there is only one 4 in the set, which being thus equal to {1, 2, 3, 4}. When using the curly bracket notation, elements listed more than once are thought of as occurring once in the set. The order inside the brackets makes no difference. The set {1, 2, 3, 4, 4} has the same elements as {1, 2, 3, 4}, so is the same set.

More generally, a symbol such as {all epic poems} denotes the set of all epic poems. A variation of this idea allows us to write {x|x is an epic poem} for the same set. The vertical bar may be read as “such that”, and the set of all x such that x is an epic poem is the same as the set of all epic poems. The set

{n|n is an integer and 1 ≤ n ≤ 4} is the same as the set {1, 2, 3, 4}.

Instead of a list, we give a property which specifies precisely the elements we wish to be included in the set. If we are careful with our definitions, making sure that we specify the exact property we want, this is as good as a list, and is usually more convenient. For sets with infinitely many members, such as

{all whole numbers}, it is in any case impossible to give a complete list. The same is true for sets with a sufficiently large finite set of elements.

The mathematical notion of a set allows sets with only one member or even no members at all. If you specify a set by some property it may turn out later that there is only one object with that property or none at all. Sets with one element must not be confused with the element itself. It is not true that x and {x} are equal; {x} has just one member, namely x, while x may have any number of members depending on whether or not it is a set, and if it is, which set.

For exactly the same reasons that we allow sets with just one element, we have to allow sets with no elements at all. A set with no elements is called an empty set. A fact now emerges which many people find surprising: there is only one empty set. All empty sets are equal. Any two empty sets are equal because, in the absence of any members to distinguish them by, there is no way to tell them apart. Having established that there is just one empty set we can give it a symbol, the current one being Ø (which is a special symbol). The empty set is not “nothing” …, nor does it fail to exist. It is just as much in existence as any other set. It is its members that do not exist. It must not be confused with the number 0: for 0 is a number, whereas Ø is a set. Ø is one of the most useful sets in mathematics. One of its uses is to express concisely that something does not happen.

Post-Reading Activity.

Ex. 7. Answer the following questions:

1. What is a set? 2. What are the elements of the set? 3. What sets are of interest in mathematics? 4. What do we use to represent sets and elements? 5. What set is considered to be known? 6. What is the simplest way of specifying a set? 7. What is the standard notation for a set? 8. What sets are equal? 9. How can we specify the elements of a set? 10. How many members may a set have? 11. What is an empty set? 12. How is an empty set represented? 13. Does an empty set exist at all?

Ex. 8. Match the English words and word combinations with the Russian equivalents.

1. exact property; 2. to enclose the list in curly brackets; 3. to keep rigidly to the convention; 4. set theory; 5. just one element; 6. a finite set of elements; 7. elements listed; 8. concrete sets; 9. a way of specifying a set; 10. the same elements; 11. infinitely many elements; 12. standard notation; 13. abstract objects; 14. a complete list; 15. it makes no difference; 16. the sets of interest in mathematics; 17. members of the set.

a. члены множества; b. множества, вызывающие интерес в математике; c. конкретные множества; d. абстрактные объекты; e. способ определять множество; f. обычно принятое обозначение; g. заключить перечень в фигурные скобки; h. одни и те же элементы; i. перечисленные элементы; j. точное свойство; k. бесконечное число элементов; l. полный перечень; m. конечное число элементов; n. только один элемент; o. не имеет значения; p. теория множества; q. строго придерживаться условия.

Ex. 9. Fill in the blanks with the words from the box.

empty, members, to list, notation, specifying, difference, precisely, the same

1. The objects belonging to the set are the elements or … of the set. 2. There are many ways of … a set. 3. The simplest way of specifying a set is … all the members. 4. The standard … is to enclose the list in curly brackets. 5. Two sets are equal if they have … elements. 6. The order inside the brackets makes no … 7. Instead of a list, we give a property which specifies … the elements. 8. A set with no elements is called an … set.

Ex. 10. Ask questions for which the given sentences are answers.

1. A set is a collection of objects. (What?) 2. The objects belonging to the set are the elements or members of the set. (Which?) 3. The sets of interest in mathematics always have members which are abstract mathematical objects. (What?) 4. In the algebra of sets we use letters to represent sets and elements. (Where?) 5. A set is considered to be known if we know what its elements are. (When?) 6. There are many ways of specifying a set. (How many?) 7. The standard notation is to enclose the list in curly brackets. (What?) 8. Two sets are equal if they have the same elements. (When?) 9. Instead of a list, we give a property which specifies precisely the elements of the set. (What?) 10. For sets with infinitely many members, it is impossible to give a complete list. (Which?) 11. The mathematical notion of a set allows sets with only one member or even no members at all. (What?) 12. A set with no elements is called an empty set. (What?) 13. All empty sets are equal. (What?)

Ex. 11. Find out whether the statements are true or false. Use introductory phrases.