Часть I . Определение нормальных глубин, критической глубины и критического уклона в канале

Определения и предварительные замечания

Равномернымназывается движение, при котором скорости жидкости не меняются с течением времени и по длине потока, то есть в сходственных точках поперечных сечений скорости одинаковы по всей длине потока.

Если при движении скорости жидкости, не изменяясь во времени, меняются по длине потока, то такое установившееся движение называется неравномерным. Такой характер движения бывает при сужении или расширении потока в реке, на повороте, в конфузорах и диффузорах. На практике случаи неравномерного движения воды встречаются значительно чаще, чем случаи равномерного.

Важнейшей задачей расчета неравномерного движения является построение кривых свободной поверхности потоков. При неравномерном движении глубины потока вдоль течения изменяются. Если глубина уменьшается вниз по течению, кривая свободной поверхности называется кривой спада. Если глубина потока вниз по течению увеличивается, кривая свободной поверхности называется кривой подпора.

В выполняемой работе рассматриваются случаи неравномерного движения в призматических руслах трапецеидального или прямоугольного сечений.

При этом заметим, что один и тот же расход воды в потоке Q может быть пропущен через такое русло при различном его наполнении, то есть при разных глубинах в каждом сечении. При больших глубинах вода будет двигаться с меньшей скоростью, при малых глубинах – с большей. Однако равномерное движение заданного расхода возможно только при одной глубине, определяемой формулой

.

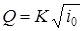(1.1)

Эта формула называется формулой Шези, она связывает расход и геометрические характеристики потока.

Здесь:

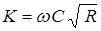– модуль расхода или расходная характеристика;

i₀– уклон дна русла;

ω – площадь живого сечения потока;

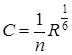– коэффициент Шези;

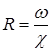– гидравлический радиус живого сечения;

n – коэффициент шероховатости поверхности дна и откосов русла;

χ – смоченный периметр живого сечения.

В формуле Шези глубина потока в неявном виде входит в модуль расхода, каждому значению K соответствует определенное значение глубины потока.

Глубина равномерного движения потока жидкости h₀ называется нормальной глубиной для данного расхода. Отвечающее нормальной глубине значение расходной характеристики K₀ будем называть нормальной расходной характеристикой. В заданном русле при всех глубинах, отличных от нормальной, заданный расход будет проходить при неравномерном режиме движения. Каждому расходу в определенном русле соответствует свое значение нормальной глубины.

Удельной энергией сечения потока называют удельную энергию, рассчитанную относительно плоскости сравнения, проведенной через низшую точку живого сечения потока – плоскость O–O на рис. 1.1.

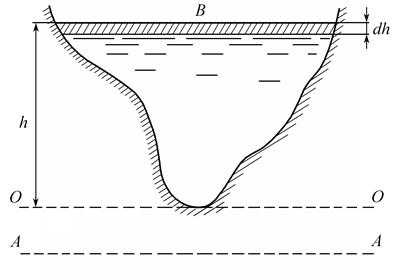
Рис. 1.1

Обозначив удельную энергию сечения через Э, запишем соответствующий трехчлен Бернулли:

.

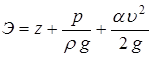Нетрудно убедиться, что в открытых руслах для любой точки в потоке

,

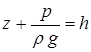то есть величина удельной потенциальной энергии равна глубине воды в сечении.

Тогда

.

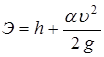(1.2)

Таким образом, удельная энергия сечения складывается из удельной потенциальной энергии h и удельной кинетической энергии 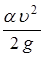. С учетом выражения средней скорости движения через расход ,

.

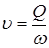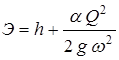(1.3)

Из уравнения (1.3) видно, что даже при постоянном расходе Q удельная энергия сечения при неравномерном движении меняется с изменением глубины потока h и, соответственно, площади живого сечения ω. Характер зависимости, определяемый уравнением (1.2), приведен на рис. 1.2.

Рис. 1.2

На графике изменение удельной потенциальной энергии h изображено пунктирной прямой, проходящей под углом 45º к осям координат. При 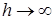удельная энергия сечения Э также стремится к бесконечности. Изменение кинетической энергии показано пунктирной гиперболой. При увеличении глубины возрастает площадь живого сечения потока, скорость, а с ней и кинетическая энергия уменьшаются. При 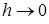площадь живого сечения стремится к нулю ( 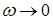), скорость и кинетическая энергия возрастают. Суммарная кривая, отображающая изменение полной удельной энергии сечения состоит из двух ветвей. Вдоль верхней ветви энергия Э возрастает с увеличением глубины h, это увеличение происходит за счет увеличения потенциальной энергии. Вдоль нижней ветви энергия Э возрастает с уменьшением глубины за счет увеличения кинетической энергии. Очевидно, что функция Э имеет минимум в точке соединения двух своих ветвей.

Глубина, при которой удельная энергия сечения достигает минимального значения Э_min, называется критической глубиной h_кр. Для определения критической глубины можно воспользоваться условием минимума удельной энергии сечения Э – функции, определяемой формулой (1.3). Возьмем производную этой функции по h:

.

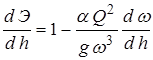Приращение площади живого сечения при изменении глубины может быть представлено (рис. 1.1) как 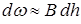, где B – ширина живого сечения по верху. Тогда

.

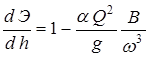При глубине, равной критической 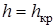, функция Э имеет минимум, значит, в этой точке производная 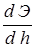должна быть равна нулю, тогда

.

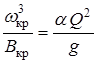(1.4)

Здесь 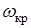и 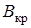– площадь живого сечения и ширина его по верху при критической глубине h_кр.

Формула (1.4) позволяет определить критическую глубину для русел любой формы.

Из формулы (1.4), определяющей величину критической глубины, можно видеть, что эта глубина зависит от формы и размеров русла и от расхода, но не зависит от уклона и шероховатости стенок русла. В то же время при равномерном движении нормальная глубина, определяемая формулой (1.1), зависит как от расхода, формы и размеров русла, так и от его уклона и шероховатости. При изменении уклона критическая глубина не меняется, а нормальная – меняется. В зависимости от уклона нормальная глубина может быть больше или меньше критической, а при некотором уклоне нормальная глубина может стать равной критической. Уклон дна, при котором нормальная глубина становится равной критической, то есть 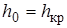, называется критическим уклоном. При критическом уклоне расход определится по формуле для равномерного движения

.

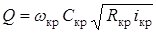Подставив это выражение в формулу (1.4) и решив его относительно 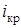, получим

.

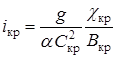(1.5)

При уклоне дна меньше критического, 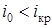, нормальная глубина больше критической – 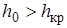. Такие уклоны называют пологими. При уклоне дна больше критического, 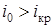, нормальная глубина меньше критической – 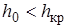. Такие уклоны называют крутыми.

В зависимости от соотношения действительной и критической глубин потока различают три состояния потока.

Если действительная глубина больше критической, состояние потока называют спокойным. Основным видом энергии такого потока является потенциальная энергия.

В тех сечениях, где глубина потока равна критической, состояние потока называют критическим.

При глубине меньше критической поток называют бурным. Энергия потока сосредоточена главным образом в кинетической энергии.

В курсе общей гидравлики для расчета кривых свободной поверхности неравномерного потока в цилиндрических или призматических руслах была получена формула

.

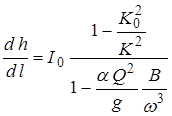(1.6)

Это – формула зависимости глубины потока от расстояния вдоль потока, то есть она описывает форму свободной поверхности. Анализ этой зависимости позволил определить следующие закономерности.

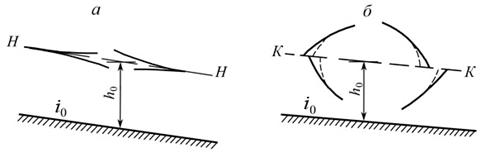
Рис. 1.3

При неравномерном движении воды кривые свободной поверхности могут приближаться к линиям нормальной (при i₀ > 0) или критической глубины, которые для цилиндрических и призматических русел остаются постоянными на всем их протяжении. При этом к линии нормальных глубин кривая свободной поверхности приближается асимптотически (рис. 1.3.а), а к линии критических глубин стремится подойти перпендикулярно (под крутым углом) (рис. 1.3.б).

Формы кривых свободной поверхности потока зависят от уклона дна русла, а также от действительной глубины потока h на входе в рассматриваемый участок и соотношения этой глубины с нормальной и критической глубинами. При этом возникают следующие варианты кривых свободной поверхности.