Имени адмирала С.О. Макарова»

Имени адмирала С.О. Макарова»

Кафедра Гидротехнических сооружений, конструкций и гидравлики

ГИДРАВЛИКА

Гидротехнических сооружений

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ ВОДЫ В КАНАЛАХ

Пояснения к выполнению расчетно-графического задания

Санкт-Петербург

2017 год

УДК 627.059.01

ББК

Рецензент:

Заведующий кафедрой портов, строительного производства, оснований и фундаментов Государственного университета морского и речного флота

имени адмирала С.О. Макарова

канд. техн. наук, доц. В. Н. Смирнов

Моргунов, К. П. Гидравлический расчет неравномерного движения воды в каналах:пояснения к выполнению расчетно-графического задания /К. П. Моргунов –– СПб.: Изд-во ГУМРФ им. адмирала С.О. Макарова, 2017. – с.

Приведены пояснения к выполнению расчетно-графической работы по расчету вида и формы кривых свободных поверхностей потока при неравномерном движении в каналах трапецеидального и прямоугольного поперечного сечения.

Предназначено для бакалавров и студентов, обучающихся по направлениям 08.03.01 – Строительство (профиль – Гидротехническое строительство) и 20.03.02 – Природообустройство и водопользование (профиль – Комплексное использование и охрана водных ресурсов).

© ФГБОУ ВО «ГУМРФ имени адмирала С.О. Макарова», 2017

© К. П. Моргунов 2017

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ НЕРАВНОМЕРНОГО ДВИЖЕНИЯ ВОДЫ В КАНАЛАХ

Работа заключается в определении характеристик неравномерного движения потока воды в открытом русле.

Для выполнения работы студент получает вариант задания, в котором определены:

1. Форма поперечного сечения русла канала (трапецеидальная или прямоугольная) с некоторыми характеристиками сечения – шириной по дну b, коэффициентом заложения откоса m.

2. Количество участков рассматриваемого русла с различным уклоном дна (как правило, четыре участка), при этом задаются длины и уклоны дна этих участков.

3. Характер облицовки (покрытия дна и откосов).

4. Расход воды в потоке Q.

5. Некоторые характерные глубины.

6. Для канала прямоугольного сечения при истечении потока из-под щита задается высота поднятия щита h_щ и коэффициент сжатия струи ε.

Далее процесс выполнения работы разбивается на три части.

В первой части «Определение нормальных глубин, критической глубины и критического уклона в канале» находятся основные параметры неравномерного потока, проводится качественный анализ и определение вида кривых свободной поверхности, анализируются возможные формы их сопряжений для всех участков проектируемого канала.

Во второй части «Численный расчет кривых свободной поверхности по участкам канала» выполняется программирование и расчет на ПК кривых свободной поверхности. Одна или две кривых по согласованию с преподавателем рассчитываются вручную.

В третьей части «Расчет гидравлического прыжка. Построение кривой свободной поверхности по трассе канала» уточняется форма сопряжения с кривыми свободной поверхности соседних участков, определяется местоположение гидравлического прыжка и потери энергии в нем. В заключение выполняется построение кривой свободной поверхности для всей трассы канала.

Уклон дна равен нулю

В горизонтальном канале (при ) не может быть равномерного движения и, следовательно, не может быть нормальной глубины. Условно принимаем значение нормальной глубины равным бесконечности. Неравномерное движение происходит в двух зонах – b и c (рис. 1.7).

Рис. 1.7

Обратный уклон дна

В случае если русло имеет обратный уклон, , то, как и в случае нулевого уклона дна, при движении потока не может быть нормальной глубины и неравномерное движение будет в двух зонах – b и c (рис. 1.8).

Рис. 1.8

Выполнение расчетов

В соответствии с заданием на работу, рассматриваемый канал состоит из четырех участков с различными длинами и уклонами. При этом расход вдоль канала остается постоянным и одинаковым для каждого участка. Поперечное сечение канала на всех участках также одинаково.

Напомним, что нормальная глубина (то есть, глубина равномерного течения) зависит от расхода, формы и размеров русла, а также от его уклона и шероховатости. Значит, для каждого участка канала будет своя нормальная глубина.

Критическая глубина зависит от формы и размеров русла и от расхода, но не зависит от уклона и шероховатости стенок русла. Поэтому, на всех участках канала критическая глубина будет одинакова.

1.1. Определение нормальных глубин для участков канала.

Сначала из формулы (1.1) определяется модуль расхода, соответствующий заданному расходу и уклону дна первого участка канала

.

Затем для первого участка строится теоретический график зависимости модуля расхода от глубины потока . Подготовку к построению графика удобно провести в табличной форме. Задаваясь несколькими (пятью – шестью) произвольными значениями глубины потока h, последовательно вычисляют ω, χ, R, С и, наконец, K.

Значения этих величин зависят от формы и размеров канала.

Для канала трапецеидальной формы смоченный периметр и площадь живого сечения определяются по формулам (рис. 1.9):

; ;

где b – ширина канала по основанию (по дну), m – коэффициент заложения откоса, h – глубина воды на участке канала.

Рис. 1.9

Для канала прямоугольной формы коэффициент заложения откоса равен нулю и смоченный периметр и площадь живого сечения определятся как:

; .

Затем рассчитываются гидравлический радиус R, коэффициент Шези C и модуль расхода K:

; ; .

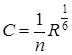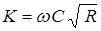При расчете коэффициента Шези C используется коэффициент шероховатости n, значение которого определяется характером облицовки дна и откосов русла. Характер облицовки приведен в задании на выполнение работы, соответствующий этой облицовке коэффициент шероховатости определяется из гидравлических справочников. Ввиду значительного разброса справочных значений, рекомендуется принимать следующие коэффициенты шероховатости (таб. 1.1).

Таблица 1.1

Характер облицовки	Бетон	Земля	Булыжное мощение
Коэффициент шероховатости n	0,020	0,025	0,030

Полученные значения K обязательно должны быть как больше, так и меньше ранее найденного значения K_зад. Если значения K оказываются существенно отличными от K_зад, следует изменить выбранные ранее значения глубин h таким образом, чтобы соответствующие им K не отличались от K_задболее, чем на ± (30 ÷ 50) %. Полученные значения заносятся в таблицу.

Таблица 1.2

Участок № … (K_зад = …)

№ п/п	h, м	χ, м	ω, м2	R, м		С	K

По данным таблицы 1.2 строится график зависимости для первого участка (рис. 1.10). По этому графику, зная величину K_зад, определяют нормальную глубину h₀ на первом участке.

Рис. 1.10

Аналогичные вычисления по определению нормальных глубин проводятся и для других участков канала, уклоны дна которых не равны нулю. При уклоне дна, равном нулю, как уже отмечалось, равномерное движение потока невозможно, поэтому принимается h₀ = ∞.

На участках с отрицательным уклоном дна для последующих расчетов необходимо по той же методике найти так называемую «фиктивную» нормальную глубину потока , то есть глубину потока, который двигался бы по данному участку канала с тем же расходом, но в обратную сторону по уклону дна

.

Тогда для участка с отрицательным уклоном дна

.

1.2. Определение критической глубины потока.

Для нахождения критической глубины h_кр в руслах трапецеидального сечения также используется графоаналитический способ. В этом случае справедливо уравнение (1.4)

.

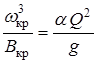Здесь B – ширина потока поверху (по зеркалу) (рис. 1.1).

Для русел трапецеидального сечения .

Строится график зависимости (рис. 1.11). Для этого также удобно использовать таблицу.

Таблица 1.3

№ п/п	h, м	ω, м2	ω3	B, м

Аналогично предыдущему, при вычислениях берется пять – шесть произвольных значений глубин h, при которых полученные величины будут в пределах ± (30…50) % от , а точки на графике должны находиться по обе стороны от значения .

Учитывая, что при h = h_кр соблюдается равенство и, принимая для турбулентного режима течения α ≈ 1,0, по заданному расходу вычисляем величину , а затем по графику рис. 1.11 определяем значение критической глубины h_кр.

Рис. 1.11

Для русел прямоугольного сечения существует аналитическая зависимость для вычисления критической глубины:

,

где – удельный расход.

Для прямоугольного сечения B = b.

1.3. Определение критического уклона.

Критическим уклоном дна будет такой уклон, при котором нормальная глубина становится равной критической, то есть 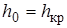. Величина критического уклона определяется формулой (1.5)

,

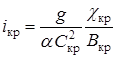где , , – соответственно, значения смоченного периметра, коэффициента Шези и ширины по зеркалу при глубине в канале h_кр.

Критический уклон можно также определить и графоаналитическим способом, используя имеющийся график . Для этого, задаваясь несколькими (как обычно, пятью – шестью) значениями уклона дна i₀ и зная расход воды в канале Q, вычисляют соответствующие этим уклонам значения . Затем по графику (рис. 1.10) определяют соответствующие рассчитанным K_задзначения нормальной глубины h₀ и строят график (рис. 1.12).

Таблица 1.4

№ п/п	i0	, м3/с	h0, м

Рис. 1.12

На этот же график наносится значение критической глубины h_кр. В отличие от нормальной глубины, критическая глубина для заданного поперечного сечения потока зависит только от расхода Q. Поэтому на графике рис. 1.12 функция отразится в виде горизонтальной прямой. Точка пересечения кривой и прямой соответствует значению критического уклона i_кр.

1.4. Определение вида свободных поверхностей.

В этом разделе необходимо определить характер кривых свободной поверхности потока на рассматриваемых участках русла. Делается это следующим образом.

Уклоны участков определены заданием на выполнение работы. Заданные уклоны по участкам нужно сравнить с рассчитанными критическими уклонами на участках.

Схематично рисуем условный профиль канала (рис. 1.13), для удобства дальнейших построений на границах участков проводим вспомогательные вертикали. На этот профиль наносим рассчитанные критическую (одну по всем участкам) и нормальные (для каждого участка) глубины.

Рис. 1.13

На четвертом участке (в соответствии с заданием) уклон равен нулю или отрицателен. Поэтому на нем невозможно равномерное движение потока и, следовательно, нет нормальной глубины (принято считать её бесконечной).

Затем проводим принципиальный анализ формы кривых свободной поверхности по участкам. Для такого анализа нужно оттолкнуться от некоторых уже известных глубин потока на участках.

В задании на выполнение работы исходные глубины определены следующим образом:

· для канала трапецеидального поперечного сечения определены глубина в начале первого участка (h_нач = 0,95h_кр) и глубина в конце последнего 4-го участка (h_кон = 1,05h_кр);

· для канала прямоугольного поперечного сечения определено, что вода в канал поступает из-под щита, задана высота поднятия щита h_щ и коэффициент сжатия струи ε; тогда можно определить глубину в начале первого участка h_нач = ε h_щ; глубина в конце последнего 4-го участка задана (h_кон = 1,05h_кр).

Кроме того, при расчете кривых свободной поверхности необходимо руководствоваться следующим правилом: в конце участка русла, имеющего уклон меньше критического (то есть там, где русло обрывается и поток переходит в свободно ниспадающую струю, либо в точке перелома дна, где уклон переходит в уклон ), устанавливается критическая глубина h = h_кр.

Помимо этого нужно понимать, что при движении по участкам большой длины – 200 – 300 м (какими и являются участки в выполняемом задании), поток всегда стремится к равномерному характеру движения, при котором глубина его приближается к нормальной.

Исходя из этого, начинаем строить кривые свободной поверхности.

Пусть на первом участке заданный уклон окажется больше критического (индекс «1» означает первый участок). Либо оказалось, что критическая глубина больше нормальной . Это значит, что в соответствии с рис. 1.5, в зависимости от действительной глубины потока в начале участка h_нач, на первом участке могут возникнуть три зоны течения. Поскольку глубина в начале участка меньше критической (h_нач = 0,95h_кр), но больше нормальной , то кривая свободной поверхности будет иметь вид кривой спада типа b₂, асимптотически стремясь к нормальной глубине (рис. 1.14).

Рис. 1.14

Если заданный уклон на первом участке меньше критического, либо нормальная глубина больше критической, реализуется картина течения, представленная на рис. 1.4. В этом случае, с учетом того, что начальная глубина меньше критической, свободная поверхность потока будет иметь вид кривой подпора типа c₁, под крутым углом приближаясь к критической глубине.

Следующая по ходу течения глубина, известная нам, – это глубина на границе второго и третьего участка. В соответствии с изложенным выше правилом, на изломе от глубины меньше критической к глубине больше критической устанавливается глубина равная критической, h = h_кр. От этой вертикали будем строить кривые свободной поверхности на втором участке (вверх по течению) и на третьем участке (вниз по течению). При этом руководствуемся тем, что поток всегда стремится к равномерному характеру движения, при котором глубина его приближается к нормальной.

Тогда кривая свободной поверхности на втором участке от границы между вторым и третьим участками двигаясь вверх по течению и стремясь приблизиться к нормальной, будет иметь вид кривой спада b₁ (рис. 1.15).

Рис. 1.15

На третьем участке кривая, двигаясь вниз по течению от критической глубины к нормальной, будет иметь вид кривой спада b₂ (рис. 1.16).

Рис. 1.16

Уклон четвертого участка (в соответствии с заданием) равен нулю или отрицателен, глубина в конце участка h_кон = 1,05h_кр. Тогда в соответствии с рис. 1.8 или 1.9 на четвертом участке установится кривая спада типа b₄ или b₅ (рис. 1.17).

Рис. 1.17

Проведя такого рода качественные рассуждения и построения, обнаруживаем, что на границах первого и второго, а также третьего и четвертого участков возникают разрывы кривых свободной поверхности. При этом глубине потока необходимо преодолеть критическую глубину. Как известно, переход от течения с глубиной меньше критической (бурного состояния потока) к течению с глубиной больше критической (спокойное состояние потока) происходит посредством гидравлического прыжка. Следовательно, сопряжение кривых свободной поверхности на этих участках будет осуществляться путем гидравлического прыжка. Местоположение и характеристики гидравлического прыжка будут определены в последующих частях работы.

Изложенная методика качественного анализа кривых свободной поверхности потока справедлива как для трапецеидального, так и для прямоугольного поперечного сечения русла канала.

ЛИТЕРАТУРА

1. Моргунов К. П. Гидравлика: учебник. СПб.: Издательство «Лань», 2014. – 288 с.

2. Ивановский Ю. К., Рябов Г. Г., Ушакевич А. Н. Гидравлический расчет неравномерного движения воды в каналах: учебно-методическое пособие по выполнению курсовой работы. – СПб.: СПГУВК, 2010 – 34 с..

2. Чугаев P.Р. Гидравлика. — М. Л.: ГЭИ, 1971.

3. Павловский Н.Н. Краткий гидравлический справочник. — М.: Стройиздат, 1940.

Приложение. Функции Бахметьева

О Г Л А В Л Е Н И Е

ВВЕДЕНИЕ. Гидравлический расчет неравномерного движения воды в каналах . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Часть I. Определение нормальных глубин, критической глубины и критического уклона в канале . . . . . . . . . . . . . . . . . . . . . .
	Определения и предварительные замечания . . . . . . . . . . .
	Выполнение расчетов . . . . . . . . . . . . . . . . . . . . . . . .
		1.1. Определение нормальных глубин для участков канала .
		1.2. Определение критической глубины потока . . . . . . .
		1.3. Определение критического уклона . . . . . . . . . . . .
		1.4. Определение вида свободных поверхностей . . . . . .
Часть II. Расчет кривых свободной поверхности по участкам канала
		2.1. Расчет на персональном компьютере . . . . . . . . . .
		2.2. Расчет ручным способом . . . . . . . . . . . . . . . . .
Часть III. Расчет гидравлического прыжка. Построение кривой свободной поверхности по трассе канала . . . . . . . . . . . . . . .
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Приложение. Функции Бахметьева . . . . . . . . . . . . . . . . . . .

имени адмирала С.О. Макарова»