Понятия о линейных и угловых перемещениях

При изгибе

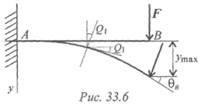
Под действием поперечных нагрузок продольная ось искривля­ется (рис. 33.6). Если материал подчиняется закону Гука, после сня­тия нагрузок брус выпрямляется, поэтому изогнутую ось бруса на­зывают упругой линией. По форме упругой линии балки можно су­дить о перемещениях при изгибе.

При прямом поперечном изгибе бруса его ось, искривляясь, остается

Тема 2.6. Понятие о касательных напряжениях при изгибе 273

в силовой плоскости. В результате деформации бруса каждое из его поперечных сечений получает вертикальное и горизонтальное перемещение, а само сечение поворачивается на некоторый угол θ.

Деформации должны иметь упру­гий характер, они достаточно малы. В этом случае горизонтальные пе­ремещения сечений ничтожно малы и не учитываются. Рассматривают вертикальные перемещения центра тяжести сечения, называемые про­гибами (у). Максимальные прогибы обозначают f = у_max. Для обеспече­ния нормальной работы устанавливаемого на балках оборудования проводят расчет на жесткость.

Условие жесткости выражается неравенством

f ≤ [ f ],

где f — максимальный расчетный прогиб балки; [f] — допускаемый прогиб.

Иногда проверяется угол поворота сечения θ < [θ].

Допускаемый прогиб невелик: от 1/200 до 1/1000 пролета балки; допускаемый угол поворота 1·10^-3 рад.

Существует несколько методов определения перемещений сече­ний при изгибе. Один из них основан на дифференцировании урав­нения упругой линии, более рациональный способ — использование интегралов Мора. Метод Мора — универсальный способ определе­ния линейных и угловых перемещений в любых системах.

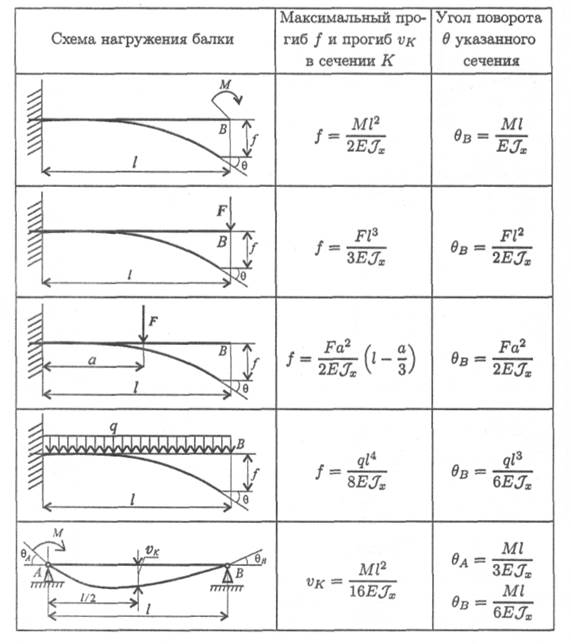
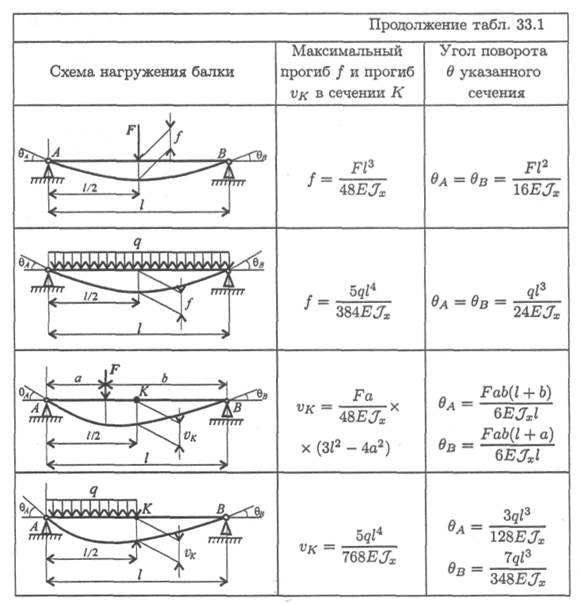
Для облегчения расчетов на жесткость можно использовать формулы прогибов и углов поворота сечений балок для простейших случаев нагружений. Наиболее распространенные случаи нагружения и расчетные формулы приведены в таблице.

При решении используем принцип независимости действия сил. Заданный случай нагружения делится на составляющие, для кото­рых прогибы рассчитываются по известным табличным формулам, результаты расчетов суммируются.

Ограничение угла поворота вводится для обеспечения нормаль­ной работы подшипников скольжения и роликовых подшипников.

В этом случае проверяется дополнительное условие жесткости:

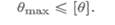
274 Лекция 33

Формулы для определения прогибов и углов поворота сечений балок

Таблица 33.1

Тема 2.6. Понятие о касательных напряжениях при изгибе 275

Примеры решения задач

Проверить жесткость двутавровой балки ( рис. 33.7 ). Принять

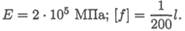Сечение балки — двутавр № 45.

Решение

Используем принцип независимости действия сил. По приведенным в

276 Лекция 33

таблице формулам рассчитываем прогиб балки в точке от каждого вида нагружения отдельно (рис. 33.7 (1, 2, 3)).

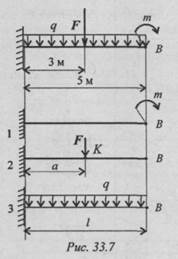Поскольку все действующие на­грузки прогибают балку вниз, результаты действия нагрузок можно сло­жить. Полученный суммарный прогиб сравним с допускаемым прогибом.

Допускаемый прогиб [f] = ——— = 25 мм.

Суммарный прогиб

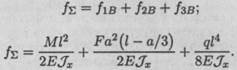
Исходные данные: т = 12 кН • м = 12 • 10⁶ Н • м; а= 3 м = 3 • 10³ мм;

F = 40kH = 40·10³H; q = 4 кН/ м = 4 Н/мм; l = 5 м = 5 • 10³ мм.

Для двутавра № 45 ГОСТ 8239-89

Тогда

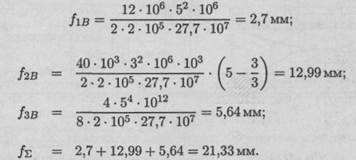
21,33 < 25 — условие жесткости выполняется. Максимальный прогиб не превышает допускаемого значения.

Тема 2.6. Понятие о касательных напряжениях при изгибе 277

Контрольные вопросы и задания

1.Какие внутренние силовые факторы возникают в сечении балки при чистом и поперечном изгибах?

2. Почему при поперечном изгибе в продольных сечениях балки
возникают касательные напряжения?

3. Каким опытом можно подтвердить возникновение касательных напряжений в продольных сечениях балки?

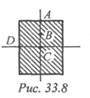
4. В какой точке поперечного сечения (рис. 33.8) касательные
напряжения при поперечном изгибе максимальны?

Варианты ответов:

1. А. 2. В. 3. С. 4. D.

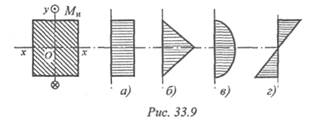
5. Выберите верную эпюру распределения нормальных напряжений при изгибе (рис. 33.9). Напишите формулу для расчета нормальных напряжений при изгибе. Изгибающий момент действует в вертикальной плоскости.

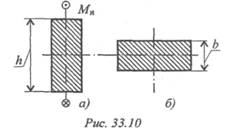
6. Как изменится максимальное нормальное напряжение в сечении (рис. 33.10а), если балку прямоугольного сечения положить плашмя (рис. 33.10б)? b= 20 мм; h = 100 мм.

7. Во сколько раз увели­чится прогиб балки, если рас­пределенную по всей длине на­грузку заменить сосредоточен­ной, приложенной в середине пролета? Использовать форму­лы для определения прогибов, приведенные в таблице 33.1.

278 Лекция 34

ЛЕКЦИЯ 34