Математические модели объектов и сау

Линейные дифференциальные уравненияописывают процессы, происходящие в каждом звене САУ в видезависимости выходной величины y(t)от входного воздействия x(t). Эти уравнения называются математическими моделями звеньев и для звеньев разной физической природы составляются по законам соответствующей науки (механики, электротехники, термодинамики и др.), нелинейные уравнения линеаризуются. Совокупность уравнений (математических моделей) взаимосвязанных звеньев САУ образуют систему дифференциальных уравнений САУ, называемую математической моделью САУ.

Для описания математической модели САУ обычно используют три способа:

1) поэлементное описание САУ с учётом взаимодействия каждого звена с другими звеньями и с внешней средой, при этом модель САУ описывается системой дифференциальных уравнений, учитывающих все параметры звеньев, входные и выходные величины (координаты) процессов управления, что обеспечивает возможность физической интерпретации всех процессов управления;

2) системное описание САУ представляется одним уравнением, которое получается из поэлементного описания САУ методом подстановок для исключения промежуточных координат процесса управления и учитывает только зависимость выходного процесса (выходной величины) САУ от входного процесса (входных величин) при утрате возможностей физической интерпретации процессов управления, происходящих внутри САУ;

3) векторно-матричное описание САУ в пространстве переменных состояния системы, позволяющее учитывать все параметры и переменные величины (координаты) САУ и вести расчёты с применением ЭВМ при возможности физической интерпретации происходящих процессов управления в САУ.

ОСНОВНЫЕ ПОНЯТИЯ О ТИПОВЫХ ЗВЕНЬЯХ

Функциональные элементы, используемые в автоматических системах, как показано в разделе 2.3, могут иметь самые различные конструктивные исполнения и принципы действия. Однако общность математических выражений, связывающих входные и выходные величины функциональных элементов, позволяет выделить ограниченное число так называемых типовых алгоритмических звеньев. Каждому типовому алгоритмическому звену соответствует определенное математическое соотношение между входной и выходной величиной. Если это соотношение является элементарным, то и звено называется элементарным.

Алгоритмические звенья, которые описываются обыкновенными дифференциальными уравнениями первого и второго порядка, получили название типовых динамических звеньев.

Типовые динамические звенья являются основными составными частями алгоритмических структур систем управления (см.раздел 2.5), поэтому знание их характеристик существенно облегчает анализ таких систем, путем построения и исследования их матмоделей.

Необходимо также понимать, что типовые динамические звенья – это упрощенно набор простейших элементов схем, выполняющих определенные функции и описываемых определенными дифуравнениями.

Типовые динамические звенья делятся на четыре группы по виду зависимости выходной величины y(t) от входного воздействия x(t) в установившихся режимах работы:

1) позиционные — выходная величина пропорциональна входному воздействию y = Kx (безынерционное, апериодическое 1-го порядка, апериодическое 2-го порядка, колебательное);

2) интегрирующие — выходная величина пропорциональна интегралу от входного воздействия y = K∫xdt (идеальное интегрирующее, реальное интегрирующее (с замедлением), изодромное);

3) дифференцирующие — выходная величина пропорциональна первой производной по времени от входного воздействия y = K dx/dt (идеальное дифференцирующее, реальное дифференцирующее (с замедлением), форсирующее);

4) запаздывающие — выходная величина равна входой величине, сдвинутой в текущем времени на время запаздывания τy = x (t –τ).

Дадим краткое описание основных динамических звеньев.

Безынерционное звено.

Безынерционное звено является простейшим среди всех типовых звеньев. Оно передает сигнал со входа на выход мгновенно, без искажений его формы. В звене может происходить только усиление или ослабление мгновенных значений входной величины.

Связь между мгновенными значениями входной величины x(t) и выходной величины y(t) описывается алгебраическим уравнением

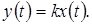
Передаточные свойства звена определяются лишь одним параметром – передаточным коэффициентом k.

На алгоритмических схемах безынерционное звено изображают в виде прямоугольника, внутри которого указывают буквенное обозначение или числовое значение передаточного коэффициента k (см. рис.).

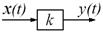
Примерами могут также служить любая электрическая цепь, состоящая из сопротивлений и являющаяся усилительным звеном; рычаги и зубчатые передачи.

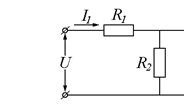
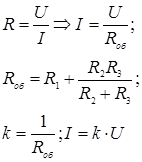
Здесь U - входная характеристика;

I - выходная характеристика.

В практике безынерционные (усилительные) звенья встречаются очень редко.

Апериодическое звено.

Динамика процесса звена описывается следующим уравнением:

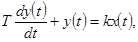
где k- передаточный коэффициент или коэффициент усиления, Т-постоянная времени, характеризующая инерционность звена.

Гармонические сигналы малой частоты (w <w_с) пропускаются звеном хорошо – с отношением амплитуд выходной и входной величин, близким к передаточному коэффициенту k. Сигналы большой частоты (w >w_с) плохо пропускаются звеном: отношение амплитуд существенно зависит от коэффициента k. Чем больше постоянная времени Т, т.е. чем больше инерционность звена, тем меньше АЧХ вытянута вдоль оси частот, или, тем уже полоса пропускания частот.

Т.о. инерционное звено первого порядка по своим частотным свойствам является фильтром низкой частоты.

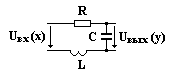
Апериодическими звеньями являются RC и RL цепи, входные и выходные величины которых связаны соответствующей передаточной функцией.

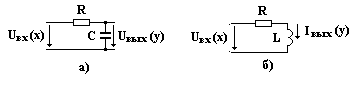
Колебательное звено.

Динамика процессов в колебательном звене описывается уравнением:

,

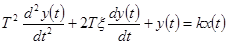где k- коэффициент усиления звена; Т- постоянная времени колебательного звена; 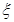- коэффициент демпфирования звена (или коэффициент затухания).

В зависимости от величины коэффициента демпфирования различают четыре типа звеньев:

а) колебательное 0< 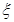<1;

б) апериодическое звено II порядка 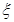>1;

в) консервативное звено 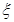=0;

г) неустойчивое колебательное звено 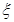<0.

Примером колебательного звена является любая RLC- цепь: