Логарифмические амплитудно-фазо-частотные характеристики сау

В расчетах и анализе САУ широкое применение находят частотные характеристики в логарифмических масштабах. Применение логарифмического масштаба позволяет наглядно изображать характеристики в большом диапазоне частот, представлять характеристики отрезками ломанных линий и определять характеристики сложных систем простым суммированием характеристик, входящих в эти системы элементов.

Логарифмические характеристики имеют меньшую кривизну и поэтому могут быть приближенно заменены ломаными линиями, составленными из нескольких прямолинейных отрезков. Причем, эти отрезки в большинстве случаев удается построить без громоздких вычислений при помощи некоторых простых правил. Кроме того, в логарифмической системе координат легко находить характеристики различных соединений элементов, так как умножению и делению обычных характеристик соответствует сложение и вычитание ординат логарифмических характеристик.

Логарифмические амплитудная (ЛАЧХ) и фазовая (ЛФЧХ) частотные характеристики, получаются путем логарифмирования передаточной функции:

lg[W(jw)] = lg[A(w) exp(jj(w)] = lg[A(w)]+lg[exp(jj(w)] = L(w) + j(w).

ЛАЧХ получают из первого слагаемого, которое умножается на 20:

L(w)=20 lg A(w). (2.18)

Логарифмическая амплитудная частотная характеристика (ЛАЧХ) звена или САУ строится в прямоугольной системе координат, где по оси ординат в линейном масштабе указывается величина ЛАЧХ в децибелах, а по оси абсцисс в логарифмическом масштабе указывается частота w в 1/с (при этом равномерные изменения частоты в 10 раз представляются декадами). Декада [дек] – любой отрезок, на котором значение частоты 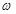увеличивается в десять раз. Децибел равен 1/10 бела. Бел равен десятичному логарифму отношения мощностей на выходе и входе звена или пропорциональному мощностям отношению квадратов напряжений, токов, скоростей или других физических величин (1 бел = lgP₂/P₁ = lgU₂₂/U₁₂). Поэтому в (2.18) множитель 20 = 2∙10, где 2 отражает логарифмирование квадрата отношения выходной и входной величин, а 10 — перевод белов в децибелы.

Ось абсцисс должна проходить через точку 0 дБ, что соответствует модулю A(w)=1, т.к. логарифм единицы равен нулю.

Ось ординат может пересекать ось абсцисс в произвольном месте, но обычно её проводят так, чтобы справа можно было разместить всю ЛАЧХ.

Логарифмическая фазовая частотная характеристика (ЛФЧХ) j(w)= arctg[V(w)/U(w)] звена или САУ строится по оси ординат в линейном масштабе, где указывается угол фазового сдвига j(w)в радианах или градусах, а по оси абсцисс указывается частота w в логарифмическом масштабе в 1/с, как в ЛАЧХ. Для элементарных звеньев она не выходит за пределы: -p ≤ j ≤ p. При построении фазовой частотной характеристики логарифмический масштаб применяют только для оси абсцисс. ЛФЧХ, отличается от ФЧХ только масштабом по оси w.

Примеры ЛАЧХ и ЛФЧХ показаны на рис. 2.13.

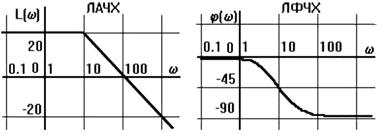
Рис. 2.13

На рис.2.14 показана ЛАЧХ L(w) (толстая линия) и соответствующая ей приближенная (асимптотическая) характеристика L_а(w) в виде прямолинейных отрезков (тонкая линия). Частоты, соответствующие точкам стыковки отрезков, называют сопрягающими и обозначают w_с. Максимальное отличие реальных ЛАЧХ от асимптотических обычно не превышает 3дБ при w =w_с.

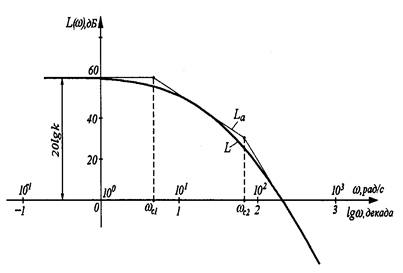
Рис.2.14

Частота, на которой L(w) = 0, т.е. A(w) = 1, называется частотой среза w_ср. Она соответствует точке пересечения ЛАЧХ с осью абсцисс. Верхняя полуплоскость ЛАХ соответствует значениям А>1 (усиление амплитуды), а нижняя полуплоскость - значениям А<1 (ослабление амплитуды).

Во многих случаях логарифмические амплитудные частотные характеристики можно построить практически без вычислительной работы. Если частотную передаточную функцию САУ представить в виде произведения сомножителей ПФ её элементов, то результирующую ЛАЧХ можно отобразить в виде асимптотической характеристики, представляющей ломаную линию, состоящую из отрезков прямых линий с наклонами, кратными величине 20дБ/дек. Физический смысл наклона – 20 дБ/дек: при увеличении частоты в 10 раз амплитуда выходного сигнала уменьшается в 10 раз, соответственно наклон – 40 дБ/дек – означает уменьшение амплитуды в 100 раз.

Для иллюстрации рассмотрим четыре типовые АЧХ и построим соответствующие им ЛАЧХ систем (рис. 2.15).

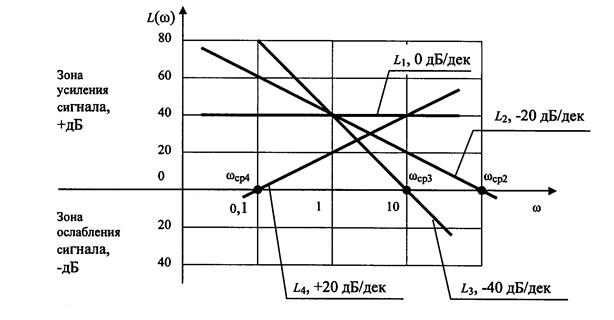
Рис.2.15

1) А1(w)=k1 ,

L1 (w ) = 20lg A1(w) = 20lg k1; пусть k1=100, тогда L(w) = 20lg100 = 40дБ.

В этом случае ЛАЧХ имеет вид прямой, параллельной оси абсцисс с ординатой 40дБ и наклоном 0 дБ/дек.

2) A2 (w)=k2/w, где k2=100

L₂ w)= 20lg A 2 (w ) = 20lg k2/w=20lg k 2-20lgw .

Отсюда видно, что ЛАЧХ представляет собой прямую, падающую при увеличении w, причем коэффициент наклона прямой составляет -20дБ на 1 декаду (единичный отрицательный наклон ЛАЧХ).

3) A₃ (w)=k3/w²,

L₃ (w) = 20lg k₃ - 20lgw² = 20lg k₃ - 40lgw .

Видно, что имеем ЛАЧХ – прямую с наклоном -40дБ/дек (двойной отрица-

тельный наклон).

4) A₄(w) = k₄w , где k4=10

L₄ (w) = 20lg k₄ + 20lgw .

Здесь имеем ЛАЧХ – прямую с наклоном +20дБ/дек (положительный единичный наклон).

ЛАЧХ в примерах 2), 3), 4) можно построить по двум точкам, определив L(w) на какой-либо частоте, а также определив частоту среза w_ср при L(w)=0.

Конкретный вид ЛАЧХ зависит от числа и типа элементов, составляющих САУ. Более подробно построение ЛАЧХ и их использование рассматривается в последующих разделах (3.5, 4.1, 4.2, 4.3 и т.д.).

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Определение частотных характеристик САУ.

2. Годограф АФЧХ.

3. Графическое отображение АЧХ, ФЧХ, ВЧХ, МЧХ.

4. Нахождение частотных характеристик по ПФ САУ.

5. Построение ЛАЧХ и ЛФЧХ.

6. Построение асимптотической ЛАЧХ.

ЛЕКЦИЯ № 6

ФОРМЫ ПРЕДСТАВЛЕНИЯ МОДЕЛЕЙ

Системный подход в анализе БСУ предполагает рассмотрение следующих моделей: структурной (морфологической), функциональной и информационной моделей (описания) системы.

Структурная (морфологическая) модель (СМ) системы - это модель, описывающая структуру системы, т.е. совокупность элементов, входящих в систему, и связей между ними. Морфологические свойства системы существенно зависят от характера связей. При этом выделяют информационные, энергетические и вещественные связи (см.п. 6 свойств БСУ в разделе 2.1.).

Функциональная модель системы (ФМ) - это модель, описывающая изменение состояния (поведения) системы во времени. Здесь состояние - это множество существенных свойств, которыми обладает система в данный момент времени.

Информационное описание (модель) системы должно характеризовать информационные процессы, протекающие в системе управления, должно давать представление о зависимости функциональных и морфологических свойств системы от количества и качества внутренней и внешней информации, о потоках информации, циркулирующих в системе, и их параметрах.

Методология системного подхода ориентирует на рассмотрение всех описаний (моделей) системы, на раскрытие её целостности, на выявление многообразных типов связей сложного объекта и сведения их в единую теоретическую картину.

Задача структурного анализа (моделирования) БСУ - определение оптимальной структуры (совокупности элементов и связей между ними) системы по выбранному критерию эффективности. Он является основой для выбора вновь синтезируемых вариантов БСУ, а также для усовершенствования уже созданных.

Построение структуры БСУ заключается в выделении элементов структуры, решающих определенные задачи, из общего объема функций БСУ. В основе выделения лежит принцип объединения в одном элементе функций, наиболее связанных информационно и функционально.

Структурный анализ БСУ должен позволить:

- выделить элементы системы, существенные для ее функционирования и управления;

- определить структуру системы и распределения задач по элементам;

- оптимизировать связи (информационные потоки) системы;

- оценить качество структуры, а в некоторых случаях и оптимизировать её уменьшением числа элементов и связей, сокращением излишней информации и т.п.

Решение этих задач с применением математических моделей и средств вычислительной техники требует соответствующих средств формализации.

Наиболее часто здесь используется математический аппарат теории графов. В этом случае элементы структуры располагаются в вершинах неориентированного графа, а ребра определяют отношения между ними (рис.1).

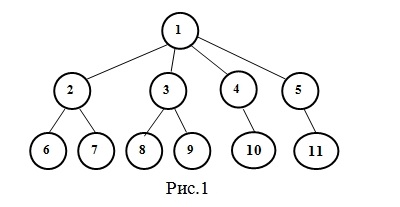
Для предварительной оценки структур на ранних стадиях проектирования применяются структурно-топологические характеристики БСУ, которые позволяют предварительно отобрать наиболее эффективные варианты структур.

Более подробно определение структурно-топологических характеристик БСУ рассмотрим в расчетно-графической работе.

Далее для более точной оценки структур используются алгоритмы, которые могут быть представлены целевыми функциями принятых критериев с учетом заданных ограничений. Целевая функция здесь обычно представляет систему зависимостей критерия оптимальности от наиболее существенных характеристик и параметров системы. Это позволяет, наряду с составом элементов и направленностью их взаимодействия, учитывать при решении задач другие стороны функционирования БСУ (временные, надежностные, стоимостные).

Функциональный анализ (ФА) выполняется после выполнения структурного проектирования БСУ, когда выделены элементы и структурная конфигурация, существенные для работы системы и управления ею, определены потоки информации, циркулирующие в системе.

Основная задача ФА - определение функциональных свойств и особенностей поведения БСУ, степень их соответствия целям создания системы. Реально ФА в зависимости от потребностей практики может включать большое число вопросов, связанных с поведением системы и ее отдельных элементов при управлении и воздействиях внешней среды.

К числу таких вопросов могут относиться исследования временных показателей (производительность, пропускная способность, реакция системы), определение характеристик надежности, поведения в критических ситуациях и т.п.