Частотные характеристики сау
Частотными характеристиками называются зависимости, характеризующие реакцию звена на гармоническое входное воздействие в установившемся режиме, т.е. вынужденные синусоидальные колебания звена. Частотные характеристики, определяют зависимость между амплитудой и фазой входного и выходного гармонических сигналов при изменении частоты входного сигнала.
Если на вход линейного звена подать гармоническое воздействие:
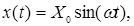
где X0 - амплитуда,
ω - угловая частота, имеющая размерность [рад/с] или [c-1],
то на выходе звена в установившемся режиме будет также гармоническая функция той же частоты, но другой амплитуды Y0 и сдвинутая по фазе относительно входной величины на угол ψ:
.
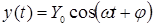Связь между выходной гармоникой и входной устанавливается с помощью частотной передаточной функции звена W(jω).
Частотная передаточная функция представляет собой отношение изображений по Фурье выходного и входного сигналов при нулевых начальных условиях и равных нулю воздействиях на остальных входах:
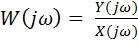(2.11)
Из сравнения преобразований Фурье и Лапласа следует, что частотную передаточную функцию звена легко получить из его передаточной функции путем замены s на jω(подстановка Фурье), т.е.
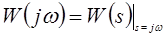
Запись W( jω) означает, что в передаточную функцию W(s) подставляется чисто мнимое число s = jω , где j =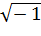 
.
Зависимость отношения амплитуды выходного сигнала к амплитуде входного сигнала при фиксированной частоте называют амплитудной частотной характеристикой (сокращенно - АЧХ) и обозначают А(w).
Сдвиг фаз между входным и выходным сигналами при фиксированной частоте называют фазовой частотной характеристикой (ФЧХ) и обозначают j(w).
Амплитудная фазовая частотная характеристика (АФЧХ) строится на комплексной плоскости в полярных координатах и представляет собой геометрическое место концов векторов (годографов), соответствующих частотной передаточной функции W(jω) при изменении частоты от нуля до бесконечности (рис.2.8). Полученные точки соединяются затем плавной кривой. АФЧХ строится как для положительных, так и для отрицательных частот. При замене в W(jω) ω на -ω получается сопряженная комплексная величина. Поэтому АФЧХ для отрицательных частот является зеркальным отображением относительно вещественной оси АФЧХ для положительных частот. На рис.2.8 АФЧХ для отрицательных частот показана пунктирной линией. Как видим, (АФЧХ) при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси абсцисс.
Длина вектора, проведенного из начала координат в точку АФЧХ, соответствующую выбранной частоте ω, равна А(ω), т.е показывает амплитуду выходного сигнала,. а угол между вектором и положительным направлением вещественной оси равен ψ(ω)- сдвиг фазы между выходным и входным сигналом.
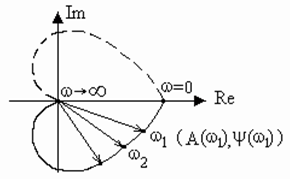
Рис.2.8
Частотная передаточная функция W(jw) представляет собой функцию комплексного переменного jw, модуль которой равен А(w), а аргумент равен j(w).
W(jw), как комплексная величина, может быть также представлена на комплексной плоскости. Здесь при её построении по осям координат в декартовых координатах (U, V), (ось абсцисс - Re и ось ординат - Im) откладывают соответственно значения вещественной и мнимой частей частотной передаточной функции звена.
Проекции вектора W(jw) на действительную и мнимую оси называют соответственно вещественной и мнимой частотными характеристиками и обозначают:
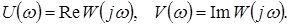
Отсюда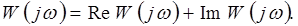 
(2.12)
Связь между вещественной и мнимой частотными функциями следующая:
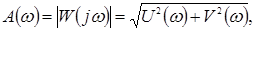(2.16)
Формула фазового сдвига имеет вид:
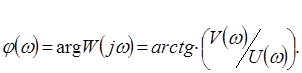(2.17)
Иногда фазовую частотную функцию обозначают буквой – f. Тогда из рис. 2.8следует, что упрощенными правильными формулами связывающими модуль частотной передаточной функции (A), фазовый сдвиг (f), вещественную (U) и мнимую (V) части частотной передаточной функции являются:
; 
; 
; 
.
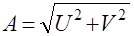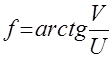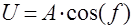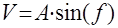Амплитудная частотная характеристика показывает, как пропускает звено сигналы различной частоты, иначе, представляет собой коэффициент изменения амплитуды гармонических колебаний при прохождении через звено.
Для построения амплитудно-частотной характеристики необходимо найти амплитуду выходного сигнала.
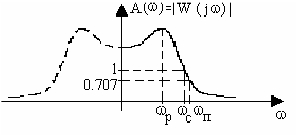АЧХ при ее определении в диапазоне частот от минус бесконечности до плюс бесконечности симметрична относительно оси ординат (рис. 2.9),
Рис. 2.9.
На рис. 2.9:
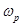- резонансная частота, т.е. частота, на которой амплитудная частотная характеристика достигает максимума, иначе, на этой частоте звено имеет максимальный коэффициент усиления;
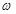с - частота среза, частота, на которой амплитудная частотная характеристика, уменьшаясь, принимает значение, равное единице, и при дальнейшем повышении частоты остается меньше единицы;
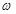п - частота пропускания, частота, на которой амплитудная частотная характеристика, уменьшаясь, принимает значение, равное 0,707, и при дальнейшем повышении частоты не увеличивается;
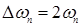- полоса пропускания, диапазон частот гармонических колебаний, пропускаемых звеном без заметного ослабления.
Фазовая частотная характеристика (ФЧХ) графически отображается графиком, показанным на рис 2.10.
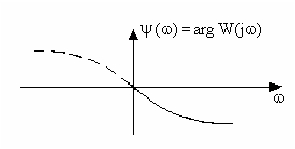
Рис. 2.10.
Вещественная частотная характеристика (ВЧХ). Представляет собой зависимость вещественной составляющей частотной передаточной функции от частоты(рис.2.11.)
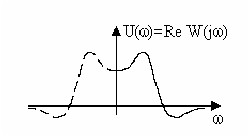
Рис. 2.11.
Мнимая частотная характеристика (МЧХ). Представляет собой зависимость мнимой составляющей частотной передаточной функции от частоты (рис.2.12). Симметрична относительно начала координат.
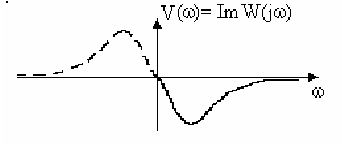
Рис. 2.12.
Часто возникает необходимость по заданной передаточной функции САУ определить те или иные частотные характеристики.
Пример. По заданной ПФ системы:
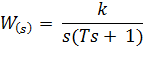
определить вещественную часть частотной передаточной функции. Обычно такая процедура выполняется следующим образом.
Подставляем s=jω, учитывая, что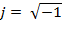 
, снижаем порядок j (j2 = -1 и т.п.), избавляемся от мнимости в знаменателе, умножая числитель и знаменатель дроби на комплексное выражение, сопряженное, стоящему в знаменателе, отделяем действительную и мнимую части, приводим в знаменателе подобные члены. Выделив действительную часть и, учитывая зависимость (2.14), получим вещественную часть частотной передаточной функции:
.
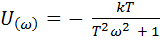Для определения модуля частотной передаточной функции, используя предыдущие вычисления и зависимость (2.16), получим:
.
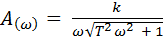