Мгновенная скорость прямолинейно движущейся точки
Пусть  – уравнение движения точки и
– уравнение движения точки и  – путь, пройденный точкой до фиксированного момента
– путь, пройденный точкой до фиксированного момента  , а
, а  – путь, пройденный точкой до момента
– путь, пройденный точкой до момента  . Найдем путь, пройденный точкой за время
. Найдем путь, пройденный точкой за время  :
:
 .
.
Средней скоростью  прямолинейного движения за время
прямолинейного движения за время  называется отношение пройденного пути к затраченному времени:
называется отношение пройденного пути к затраченному времени:
 .
.
Если существует предел  при
при  , он называется мгновенной скоростью в момент
, он называется мгновенной скоростью в момент  :
:
 .
.
К нахождению пределов вида, в рассмотренных выше задачах, приводят решения и множества других задач. Можно показать, что:
· если  – количества электричества, проходящего через поперечное сечение проводника за время
– количества электричества, проходящего через поперечное сечение проводника за время  , то сила тока в момент времени
, то сила тока в момент времени  равна:
равна:
 ;
;
· если  – количества вещества, вступающего в химическую реакцию за время
– количества вещества, вступающего в химическую реакцию за время  , то скорость химической реакции в момент времени
, то скорость химической реакции в момент времени  равна:
равна:
 ;
;
· если  – масса неоднородного стержня между точками
– масса неоднородного стержня между точками  и
и  , то линейная плотность стержня в точке x0есть:
, то линейная плотность стержня в точке x0есть:
 ;
;
Все рассмотренные выше пределы имеют одинаковую математическую структуру и являются математическими моделями, которые характеризуют скорость изменения определенного процесса (зависимой величины) для каждого значения независимой величины: скорость изменения ординаты кривой (касательная кривой), скорость изменения пути от времени, скорость изменения заряда от времени и т.д.
С математической точки зрения все эти пределы одинаковы и отличаются только обозначениями. В математике зависимую и независимую величины принято обозначать y и x. Тогда возникает вопрос: как обозначить скорость изменения зависимой в определенном процессе величины (т.е. функции), в зависимости от аргумента.
В математике приняты следующие обозначения:
 - ввел Лейбниц;
- ввел Лейбниц;  - ввел Ньютон;
- ввел Ньютон; 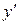 - ввел Лагранж.
- ввел Лагранж.
Таким образом, предел отношения приращения функции к приращению аргумента называют производной функции. Обозначается 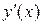 , читается «
, читается « 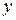 штрих по
штрих по 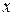 ».
».
Производная функции в точке
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  , где
, где 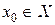 .
.
Чтобы найти производную функции в точке  , необходимо проделать следующие операции:
, необходимо проделать следующие операции:
- аргументу
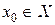 дадим приращение
дадим приращение 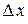 , т.е.
, т.е. 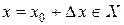 ;
; - найдем соответствующее приращение функции
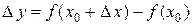 ;
; - составим отношение приращения функции к приращению аргумента
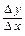 ;
; - найдем предел этого отношения при
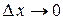 , т.е.
, т.е. 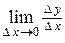
Если этот предел существует, то его называют производной функции  и обозначают:
и обозначают: 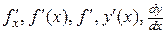 .
.
Определение 3.1. Производной функции  в точке
в точке  называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.
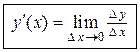 (3.1)
(3.1)
или
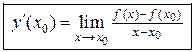 . (3.2)
. (3.2)
Нахождение производной функции  называется дифференцированием этой функции. Функция, имеющая производную в точке
называется дифференцированием этой функции. Функция, имеющая производную в точке  , называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках множества X, называется дифференцируемой на этом множестве.
, называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках множества X, называется дифференцируемой на этом множестве.
Значение производной функции  в точке
в точке  обозначается одним из символов:
обозначается одним из символов: 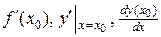 .
.
Пример 3.1. Найти значение производной функции  в точке
в точке  , используя определение производной функции:
, используя определение производной функции:
1) 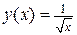 ,
, 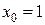 ; 3)
; 3) 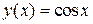 ,
, 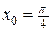 ;
;
2) 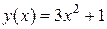 ,
, 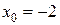 ; 4)
; 4) 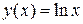 ,
, 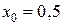 .
.
Решение. 1) I способ: используем формулу 1.2:
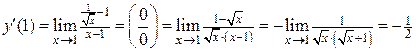 .
.
II способ: используем формулу 1.1:
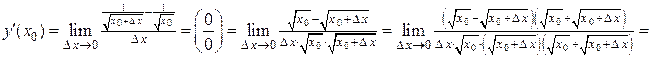
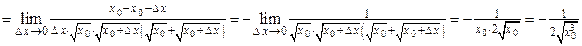 .
.
Таким образом,
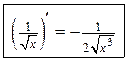 .
.
Находим значение производной функции в точке 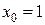 :
:
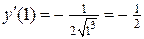 .
.
2) Воспользуемся формулой 3.1:
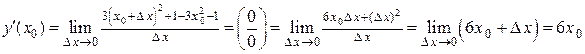 .
.
Таким образом,
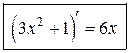 .
.
Находим значение производной функции в точке 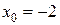 :
:
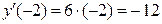 .
.
3) Воспользуемся формулой 3.1:
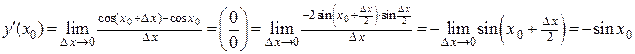
Таким образом,
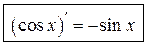 .
.
Находим значение производной функции в точке 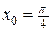 :
: 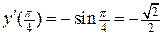 .
.
4) Воспользуемся формулой 3.1:
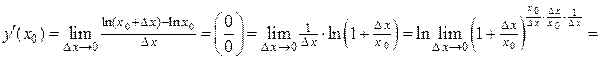
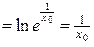 .
.
Таким образом,
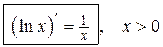 .
.
Находим значение производной функции в точке 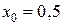 :
: 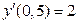 .
.
,
Выше была рассмотрена задача про касательную к кривой, в которой был найден угловой коэффициент касательной:
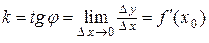 .
.
Это дает возможность сформулировать геометрический смысл производной функции в точке: производная 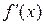 в точке
в точке  равна угловому коэффициенту касательной к графику функции
равна угловому коэффициенту касательной к графику функции  в точке, абсцисса которой равна
в точке, абсцисса которой равна  :
:
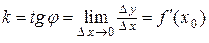 .
.
Механический смысл: скорость прямолинейного движения материальной точки в момент время 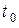 есть производная от пути
есть производная от пути 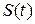 по времени
по времени 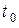 :
:
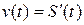 .
.
Физический смысл: если функция  описывает какой-либо процесс, то производная
описывает какой-либо процесс, то производная 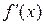 есть скорость протекания этого процесса.
есть скорость протекания этого процесса.
3.3.Связь между непрерывностью и
Дифференцируемостью функции
Определяя понятие производной функции в точке  , мы предполагали лишь существование функции в точке
, мы предполагали лишь существование функции в точке  и в некоторой достаточно малой ее окрестности, и существование предела
и в некоторой достаточно малой ее окрестности, и существование предела 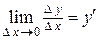 . Теперь свяжем дифференцируемость функции в точке с непрерывностью этой функции.
. Теперь свяжем дифференцируемость функции в точке с непрерывностью этой функции.
Теорема 3.1. Если функция  определена на X и в точке
определена на X и в точке 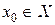 имеет конечную производную
имеет конечную производную 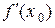 , то
, то 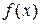 непрерывна в точке
непрерывна в точке  .
.
Из теоремы 3.1. следует, что в точках разрыва функции  производная не существует.
производная не существует.
Неверно утверждение, обратное к теореме 3.1.: из непрерывности функции в точке не следует существование производной в этой точке.
Например, функция 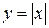 в точке
в точке 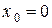 непрерывна, но производная не существует, т.к.
непрерывна, но производная не существует, т.к.
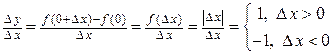 .
.
Это значит, график функции не имеет касательной в точке 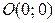 .
.
Хотя 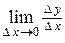 для функции
для функции 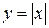 не существует, но существуют односторонние пределы:
не существует, но существуют односторонние пределы: 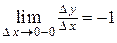 и
и 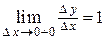 . В этом случае говорят, что функция имеет односторонние производные.
. В этом случае говорят, что функция имеет односторонние производные.
Односторонними производными (производными слева и справа) называют 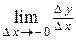 и
и 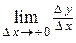 , если они существуют. Обозначаются соответственно:
, если они существуют. Обозначаются соответственно: 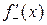 и
и 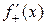 .
.
Если 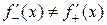 , то производная в точке не существует.
, то производная в точке не существует.
Надо заметить, что производная 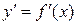 непрерывной функции
непрерывной функции  сама не обязательно является непрерывной.
сама не обязательно является непрерывной.
Например, функция 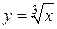 определена для
определена для 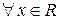 , т.е.
, т.е. 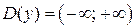 . По определению 3.1.
. По определению 3.1. 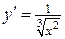 . В точке
. В точке 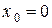 производная функции равна
производная функции равна 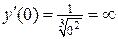 , хотя сама функция в точке
, хотя сама функция в точке 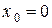 непрерывна.
непрерывна.
Если 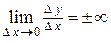 , то производная называется бесконечной.
, то производная называется бесконечной.
Если функция  имеет непрерывную производную
имеет непрерывную производную 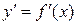 в некотором интервале
в некотором интервале 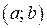 , то функция называется гладкой.
, то функция называется гладкой.
3.4.Основные правила дифференцирования.
