Деление на наибольшую степень
Предел отношения двух многочленов (при условии, что аргумент стремится к ∞) равен пределу отношения их старших членов.

Примеры:
1. найти 
Решение:
Имеем неопределённость вида 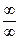 . Для раскрытия неопределённости разделим почленно числитель и знаменатель на наивысшую степень x, т.е. на x3, предварительно раскрыв скобки.
. Для раскрытия неопределённости разделим почленно числитель и знаменатель на наивысшую степень x, т.е. на x3, предварительно раскрыв скобки.

Ответ: 
2. Найти 
Решение:
Имеем неопределённость вида 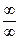 . Для раскрытия неопределённости разделим почленно
. Для раскрытия неопределённости разделим почленно
числитель и знаменатель на наивысшую степень x, т.е. на x4 .
 Ответ:
Ответ: 
Замена переменной
Пример:
Найти 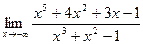
Решение:
Имеем неопределённость вида 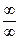 . Для раскрытия неопределённости сделаем замену x=−t (t=-x, t→+∞ при x→−∞), а затем разделим почленно числитель и знаменатель на наивысшую степень t, т.е. на t5.
. Для раскрытия неопределённости сделаем замену x=−t (t=-x, t→+∞ при x→−∞), а затем разделим почленно числитель и знаменатель на наивысшую степень t, т.е. на t5.
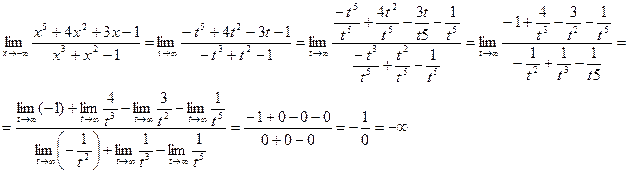 Ответ:
Ответ: 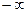
3.4. Неопределенность вида 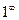
Применение второго замечательного предела
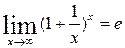 ;
; 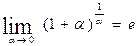
Пример:
Найти 
Решение:
 - неопределенность.
- неопределенность.
Т.к  , то неопределенность вида
, то неопределенность вида  .
.
Для ее раскрытия применим 2-й замечательный предел: 
а) Выделим из дроби  целую часть:
целую часть:

а) заменим  , чтобы дробь
, чтобы дробь  приняла вид
приняла вид 
в) для выражения предела А через новую переменную «n» необходимо найти (2x-2) и выяснить к какому значению стремится «n»:
Т.к  , то 2x-1=6n и
, то 2x-1=6n и 
2x=6n+1
2x-2=6n+1-2
2x-2=6n-1
Т.к  , то n
, то n 

Т.о 
г) Разложим данный предел по свойствам предела и степени:
 и вычислим предел
и вычислим предел

Ответ: 
3.5. Неопределенность вида 
Сведение данной неопределенности с помощью равносильных преобразований к неопределенностям вида 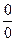 или
или  .
.
Пример.
Найти 
Решение:

Применим правило Лопиталя

Ответ. 
IV. АСИМПТОТЫ КРИВОЙ
Прямая называется асимптотой кривой y=f(x), если расстояние от точки М(x;y) до этой прямой стремится к 0 при стремлении хотя бы одной из координат к ∞
Вертикальные асимптоты.
График функции 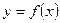 при
при 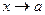 имеет вертикальную асимптоту, если
имеет вертикальную асимптоту, если 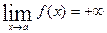 или
или 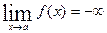 ; при этом точка
; при этом точка 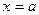 есть точка разрыва II-го рода. Уравнение вертикальной асимптоты имеет вид
есть точка разрыва II-го рода. Уравнение вертикальной асимптоты имеет вид 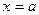 .
.
Горизонтальные асимптоты.
График функции 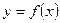 при
при 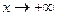 или при
или при 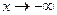 имеет горизонтальную асимптоту, если
имеет горизонтальную асимптоту, если 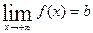 или
или 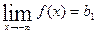 . Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид
. Может оказаться, что либо только один из этих пределов конечный, либо ни одного. Тогда график имеет или одну горизонтальную асимптоту, или ни одной. Уравнение горизонтальной асимптоты имеет вид 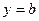 (рис. 9).
(рис. 9).

Рис. 9. Графики функций, имеющие горизонтальные асимптоты
Наклонные асимптоты.
Если существуют пределы 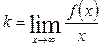 и
и 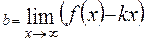 , то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x→
, то прямая y=kx+b является наклонной асимптотой кривой при указанном стремлении x. При x→ 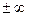 асимптоты могут быть различны.
асимптоты могут быть различны.
V. ПРИМЕРЫ ИССЛЕДОВАНИЯ ФУНКЦИЙ
Примеры:
1. 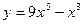
1) D(y)=R, E(y)=R (находим по графику)
2) Непрерывность. Асимптоты.
Так как функция 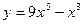 является элементарной, то она непрерывна в каждой точке своей области определения, т.е. на всей числовой прямой. Выясним поведение функции на концах области определения.
является элементарной, то она непрерывна в каждой точке своей области определения, т.е. на всей числовой прямой. Выясним поведение функции на концах области определения.

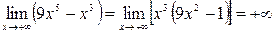
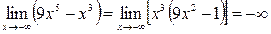
Асимптот нет.
3) Четность.
Так как область определения функции симметрична относительно нуля, выясним, имеют ли место следующие равенства:
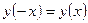 или
или 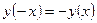 .
.
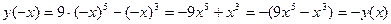
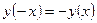 .
.
Следовательно, функция является нечётной. Её график симметричен относительно начала координат.
4) Функция не является периодической.
5) Нули функции
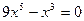
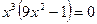
или 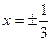
(0;0); 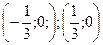 - точки пересечения графика с осями.
- точки пересечения графика с осями.
6) Монотонность функции. Экстремумы функции.
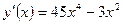
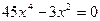
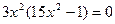
x=0 , 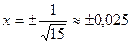
| x | 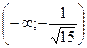 | 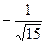 | 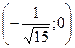 | 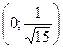 | 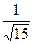 | 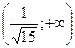 | |
| y` | + | _ | _ | + | |||
| y |  | 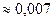 |  |  | -0,007 |  |
max min
7) Выпуклость. Точки перегиба.
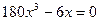
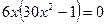
x=0 или 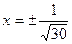
| x | 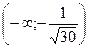 | 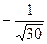 | 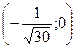 | 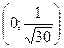 | 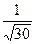 | 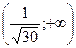 | |
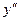 | _ | + | _ | + | |||
| y | 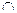 | 0,004 |  |  | -0,004 |  |
т. перегиба т. перегиба т. перегиба
8) График
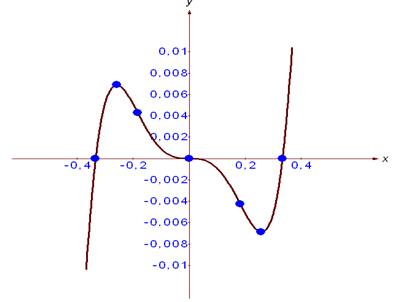
2. 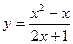
1) 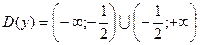 , E(y)=
, E(y)= 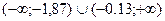 (определяем в конце задания после построения графика функции).
(определяем в конце задания после построения графика функции).
2) Непрерывность. Асимптоты.
Данная функция определена при всех значениях 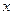 , кроме
, кроме 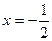 . Так как функция
. Так как функция 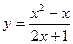 является элементарной, то она непрерывна в каждой точке своей области определения. Таким образом, единственной точкой разрыва служит точка
является элементарной, то она непрерывна в каждой точке своей области определения. Таким образом, единственной точкой разрыва служит точка 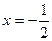 . Для исследования характера разрыва найдем левый и правый пределы функции при
. Для исследования характера разрыва найдем левый и правый пределы функции при 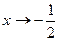 .
.
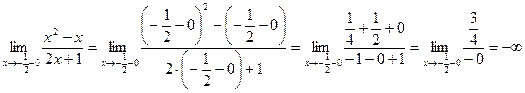 .
.
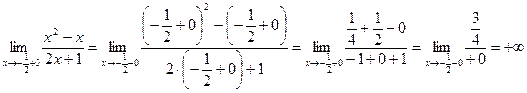 .
.
Следовательно, функция 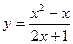 в точке
в точке 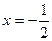 имеет бесконечный разрыв, т.е.
имеет бесконечный разрыв, т.е. 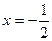 - точка разрыва II-го рода.
- точка разрыва II-го рода. 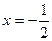 - вертикальная асимптота.
- вертикальная асимптота.
Найдем наклонные асимптоты.
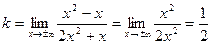
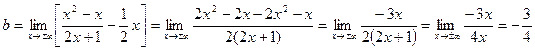
Итак, 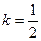 и
и 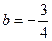 . Следовательно, при
. Следовательно, при 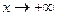 и при
и при 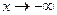 график функции имеет наклонную асимптоту
график функции имеет наклонную асимптоту 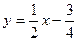 .
.
3) Четность.
Область определения не симметрична относительно нуля, поэтому функция не является ни четной, ни нечетной.
4) Функция не является периодической.
5) Нули функции.
y=0 , если x2-x=0; x(x-1)=0; x1=0 или x2=1
(0; 0), (1; 0) – точки пересечения графика с осями координат.
6) Монотонность. Точки экстремума.
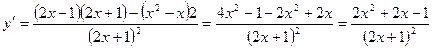
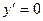 , если 2x2+2x-1=0
, если 2x2+2x-1=0
2x2+2x-1=0
D=4+8=12
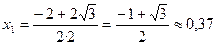
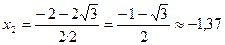
| x | 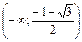 | 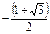 | 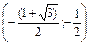 | 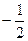 | 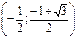 | 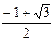 | 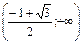 |
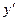 | + | _ | - | _ | + | ||
| y |  | 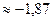 |  | - |  | -0,13 |  |
max min
7) Выпуклость. Точки перегиба.
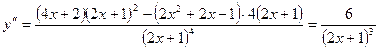
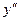 не существует при
не существует при 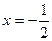
| x | 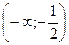 | 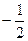 | 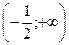 |
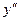 | _ | - | + |
| y | 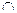 | - | 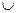 |
Точек перегиба нет
8) График
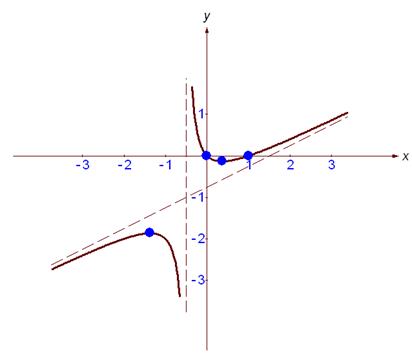
3. 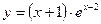
1) D(y)=R, E(y)= 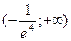 (определяем в конце задания после построения графика функции).
(определяем в конце задания после построения графика функции).
2) Непрерывность. Асимптоты.
Функция непрерывна на всей числовой прямой. Точек разрыва нет. Следовательно, вертикальных асимптот нет.
Исследуем поведение функции на концах области определения.
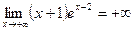
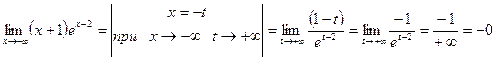
При 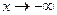
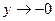 . Следовательно, при
. Следовательно, при 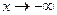 функция имеет горизонтальную асимптоту
функция имеет горизонтальную асимптоту 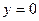
3) Четность.
Область определения не симметрична относительно нуля, поэтому функция не является ни четной, ни нечетной.
4) Функция не является периодической.
5) Нули функции.
y=0, если x=-1
Если x=0, то 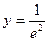
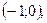
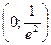 - точки пересечения с осями.
- точки пересечения с осями.
6) Монотонность. Экстремумы функции.
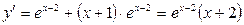
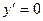 , если x = -2 - критическая точка
, если x = -2 - критическая точка
| x | 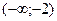 | -2 | 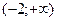 |
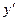 | _ | + | |
| y |  | 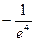 |  |
min
7) Выпуклость. Точки перегиба.
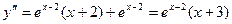
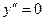 , если x=-3
, если x=-3
| x | 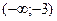 | -3 | 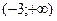 |
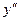 | _ | + | |
| y | 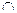 | 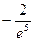 | 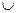 |
т. перегиба
8)
VI. ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОПРОВЕРКИ
1. Что такое функция?
2. Какая функция называется бесконечно малой, бесконечно большой?
3. Какова связь между бесконечно малой и бесконечно большой функциями?
4. Сформулируйте основные теоремы о пределах.
5. Дайте определение непрерывной функции в точке и на промежутке.
6. Сформулируйте необходимый и достаточный признаки убывания (возрастания) функции на интервале.
6. Что называется экстремумом функции на интервале?
7. Сформулируйте необходимое и достаточное условие существования экстремума.
8. Дайте определения выпуклости и вогнутости кривой на интервале.
9. Что называется точкой перегиба графика функции? Алгоритм нахождения точек перегиба.
10. Сформулируйте достаточный признак существования точки перегиба.
11. Изложите общую схему исследования функции и построения ее графика.
Найти пределы:
1. 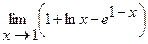 | 2. 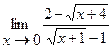 |
3. 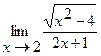 | 4. 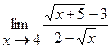 |
5. 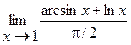 | 6. 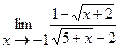 |
7. 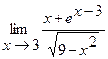 | 8. 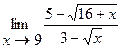 |
9. 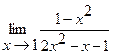 | 10. 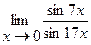 |
11. 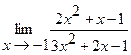 | 12. 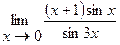 |
13. 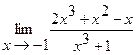 | 14. 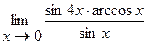 |
15. 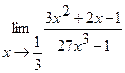 | 16. 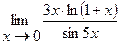 |
17. 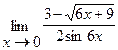 | 18. 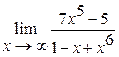 |
19. 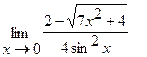 | 20. 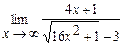 |
21. 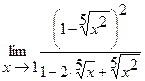 | 22. 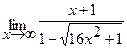 |
23 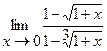 | 24. 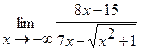 |
25. 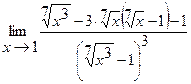 | 26. 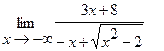 |
27. 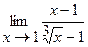 | 28. 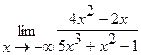 |
29. 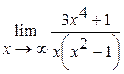 | 30. 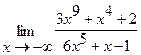 |
VII. ЗАДАНИЯ ДЛЯ ДОМАШНЕЙ РАСЧЕТНО-ГРАФИЧЕСКОЙ РАБОТЫ ПО ТЕМЕ:
«ИССЛЕДОВАНИЕ ФУНКЦИИ И ПОСТРОЕНИЕ ЕЕ ГРАФИКА»
№1 1. 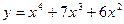 2. 2. 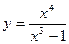 3. 3. 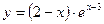 | №2 1. 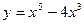 2. 2. 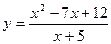 3. 3. 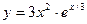 |
№3 1. 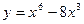 2. 2. 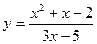 3. 3. 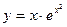 | №4 1. 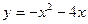 2. 2.  3. 3.   |
№5 1.  2. 2.  3. 3.  | №6 1.  2. 2.  3. 3.  |
№7 1.  2. 2.  3. 3.  | №8 1.  2. 2.  3. 3.  |
№9 1.  2. 2.  3. 3.  | №10 1.  2. 2.  3. 3.  |
№11 1.  2. 2.  3. 3.  | №12 1.  2. 2.  3. 3.  |
№13 1.  2. 2.  3. 3.  | №14 1.  2. 2.  3. 3.  |
№15 1.  2. 2.  3. 3.  | №16 1.  2. 2.  3. 3.   |
№17 1.  2. 2.  3. 3.  | №18 1.  2. 2.  3. 3.  |
№19 1.  2. 2.  3. 3.  | №20 1.  2. 2.  3. 3.  |
№21 1.  2. 2.  3. 3.  | №22 1.  2. 2.  3. 3.  |
№23 1.  2. 2.  3. 3.  | №24 1.  2. 2.  3. 3.  |
VIII. ПРИМЕРНЫЕ ВАРИАНТЫ ТЕСТОВ
1. Функция  называется бесконечно малой, если
называется бесконечно малой, если
a). 
b). 
c). 
d). 
2 Предел  равен
равен
a). 0
b). 1
c). -3
d). 4
3. Предел  равен
равен
a). ∞
b). 0
c). 1
d). -∞
4 Предел  равен
равен
a). 4
b). -1
c). 
d). 2
5 Предел  равен
равен
a). 
b). 
c). 3
d). 4
6 Предел  равен
равен
a). -5
b). 2
c). 0,3
d). 0
7. Производная функции  имеет вид
имеет вид
a) 
b) 
c) 
d) 
8. На рисунке изображён графc)ик функции 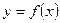 и касательная к нему в тоd)чке с абсциссой
и касательная к нему в тоd)чке с абсциссой  .d)
.d)
Найдите значение производной функции 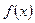 в точке
в точке  .
.

a) -1
b) -0,5
c) -2
d) -0,25
9.На рисунке изображён график производной функции 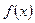 , определённой на интервале (-7; 5). Найдите точку экстремума функции
, определённой на интервале (-7; 5). Найдите точку экстремума функции 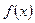 , принадлежащих отрезку [-6; 4]
, принадлежащих отрезку [-6; 4]

a) -1
b) -3
c) -2
d) -4
10 Если при переходе аргумента слева направо через точку  производная
производная  меняет знак с — на + , то функция
меняет знак с — на + , то функция
a) имеет максимум
b) имеет точку перегиба
c) имеет минимум
d) не определена
ЛИТЕРАТУРА
1. Зайцев, И. А. Высшая математика: учебник / И. А. Зайцев. – 3-е изд., испр. - М.: Дрофа, 2004. – 400 с.
2. Данко, П.Е. Высшая математика в упражнениях и задачах: учеб. пособие / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова, С.П. Данко. – М. : Оникс, 2008. – 816 с.
3. Кудрявцев, В. А. Краткий курс высшей математики: учеб. пособие / В.А. Кудрявцев, Б. П. Демидович. - М. : АСТ, 2008. – 654с.
4. Минорский, К. П. Сборник задач по высшей математике: учеб. пособие /
К. П. Минорский. - 15-е изд.–М. : Физматлит, 2008. – 336 с.
5. Письменный, Д.Т. Конспект лекций по высшей математике: ( в2 ч.) Ч.1 / Д. Т. Письменный. - 7-е изд.–М. : Айрис-пресс, 2007. – 288 с.
СОДЕРЖАНИЕ
Введение. 3
I. Функция. Свойства функции. 4
Ii. Предел функции. Непрерывность функции. 9
III. Методы раскрытия неопределенностей. 13
IV. Асимптоты кривой. 23
V. Примеры исследования функций. 24
VI. Вопросы и задачи для самопроверки. 29
VII. Задания для домашней расчетно-графической работы по теме: 31
«исследование функции и построение ее графика». 31
VIII. Примерные варианты тестов. 34
Литература. 37
