По выполнению курсового проекта
УТВЕРЖДАЮ
Декан технологического факультета
_______________О.И. Борискин
"___" _____________ 20__г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
По выполнению курсового проекта
дисциплины
«МЕТРОЛОГИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОДУКЦИИ,
ПРОЦЕССОВ И УСЛУГ»
Направление подготовки: 200500
«Метрология, стандартизация и сертификация»
Специальность: 200501 «Метрология и метрологическое обеспечение»
Форма обучения: очная
Тула 2009
Методические указания составлены профессором Е.Н. Валиковым, ассистентом В.А. Беляковой и обсуждены на заседании кафедры «Инструментальные и метрологические системы» технологического факультета,
протокол № от 20___г.
Заведующий кафедрой ______________О.И. Борискин
Методические указания пересмотрены и утверждены на заседании кафедры «Инструментальные и метрологические системы» технологического факультета,
протокол № от 20___г.
Заведующий кафедрой ______________О.И. Борискин
Аннотация
Пояснительная записка включает в себя семь пунктов.
В первом пункте на основании исходных данных определены показатели точности зубчатых колес в соответствии с требованиями стандарта и разработаны рабочие чертежи зубчатых колес пары.
Во втором пункте произведен статистический анализ точности технологического процесса посредством больших выборок.
В третьем пункте произведен корреляционно-регрессионный анализ зависимости между двумя переменными на примере исследования влияния погрешности колебания длины общей нормали цилиндрического зубчатого колеса после зубофрезерования на колебание длины общей нормали цилиндрического зубчатого колеса после шевингования-прокатывания.
В четвертом пункте выполнен расчет прямолинейного уравнения регрессии и коэффициента корреляции при ограниченном числе опытов.
В пятом пункте рассмотрена криволинейная корреляционная связь, в качестве которой выбрана параболическая связь.
В шестом пункте рассмотрена множественная корреляция на примере линейной корреляционной связи между тремя величинами.
В заключительном седьмом пункте проведено исследование точности измерения линейного размера.
Содержание
| Задание 1. Нахождение показателей точности цилиндрических зубчатых колес и оформление чертежей……………………………………….. | |
| Задание 2.Статистический анализ точности технологическогопроцесса посредством больших выборок…………………………………….. | |
| Задание 3.Корреляционно-регрессионный анализ зависимости между двумя переменными……………………………………………………….. | |
| Задание 4.Расчет прямолинейного уравнения регрессии и коэффициента корреляции при ограниченном числе опытов……………………… | |
| Задание 5.Криволинейная корреляционная связь………………………. | |
| Задание 6.Множественная корреляция………………………………….. | |
| Задание 7.Исследование точности измерения линейного размера……. |
ЗАДАНИЕ 1
ЗАДАНИЕ 2
Статистический анализ точности технологического
ЗАДАНИЕ 3
Корреляционно-регрессионный анализ зависимости
Между двумя переменными
Корреляционно-регрессионный анализ зависимости между двумя переменными состоит из пяти этапов:
1. Проведение эксперимента.
2. Предварительная обработка результатов эксперимента и составление корреляционной таблицы.
3. Расчет коэффициента корреляции и корреляционного отношения.
4. Проверка гипотезы равенства коэффициента корреляции корреляционному отношению.
5. Анализ модели.
Проведение анализа рассмотрим на примере исследования влияния погрешности колебания длины общей нормали цилиндрического зубчатого колеса после зубофрезерования на колебание длины общей нормали цилиндрического зубчатого колеса после шевингования-прокатывания.
1. Проведение эксперимента.
Отберем партию заготовок (50 штук) и пронумеруем их. На всех заготовках проставим клеймо с номером. Выполним первую операцию - обработаем заготовки на зубофрезерном станке. Измерим колебание длины общей нормали на универсальном зубоизмерительном приборе фирмы «Карл Кцейс» с помощью оправки и индикаторной головки с ценой деления 0,001 мм. Затем партию заготовок обработали на чистовой операции шевингование-прикатывание. После чистовой обработки проводится измерение колебания длины общей нормали на том же приборе. После второй операции измерение должно происходить в строгой последовательности согласно маркировке. По результатам измерений составляется таблица 1.
Таблица 1 - Результаты измерения колебания длины общей нормали
| № п/п | 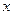 | 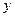 | № п/п | 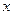 | 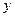 | № п/п | 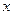 | 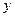 | № п/п | 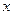 | 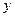 | № п/п | 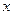 | 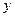 |
2. Предварительная обработка результатов эксперимента.
Используя таблицу 1, результаты измерений разбиваем на интервалы. Для этого находим минимальное и максимальное значения величин параметров после первой операции ( 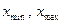 ) и после второй операции (
) и после второй операции ( 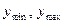 ). Определим размах варьирования:
). Определим размах варьирования:
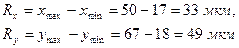
Задаемся числом интервалов 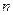 . Для количества наблюдений
. Для количества наблюдений 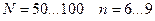 . Примем
. Примем
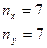
Определим цену интервалов
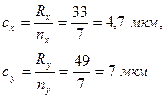
Принимаем
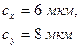
Полученные величины интервалов 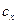 и
и 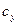 больше цены деления средств измерения (1 мкм), что удовлетворяет установленным требованиям.
больше цены деления средств измерения (1 мкм), что удовлетворяет установленным требованиям.
Таблица 2
| № интервала | Интервал 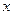 | Середина 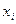 | № интервала | Интервал 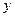 | Середина 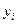 | |
| 13…19 | 14…22 | |||||
| 19…25 | 22…30 | |||||
| 25…31 | 30…38 | |||||
| 31…37 | 38…46 | |||||
| 37…43 | 46…54 | |||||
| 43…49 | 54…62 | |||||
| 49…55 | 62…70 |
Подсчитаем частоту попадания размеров по каждому интервалу в соответствии с таблицей 2.
Исходными данными для таблицы 2 являются результаты таблицы 1. Последовательность заполнения таблицы 2 следующая.
В таблице 1 записана под номером 1 величина 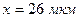 и
и 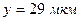 . В клетке таблицы 2, соответствующей интервалу
. В клетке таблицы 2, соответствующей интервалу 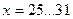 и
и 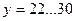 проставляется штриховая отметка. Для номера 2
проставляется штриховая отметка. Для номера 2 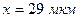 и
и 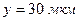 штриховая отметка ставится в клетку, соответствующую интервалу
штриховая отметка ставится в клетку, соответствующую интервалу 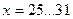 и
и 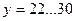 и так далее для всех пятидесяти номеров. В том случае, когда значение
и так далее для всех пятидесяти номеров. В том случае, когда значение 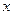 или
или 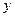 лежит на границе интервала, штриховая отметка заносится в клетку, соответствующую началу интервала.
лежит на границе интервала, штриховая отметка заносится в клетку, соответствующую началу интервала.
| Таблица 2 | 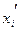 | -3 | -2 | -1 | |||||||||
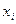 | 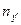 | 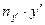 | 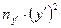 | ||||||||||
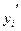 | 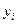 | 13-19 | 19-25 | 25-31 | 31-37 | 37-43 | 43-49 | 49-55 | |||||
| -3 | 14-22 | -21 | |||||||||||
| -2 | 22-30 | -22 | |||||||||||
| -1 | 30-38 | -6 | |||||||||||
| 38-46 | |||||||||||||
| 46-54 | |||||||||||||
| 54-62 | |||||||||||||
| 62-70 | |||||||||||||
| Таблица 3 | 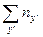 | 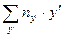 | 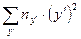 | ||||||||||
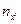 | 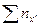 | ||||||||||||
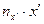 | -6 | -22 | -19 | 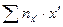 | -38 | -24 | |||||||
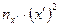 | 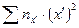 | ||||||||||||
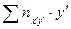 | -3 | -23 | -2 |  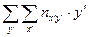 | -24 | ||||||||
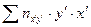 | -6 | 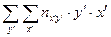 | |||||||||||
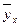 | -1,5 | -1,21 | 0,18 | 0,33 | -2 |
3. Расчет коэффициента корреляции и корреляционного отношения.
Для расчета коэффициента корреляции предварительно вычисляются следующие величины:
- математическое ожидание значений 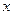 и
и 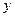
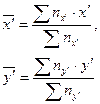
- среднее квадратическое отклонение от средней 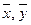
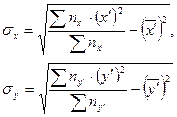
- коэффициент ковариации
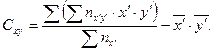
Тогда коэффициент корреляции будет равен
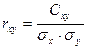
Корреляционное отношение вычисляется по формуле
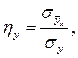
где 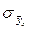 - СКО частной средней
- СКО частной средней 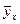 от общей средней
от общей средней 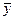 , равное
, равное
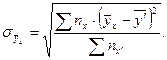
Для упрощения вычислений составляется корреляционная таблица 3, исходными данными для которой являются данные таблицы 2. В таблице 3 за новое начало отсчета приняты для 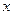 интервал 31-37 мкм, для
интервал 31-37 мкм, для 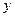 интервал 38-46 мкм. Введены новые переменные
интервал 38-46 мкм. Введены новые переменные 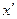 и
и 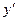 , с помощью которых можно существенно облегчить процедуру вычисления. Переход к новым переменным осуществляется по формулам:
, с помощью которых можно существенно облегчить процедуру вычисления. Переход к новым переменным осуществляется по формулам:
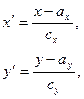
где 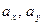 - новые начала отсчета (рекомендуется принимать средние интервалов). В данном примере
- новые начала отсчета (рекомендуется принимать средние интервалов). В данном примере 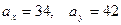 .
.
Новые значения интервалов отличаются один от другого на 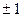 .
.
Таблица 3 отличается от таблицы 2 тремя графами и шестью строками. Порядок заполнения таблицы следующий. В графе 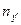 подсчитываются суммарные значения частот по интервалам
подсчитываются суммарные значения частот по интервалам 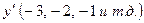 . Умножая эти значения графы на соответствующие значения интервалов
. Умножая эти значения графы на соответствующие значения интервалов 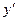 , получаем данные для заполнения клеток
, получаем данные для заполнения клеток 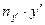 . Данные для заполнения клеток графы
. Данные для заполнения клеток графы 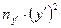 получены путем перемножения данных предыдущей графы на соответствующий интервал
получены путем перемножения данных предыдущей графы на соответствующий интервал 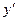 .
.
Аналогично заполняются клетки строк 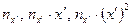 . В каждой клетке четвертой строки сумма
. В каждой клетке четвертой строки сумма 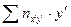 записывается как сумма произведений частот
записывается как сумма произведений частот 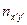 на соответствующие значения
на соответствующие значения 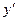 . Например, для
. Например, для 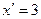 сумма
сумма 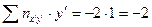 , для
, для 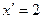 сумма
сумма 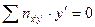 , для
, для 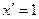 сумма
сумма 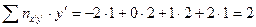 и т.д. Пятая строка (
и т.д. Пятая строка ( 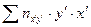 ) получена перемножением предыдущей строки на соответствующий интервал
) получена перемножением предыдущей строки на соответствующий интервал 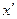 . Значения строки
. Значения строки 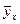 получены путем деления строки
получены путем деления строки 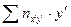 на значение строки
на значение строки 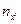 .
.
Пользуясь данными таблицы 3, по приведенным выше формулам вычислим последовательно статистические характеристики 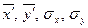 :
:
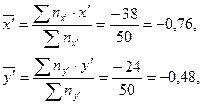

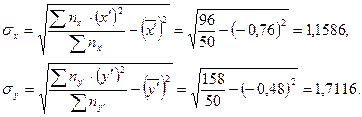
Коэффициент ковариации
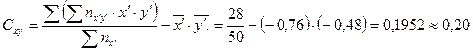
Вычисленные характеристики перенесем в первоначальную систему отсчета:
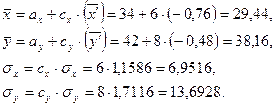
Подставив полученные значения величин в уравнение регрессии, получим значение коэффициента корреляции:
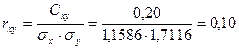
Вычислим корреляционное отношение 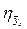 . Предварительно вычислим величину
. Предварительно вычислим величину 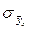 с помощью таблицы 4.
с помощью таблицы 4.
Таблица 4
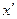 | 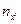 | 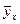 | 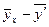 | 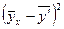 | 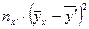 |
| -3 | -1,5 | -1,02 | 1,0404 | 2,0808 | |
| -2 | 0,48 | 0,2304 | 2,5344 | ||
| -1 | -1,21 | -0,73 | 0,5329 | 10,1251 | |
| 0,18 | 0,66 | 0,4356 | 4,7916 | ||
| 0,33 | 0,81 | 0,6561 | 3,9366 | ||
| 0,48 | 0,2304 | ||||
| -2 | -1,52 | 2,3104 | 2,3104 | ||
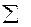 | 25,7789 |
Вычислим 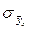 - СКО частной средней
- СКО частной средней 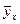 от общей средней
от общей средней 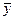 :
:
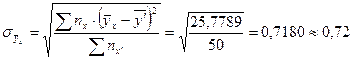
Тогда корреляционное отношение равно
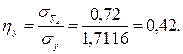
4. Проверка гипотезы равенства коэффициента корреляции корреляционному отношению и вывод уравнения регрессии.
Если коэффициент корреляции по абсолютной величине равен корреляционному отношению, то между переменными существует только линейная связь. Практически между 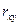 и
и 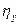 всегда будет различие. Для оценки существенности расхождения между ними применяют следующий метод.
всегда будет различие. Для оценки существенности расхождения между ними применяют следующий метод.
Определяется величина 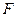 - критерий согласия Фишера:
- критерий согласия Фишера:
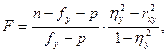
где 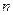 - объем выборки (
- объем выборки ( 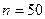 ),
),
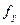 - число интервалов признака
- число интервалов признака 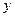 в корреляционной таблице (
в корреляционной таблице ( 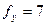 ),
),
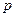 - число определяемых параметров в уравнении регрессии (для линейной зависимости
- число определяемых параметров в уравнении регрессии (для линейной зависимости 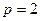 ).
).
Рассчитанное по формуле значение 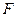 сравнивается с табличным
сравнивается с табличным 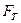 , которое, в свою очередь, выбирается в зависимости от числа степеней свободы
, которое, в свою очередь, выбирается в зависимости от числа степеней свободы 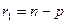 и
и 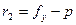 . Если
. Если 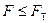 , то можно считать, что между
, то можно считать, что между 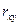 и
и 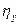 существует зависимость
существует зависимость 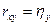 . Следовательно, зависимость между исследуемыми переменными точно линейная.
. Следовательно, зависимость между исследуемыми переменными точно линейная.
Определим величину 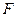 :
:
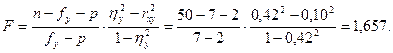
Для 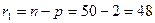 и
и 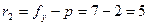 из таблицы критерия Фишера
из таблицы критерия Фишера 
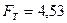 .
.
Так как 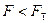 , то можно считать, что
, то можно считать, что 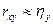 , то есть зависимость между исследуемыми параметрами точно линейная и может быть записана:
, то есть зависимость между исследуемыми параметрами точно линейная и может быть записана:
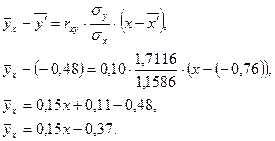
Полученное уравнение описывает влияние колебания длины общей нормали после зубофрезерования  на колебание длины общей нормали после шевингования-прикатывания
на колебание длины общей нормали после шевингования-прикатывания 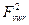 .
.
5. Анализ модели.
5.1 Проверка адекватности модели.
После вывода уравнения регрессии необходимо оценить его пригодность, т.е. нужно ответить на вопрос, можно ли с помощью полученной модели прогнозировать изменение выходного параметра в зависимости от поведения входного. Такая проверка модели называется «проверкой адекватности модели». Для раскрытия смысла этой проверки дадим графическую интерпретацию результатов эксперимента. Построим корреляционное поле.
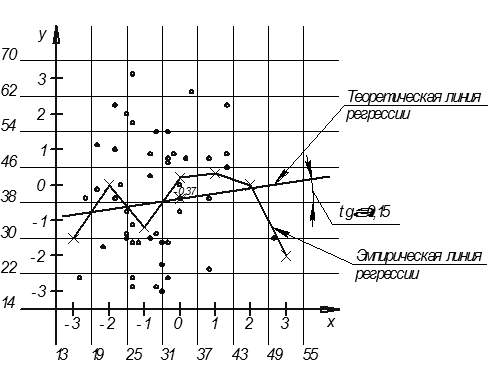
На корреляционном поле число точек в каждой клетке соответствует значению частот, указанных в таблице 2. По данным этой же таблицы на рисунке нанесены также точки, соответствующие значениям частных средних  в каждом интервале. Соединив эти точки отрезками, получим эмпирическую линию регрессии, а по уравнению регрессии
в каждом интервале. Соединив эти точки отрезками, получим эмпирическую линию регрессии, а по уравнению регрессии 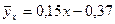 построим теоретическую линию регрессии.
построим теоретическую линию регрессии.
Оценка адекватности модели заключается в сравнении общей дисперсии исследуемого признака с дисперсией, обусловленной полученным уравнением регрессии и характеризующей отклонение эмпирической линии регрессии от теоретической.
Для сравнения дисперсий используется критерий Фишера 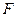 . Модель можно считать адекватной, если вычисленное значение
. Модель можно считать адекватной, если вычисленное значение 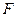 будет меньше табличного.
будет меньше табличного.
Оценим адекватность уравнения регрессии
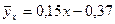 .
.
Чтобы оценить адекватность данной модели, необходимо знать общую и межинтервальную дисперсии.
По данным примера общая дисперсия
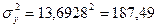
Для расчета межинтервальной дисперсии составим таблицу 5.
Таблица 5
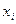  | 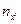 | 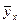 | 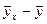 | 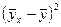 | 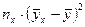 |
| 2,03 | -36,13 | 1305,3769 | 2610,7538 | ||
| 2,93 | -35,23 | 1241,1529 | 13652,6819 | ||
| 3,83 | -34,33 | 1178,5489 | 22392,4291 | ||
| 4,73 | -33,43 | 1117,5649 | 12293,2139 | ||
| 5,63 | -32,53 | 1058,2009 | 6349,2054 | ||
| 6,53 | -31,63 | 1000,4569 | |||
| 7,43 | -30,73 | 944,3329 | 944,3329 | ||
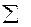 | 58242,617 |
Значения графы 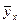 получены путем подстановки соответствующих значений
получены путем подстановки соответствующих значений 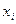 в уравнение регрессии
в уравнение регрессии 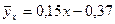 .
.
Подсчитав сумму последней графы, определим
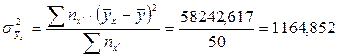
Тогда расчетное значение критерия Фишера
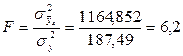
При этом табличное значение 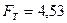 . Т.к.
. Т.к. 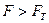 , можно сделать вывод, что полученная модель неадекватна, т.е. с помощью уравнения регрессии нельзя прогнозировать колебание длины общей нормали после чистовой операции шевингования-прокатывания в зависимости от полученного значения колебания длины общей нормали после предварительной обработки зубофрезерования.
, можно сделать вывод, что полученная модель неадекватна, т.е. с помощью уравнения регрессии нельзя прогнозировать колебание длины общей нормали после чистовой операции шевингования-прокатывания в зависимости от полученного значения колебания длины общей нормали после предварительной обработки зубофрезерования.
5.2 Оценка значимости коэффициента корреляции.
Приближенный метод
Если в результате обработки результатов эксперимента получено небольшое значение 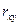 , возникает вопрос, не случайно ли значение
, возникает вопрос, не случайно ли значение 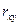 значимо отличается от нуля.
значимо отличается от нуля.
Можно считать, что 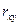 значимо отличается от нуля и связь между исследуемыми факторами реальна, если выполняется условие
значимо отличается от нуля и связь между исследуемыми факторами реальна, если выполняется условие
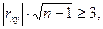
где 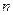 - число опытов.
- число опытов.
В противном случае прямолинейная корреляционная связь не обнаруживается.
Оценим значимость коэффициента корреляции при 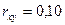 и
и 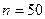 :
:
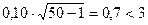 .
.
Следовательно, величина коэффициента корреляции незначима, т.е. связь между факторами отсутствует.
Уточненный метод
Приближенный метод может оказаться недостаточным при небольшом числе наблюдений (обычно при 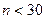 ). В этом случае для оценки значимости коэффициента корреляции предварительно вычисляется
). В этом случае для оценки значимости коэффициента корреляции предварительно вычисляется 
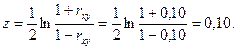
Рассеяние параметра 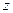
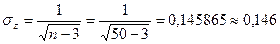
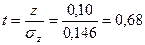
Полученное значение 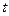 сравнивается с табличным, которое выбирается в зависимости от числа степеней свободы
сравнивается с табличным, которое выбирается в зависимости от числа степеней свободы 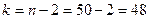 и уровня доверительной вероятности
и уровня доверительной вероятности 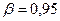 :
:
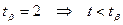 .
.
Значит, условие значимости коэффициента корреляции не выполнено. Следовательно, корреляционная связь между параметрами отсутствует.
5.3 Построение доверительных границ для линии регрессии.
Статистические характеристики, полученные в результате обработки экспериментальных данных, являются оценками теоретических параметров, а не самими теоретическими параметрами. Например,
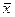 - оценка математического ожидания
- оценка математического ожидания 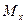 ,
,
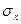 - оценка дисперсии
- оценка дисперсии 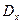 .
.
Уравнение регрессии 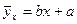 является оценочным по отношению к теоретическому уравнению
является оценочным по отношению к теоретическому уравнению 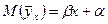 , которое точно установить нельзя, но можно построить доверительную область, в которой лежит линия истинной регрессии. Чтобы построить эту область, определим доверительные границы для математического ожидания исследуемой выходной величины
, которое точно установить нельзя, но можно построить доверительную область, в которой лежит линия истинной регрессии. Чтобы построить эту область, определим доверительные границы для математического ожидания исследуемой выходной величины 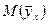 и теоретического коэффициента регрессии
и теоретического коэффициента регрессии 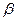 .
.
Доверительные границы для математического ожидания исследуемой выходной величины 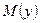 :
:
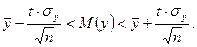
Для коэффициента регрессии доверительные границы можно определить с помощью неравенства:
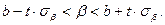
Рассмотрим методику построения доверительной области для теоретической линии регрессии 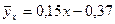 .
.
Величину 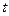 найдем с помощью функции Лапласа. Для этого зададимся доверительной вероятностью
найдем с помощью функции Лапласа. Для этого зададимся доверительной вероятностью 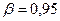 . Исходя их соотношения, что
. Исходя их соотношения, что 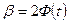 , по таблице найдем
, по таблице найдем 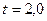 . Вычислим величину
. Вычислим величину
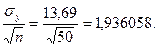
Следовательно, доверительные границы для математического ожидания исследуемой выходной величины  :
:
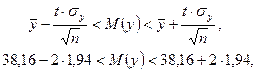
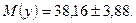
Чтобы найти доверительные границы коэффициента регрессии 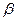 , вычислим СКО
, вычислим СКО
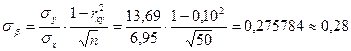
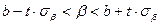

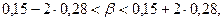
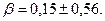
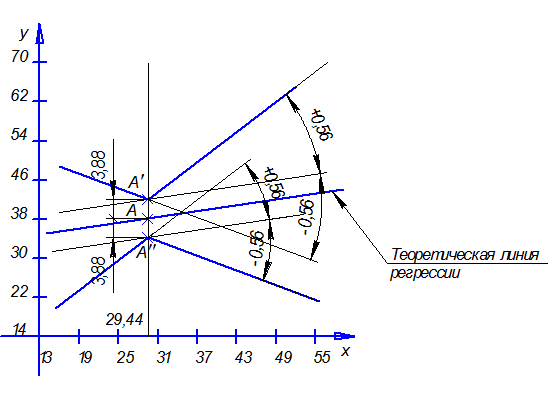
Порядок построения доверительных границ следующий. Сначала на график наносится точка 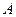 с координатами
с координатами 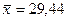 и
и 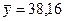 , затем точки
, затем точки 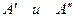 с координатами
с координатами 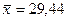 и
и 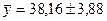 . Через точку
. Через точку 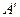 проводятся две линии, тангенс угла которых
проводятся две линии, тангенс угла которых 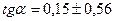 . Тем же образом проводятся две линии и через точку
. Тем же образом проводятся две линии и через точку  . Ломаные, проведенные через
. Ломаные, проведенные через  , ограничивают область доверительных границ истинной линии регрессии.
, ограничивают область доверительных границ истинной линии регрессии.
5.4 Дисперсионный анализ результатов моделирования.
Количественную оценку влияния точности предварительной обработки на точность окончательной обработки можно установить с помощью дисперсионного анализа.
Отклонения точек корреляционного поля от линии регрессии 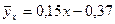 можно оценить величиной дисперсии
можно оценить величиной дисперсии 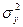 , которую представляют в виде суммы двух дисперсий:
, которую представляют в виде суммы двух дисперсий:
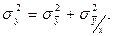
Первая из них 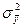 является количественной оценкой величины отклонения точек, представляющих собой конкретные значения величины отдельных деталей
является количественной оценкой величины отклонения точек, представляющих собой конкретные значения величины отдельных деталей 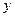 , от эмпирической линии регрессии. Дисперсия
, от эмпирической линии регрессии. Дисперсия 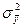 есть следствие влияния
есть следствие влияния 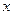 на
на 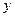 .
.
Наличие дисперсии 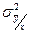 объясняется тем, что на выходной параметр
объясняется тем, что на выходной параметр 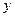 кроме фактора
кроме фактора 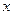 влияют и другие факторы, которые не были учтены в модели.
влияют и другие факторы, которые не были учтены в модели.
Первое и второе слагаемые правой части уравнения определяются по формулам:
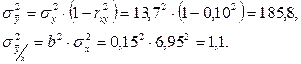
Тогда
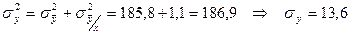
Таким образом, формула позволяет проверить рассчитанную ранее дисперсию 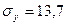 .
.
Приняв 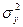 за 100 % , получим
за 100 % , получим
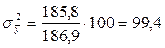 %
%
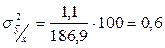 %
%
На основе дисперсионного анализа можно сделать следующий вывод: на величину выходного параметра окажет влияние входной параметр на 99,4% и на 0,6% факторы, которые не учтены в модели.
Общие выводы по заданию:
1. Установлено, что между величинами 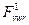 и
и 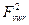 отсутствует корреляционная связь.
отсутствует корреляционная связь.
2. Проверка адекватности модели показала невозможность прогнозирования значения выходного параметра по величине входного.
3. Дисперсионный анализ позволил не только качественно, но и количественно оценить степень влияния входной величины на выходную.
ЗАДАНИЕ 4
ЗАДЩАНИЕ 5
ЗАДАНИЕ 6
Множественная корреляция
Корреляционные связи могут существовать не только между двумя, но и между несколькими признаками. Например, овальность после чистового шлифования зависит от припуска на чистовое шлифование и от овальности после предварительного шлифования. Припуск на шлифование зубьев зависит от величины деформации заготовок шестерен после термической обработки и от погрешности обработки, полученной после зубонарезания.
Исследование статистических связей между многими величинами является предметом теории множественной корреляции. В практике механической обработки деталей на металлорежущих станках чаще всего встречаются случаи линейной корреляционной связи между тремя величинами или тремя факторами.
Рассмотрим простейший случай линейной корреляционной связи между тремя величинами 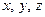 . Причем будем считать
. Причем будем считать 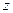 - величиной, зависящей от
- величиной, зависящей от 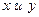 . Линейную корреляционную связь между этими величинами можно записать в виде уравнения:
. Линейную корреляционную связь между этими величинами можно записать в виде уравнения:
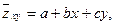
где 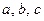 - постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между
- постоянные коэффициенты, которые вычисляются с помощью коэффициентов корреляции между 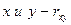 , между
, между 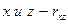 , между
, между 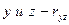 , а также СКО
, а также СКО 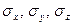 по формулам:
по формулам:
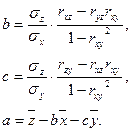
Мерой силы линейной связи между  в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом:
в совокупности служит коэффициент множественной корреляции или сводный коэффициент корреляции, который вычисляется следующим образом:
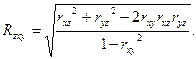
Примечание: коэффициент 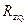 всегда положителен, его значение лежит в пределах от 0 до +1. Если
всегда положителен, его значение лежит в пределах от 0 до +1. Если 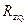 равен 0, то
равен 0, то 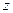 не имеет линейной связи с
не имеет линейной связи с 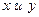 , но возможна криволинейная связь. Если
, но возможна криволинейная связь. Если 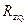 равен 1, то между
равен 1, то между 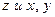 существует точно линейная связь вида
существует точно линейная связь вида 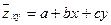 .
.
Для исследования наличия связи между 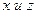 ,
, 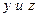 , а также для оценки влияния
, а также для оценки влияния 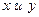 в отдельности на
в отдельности на 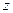 пользуются частными коэффициентами, которые обозначаются
пользуются частными коэффициентами, которые обозначаются
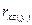 - связь между
- связь между 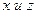 при постоянном значении
при постоянном значении 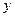 ,
,
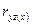 - связь между
- связь между 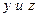 при постоянном значении
при постоянном значении 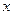 .
.
Эти коэффициенты вычисляются по формулам:
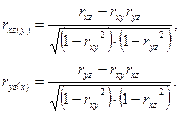
Смысл частных коэффициентов заключается в том, что они служат мерой линейной с
